题目

思路

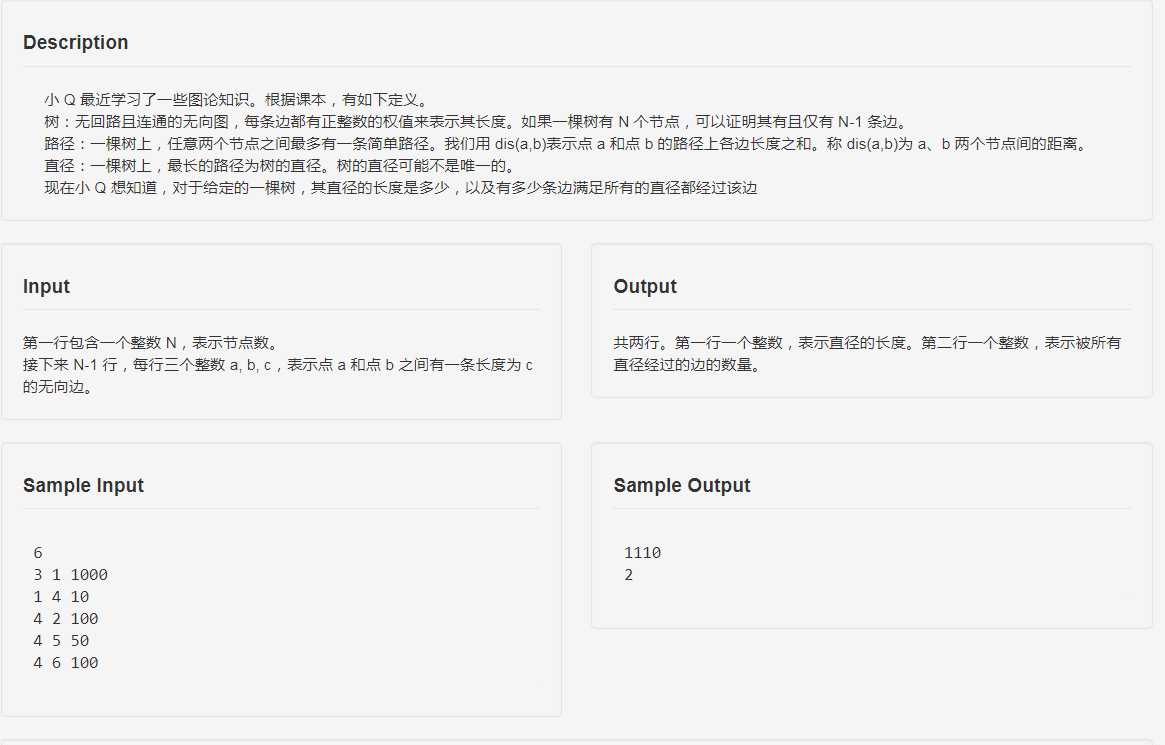
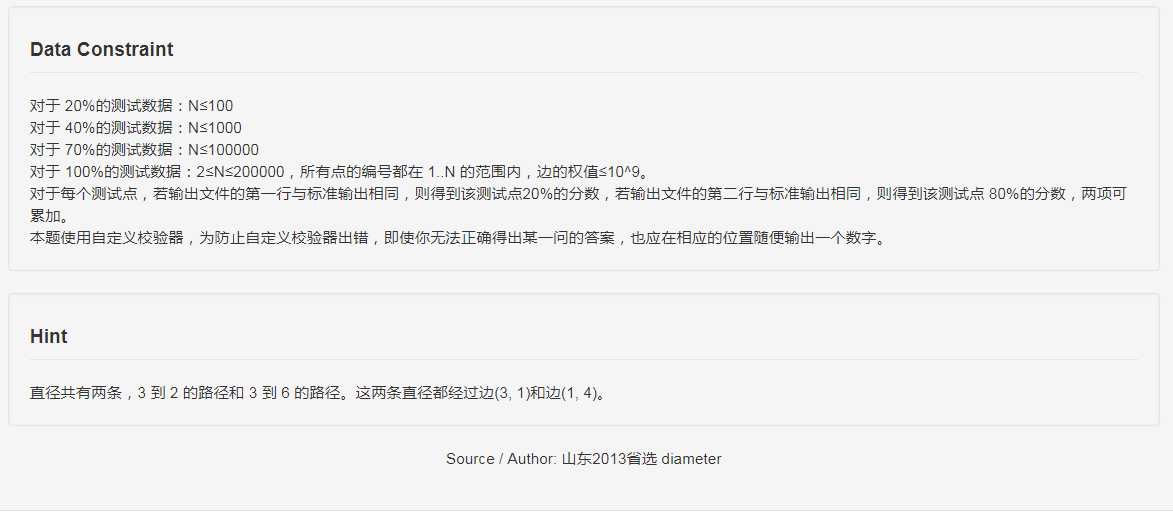
树的直径很好求，两遍 \(dfs\)，记下两个端点
然后很显然所有直径经过的边必然在我们求出的这条直线上
那么我们只要判断一下一条直径上的边是不是答案
假设当前边为 \(i\)
那么把 \(i\) 割去后原树变成了两棵不联通的树
我们只要看这两棵子树分别的直径和不和原树的直径相等
如果至少有一条相等，那么说明原树中有一条直径可以不经过 \(i\)
故这种 \(i\) 不是答案
那么我们对直径一端到另一端的边依次判断即可
如何快速求分开后子树的直径？
我们可以 \(dfs\) 出分别以直径两端为根的每个节点的最长链，次长链以及本节点子树中的直径
转移就很好办了

\(Code\)

#include<cstdio>
#include<algorithm>
#include<iostream>
using namespace std;
typedef long long LL;

const int N = 2e5 + 5;
int n , h[N] , tot , p , q , pre[N];
LL dis , f1[N] , f2[N] , f3[N] , g1[N] , g2[N] , g3[N] , s , ss;

struct edge{
	int to , nxt , w;
}e[N << 1];

inline void add(int x , int y , int z)
{
	e[++tot] = (edge){y , h[x] , z};
	h[x] = tot;
}

inline void dfs(int x , int fa , LL d)
{
	if (d > dis) dis = d , q = x;
	for(register int i = h[x]; i; i = e[i].nxt)
	{
		int v = e[i].to;
		if (v == fa) continue;
		dfs(v , x , d + e[i].w);
	}
}

inline void dfs1(int x , int fa , LL d)
{
	pre[x] = fa;
	if (d > dis) dis = d , q = x;
	for(register int i = h[x]; i; i = e[i].nxt)
	{
		int v = e[i].to;
		if (v == fa) continue;
		dfs1(v , x , d + e[i].w);
		if (f1[v] + e[i].w > f1[x]) f2[x] = f1[x] , f1[x] = f1[v] + e[i].w;
		else if (f1[v] + e[i].w > f2[x]) f2[x] = f1[v] + e[i].w;
		f3[x] = max(f3[x] , f3[v]);
	}
	f3[x] = max(f3[x] , f1[x] + f2[x]);
}

inline void dfs2(int x , int fa)
{
	for(register int i = h[x]; i; i = e[i].nxt)
	{
		int v = e[i].to;
		if (v == fa) continue;
		dfs2(v , x);
		if (g1[v] + e[i].w > g1[x]) g2[x] = g1[x] , g1[x] = g1[v] + e[i].w;
		else if (g1[v] + e[i].w > g2[x]) g2[x] = g1[v] + e[i].w;
		g3[x] = max(g3[x] , g3[v]);
	}
	g3[x] = max(g3[x] , g1[x] + g2[x]);
}

inline void work()
{
	dis = 0;
	dfs(1 , 0 , 0);
	p = q;
	dis = 0;
	dfs1(p , 0 , 0);
	dfs2(q , 0);
	
	for(register int i = q; i != p; i = pre[i])
	{
		s++;
		if (f3[i] == dis || g3[pre[i]] == dis) ss++;
	}
	printf("%lld\n%lld" , dis , s - ss);
}

int main()
{
	scanf("%d" , &n);
	int u , v , w;
	for(register int i = 1; i < n; i++) 
	{
		scanf("%d%d%d" , &u , &v , &w);
		add(u , v , w) , add(v , u , w);
	}
	work();
}

JZOJ 3213. 【SDOI2013】直径

原文：https://www.cnblogs.com/leiyuanze/p/13427208.html