1.1概述

并查集是一种树形的数据结构，用于处理不交集的合并(union)及查询(find)问题。并查集可用于查询网络中两个节点的状态， 这里的网络是一个抽象的概念， 不仅仅指互联网中的网络， 也可以是人际关系的网络、交通网络等。

1.2详解

并查集的重要思想在于，用集合中的一个元素代表集合。我曾看过一个有趣的比喻，把集合比喻成帮派，而代表元素则是帮主。接下来我们利用这个比喻，看看并查集是如何运作的。
首先每个人都各自为阵：

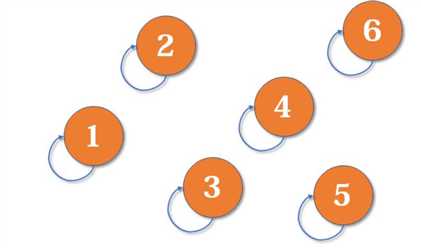
然后根据情况对其中的集合进行合并：也就是指向一个集合的代表。

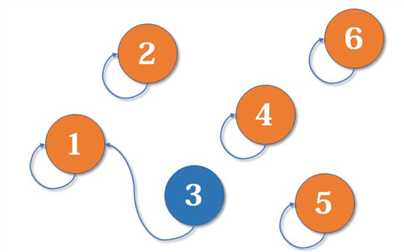
上面步骤就是并查集的合并操作，另外一个比较重要的操作就是查询操作，判断两个元素是否是同一个集合。

1.3代码

• 这里采用数组的形式实现并查集，其中值为-1代表该元素为集合代表，其他则代表该元素所处集合的代表坐标。
• 这里实现的只是最简单的版本，其中元素只能为正整数（也就是数组的下标）。拓展版本可以借助map集合实现下标和元素的映射关系。
• 其实还可以进行优化操作，这里的版本很明显最后生成的结构是一棵树，假如运气不好，所有节点都在上一个节点的同一侧，就退化成了链表形式了。所以可以增加一个rank数组来记录树的高度，合并的时候作为判断依据避免树退化成链表。也可以将所有节点都直接指向root节点，这样就是棵n叉树，只有两层。

package disjointset;

import java.util.Arrays;

/**
 * JavaTest
 *
 * @author : xgj
 * @description : 并查集简单实现
 * @date : 2020-08-05 20:43
 **/
public class DisjointSet {
    /**
     * 底层数组
     */
    private int[] parent;
    /**
     *并查集的元素个数
     */
    private int size;
    /**
     *功能描述 : 初始化，元素指向-1
     *
     * @author xgj
     * @date 2020/8/5
     */
    public DisjointSet(int size) {
        //初始化个数
        this.size = size;
        //初始化数组，每个并查集都指向自己
        parent = new int[size];
        Arrays.fill(parent,-1);
    }
    /**
     *功能描述 : 找到父节点
     *
     * @author xgj
     * @date 2020/8/5
     */
    private int find(int element) {
        if(element > size || element < 0){
            System.out.println("范围错误");
        }
        if(parent[element] == -1) {
            return element;
        }
        return find(parent[element]);
    }
    /**
     *功能描述 : 查询是否属于一组
     *
     * @author xgj
     * @date 2020/8/5
     * @param element1
     * @param element2
     * @return boolean
     */
    public boolean isConnected(int element1 ,int element2){
        int parent1 = find(element1);
        int parent2 = find(element2);
        return parent1 == parent2;
    }
    /**
     *功能描述 : 合并两个元素所在集合
     *
     * @author xgj
     * @date 2020/8/5
     * @param element1
     * @param element2
     * @return boolean
     */
    public boolean unionElements(int element1,int element2){
        int parent1 = find(element1);
        int parent2 = find(element2);
        if(parent1 == parent2) {
            return false;
        }
        parent[parent1] = parent2;
        return true;
    }
    /**
     *功能描述 : 输出并查集
     *
     * @author xgj
     * @date 2020/8/5
     * @param
     * @return void
     */
    public void printArr(){
        System.out.println(Arrays.toString(parent));
    }
}

DisjointSet并查集

原文：https://www.cnblogs.com/jiezao/p/13445823.html