基于未知准则的WSS失效异常检测算法
——第二种算法LOF算法(异常离群算法—非聚类算法)
1.算法原理介绍
LOF算法,全称是Local Outlier Factor(局部离群因子检测方法),是一种基于密度的高精度离群点异常检测算法。基于密度的离群点检测方法的关键步骤在于给每个数据点都分配一个离散度,其主要思想是:针对给定的数据集,对其中的任意一个数据点,如果在其局部邻域内的点都很密集,那么认为此数据点为正常数据点,而离群点则是距离正常数据点最近邻的点都比较远的数据点,通常有阈值进行界定距离的远近。
LOF算法具体是通过给每个数据点都计算出一个依赖于邻域密度的离群因子 LOF,通过计算出每一个点的离群因子大小进而判断该数据点是否为离群点。若 LOF >> 1, 则该数据点为异常离群点类型;若 LOF 接近于 1,则该数据点为正常数据点类型。
2.算法适用情况
LOF算法的思想是利用算法将特征分布异常离群的点“挑出来”,而不是像非监督聚类算法一样把异常分布相似的点集“聚出来”,其核心是将数据分布密度较小,分布比较零散异常数据检测出来。所以,当未知类型的异常数据因为各种原因而分布比较零散,并且距离正常数据集合较远时,LOF算法具有很好的表现性能,这是由其本身的算法原理所决定的。
3.算法计算中一些概念
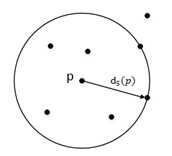
(1)K距离:
对于数据集合的任何一个点O,计算它与其他点的距离,并对其进行从小到大排序,第k个即为该点的k距离。
(2)k距离邻域:
k距离邻域是指到点O的距离小于等于k距离的点的集合,共k个,即到点O最近的k个点的集合(不是指一个空间邻域,而是指一个点集)。
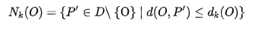
(3)可达距离:
若任何其他一点P到点O的实际距离小于k距离,则将可达距离定义为k距离,反之可达距离为点P到点O的实际距离大小
(4)局部可达密度lrd:
K距离邻域内所有点Pi到O点的可达距离平均值的倒数。
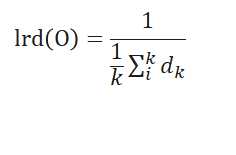
(5)局部离群因子lof:
K距离领域内所有点Pi的局部可达密度的均值除以O点的局部可达密度。
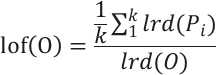
局部离群因子大小越大,该点越可能是离群点。
具体来说,如果比值(局部离群因子)越接近1,说明邻域内点的密度差不多,可能和邻域是同属一簇,属于正常点;如果这比值小于1,说明该点处的密度高于其邻域点的密度,属于为密集点;如果这个比值远大于1,说明该点处的密度远小于其邻域点密度,很有可能是异常分布点。
4.算法核心思想
总结来讲,LOF算法主要是通过比较每个点和其邻域点的密度来判断该点是否为异常点,如果点的密度越低,越可能被认定是异常点。至于密度,是通过点之间的距离来计算的,点之间距离越远,密度越低,距离越近,密度越高。而且,因为LOF对密度的是通过点的第k邻域来计算,而不是全局计算,因此LOF算法不会因为数据密度分散情况不同而错误的将正常点判定为异常点。具有很高的离群异常检测精度。
5.算法的具体步骤:
(1)指定离群异常检测算法的k值大小和离群因子大小判断的阈值大小epsilon;
(2)结合指定k值,计算出每一个原始数据的局部离群因子大小大小;
(3)输出局部离群因子大于1的点,即判读为异常点,小于1的点判断输出为正常点。
需要说明的是,整体LOF算法的具体检测性能表现与邻阈大小k值和局部密度判断的阈值epsilon密切相关,不同的k值和epsilon阈值,LOF算法的性能表现是不一样的,所以LOF算法在实际异常数据检测中,需要根据具体业务背景和实际数据分布特点来进行k值和epsilon的大小设定。
6.算法性能测试:
(1)仿真数据测试:
首先使用仿真数据进行LOF算法的验证和测试,如下为所有数据集的整体分布情况(以二维数据展示),两种不同的预计分布情况,此时异常数据未知
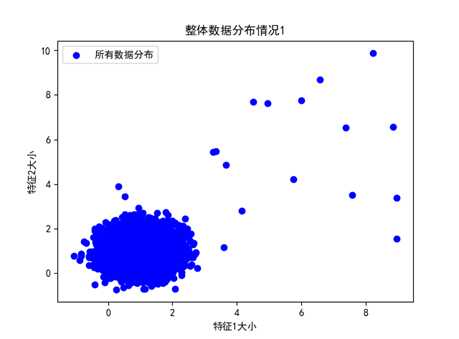
图 整体数据分布情况1(异常数据20个)
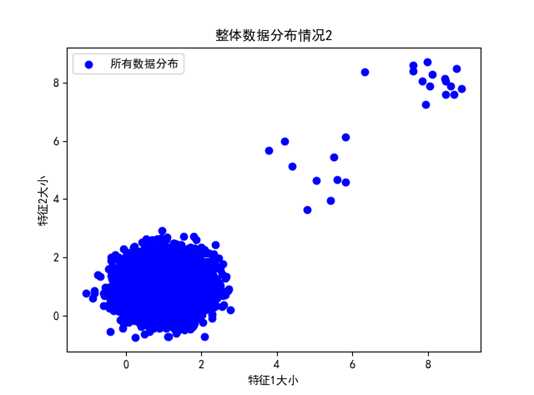
图 整体数据分布情况2(异常数据25个)
第一,设定不同的算法k值(epsilon阈值保持不变,默认设置为2),测试其算法对不同数据集异常预测的结果,不同的k值其最终的结果分别如下图所示:
① k=5时:
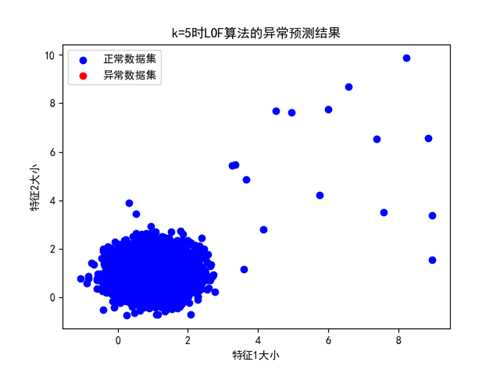
图 k=5时的LOF异常预测结果展示(数据分布情况1,未检测出)
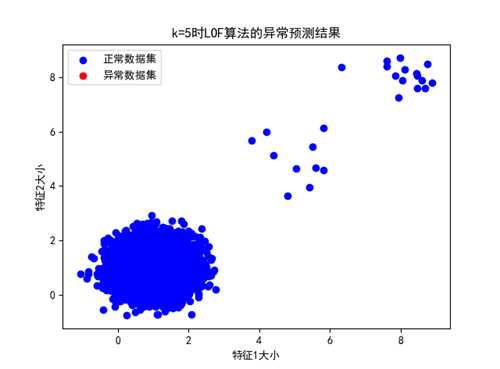
图 k=5时的LOF异常预测结果展示(数据分布情况2,未检测出)
K=5时,因为正常数据和异常数据的局部数据密度均较大,而k的值太小,所以LOF算法不能够直接检测出异常的数据集合。
② k=20时
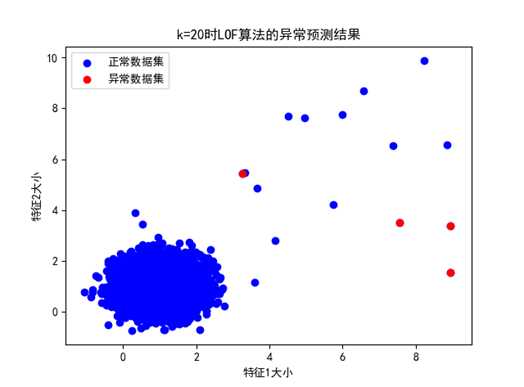
图 k=20时的LOF异常预测结果展示(数据分布情况1,准确率为25%)
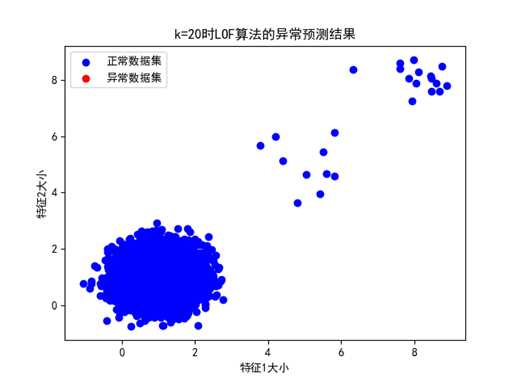
图 k=20时的LOF异常预测结果展示(数据分布情况2,未检测出)
K=20时,可以看到LOF算法对于局部分布比较零散的部分异常数据做出了预测,而对于异常数据分布局部集群密度较大的情况检测不出。
③ k=50时:
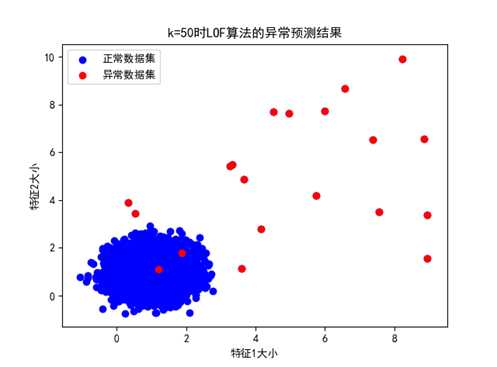
图 k=50时的LOF异常预测结果展示(数据分布情况1,准确率100%)
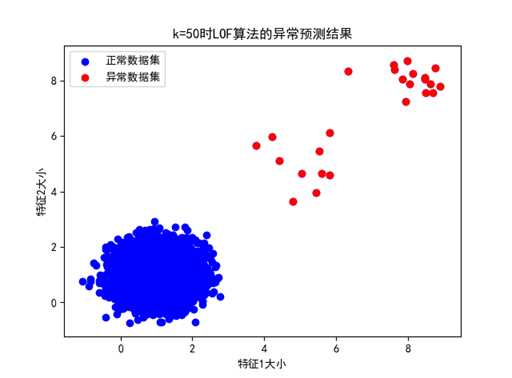
图 k=50时的LOF异常预测结果展示(数据分布情况2,准确率100%)
k=50时,可以看到对于两种不同情况的数据分布,LOF均可以将其检测出来,准确率达到了100%,这是因为k的值均高于了异常值的分布个数。
④ k=100时:
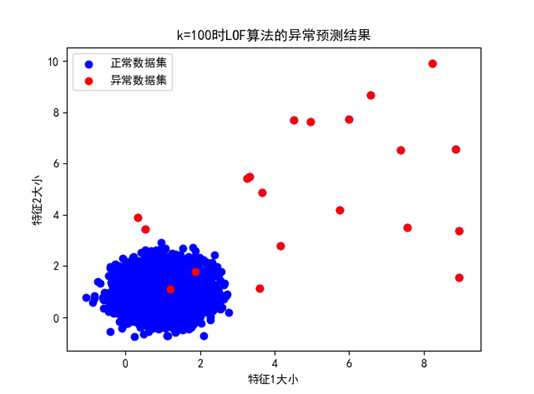
图 k值为100时分类结果(分布情况1,准确率100%)
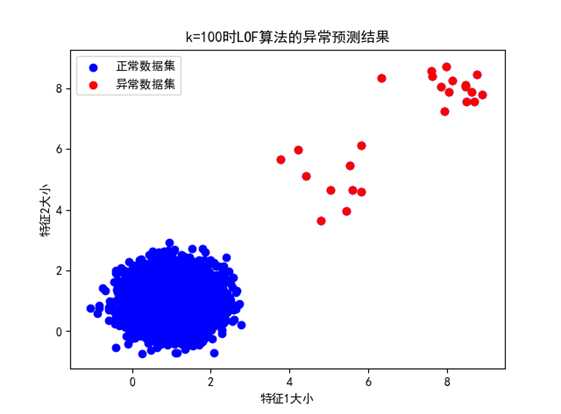
图 k值为100时分类结果(分布情况2,准确率为100%)
可以看到,k=100时,LOF算法也可以将两种情况的异常数据检测出来,准确率依旧为100%;所以,当k达到一定的阈值时,LOF算法的准确率会基本保持不变。
第二,参数epsilon对于异常预测结果的具体影响(保持邻域参数k不变,设置为50)
① Epsilon=1时,异常预测的结果如下所示:
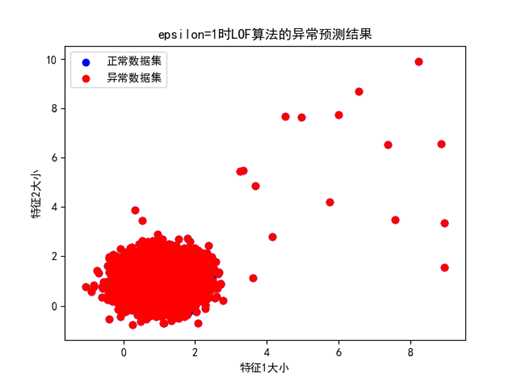
图 epsilon=1时的异常预测预测结果
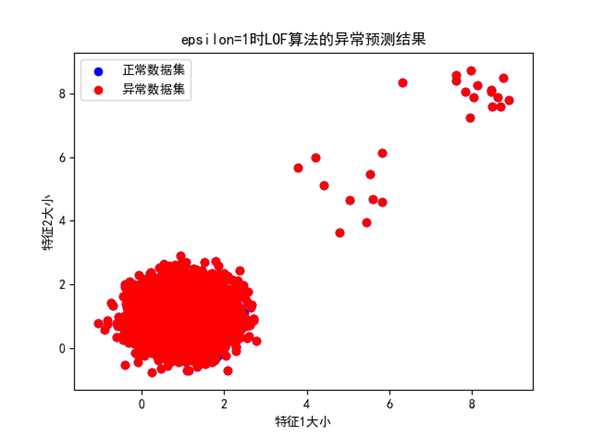
图 epsilon=1时的异常预测预测结果
可以看出,epsilon=1时异常检测将非常多的点误判为了异常点,主要是因为epsilon值太接近于1,使得很多正常点中局部密度较小的点也被判断为了异常点。
② Epsilon=2:
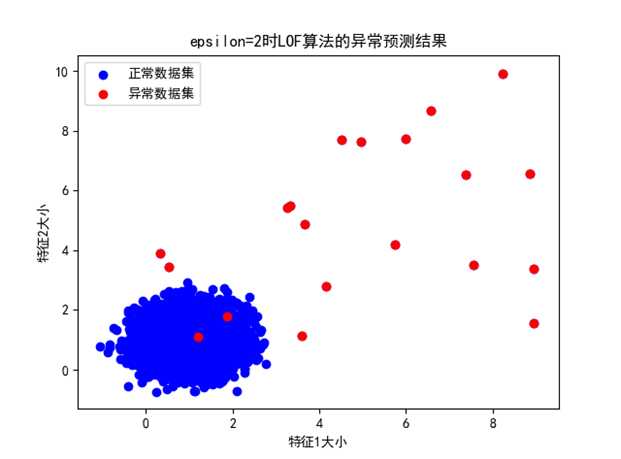
图 epsilon=2时的异常预测预测结果
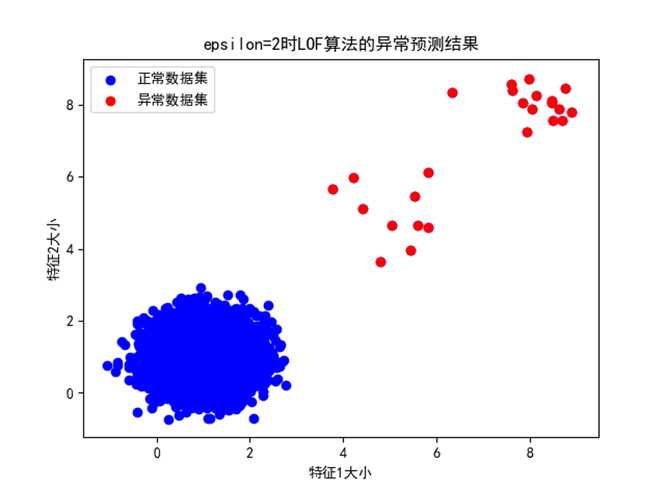
图 epsilon=2时的异常预测预测结果
可以看出,epsilon=2时LOF算法将两种情况下的异常点非常准确的预测出来。
③ Epsilon=5时:
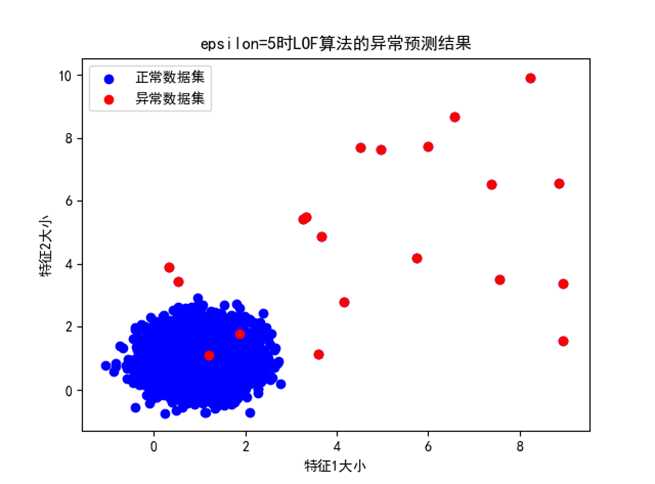
图 epsilon=5时异常预测的结果
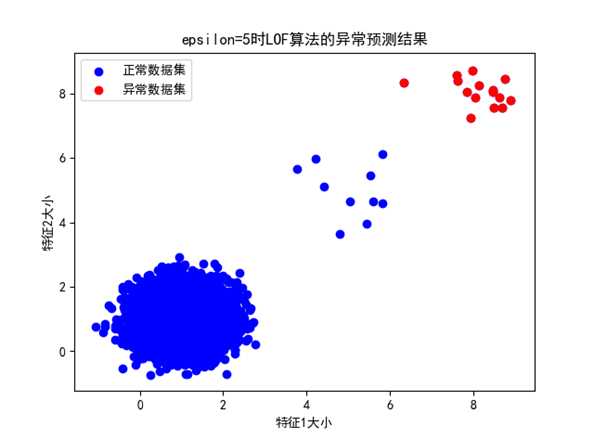
图 epsilon=5时异常预测的结果
可以看出,epsilon=5时,LOF算法异常检测的结果在数据分布1的情况下是准确的,但是在多个分布集群时,只预测出了异常数据的一部分,主要是因为epsilon太大,导致密度判断条件太严格造成的。此时,整体检测的准确率很高,但是召回率较低。
最终,基于以上的测试结果与分析,可以得到如下的几个结论:
第一,不同的k值和epsilon值的选择,其算法的异常预测结果是不一样的,两者的大小将直接影响LOF算法在面对不同原始数据集时的精度表现。
第二,k值太小,LOF算法会漏检一些异常的数据,也会错检一些正常数据,即准确率和召回率都比较小,随着k值的不断增大,其异常预测的结果趋于更加合理,准确率和召回率均会慢慢增大,但是k太大,会使得LOF算法的运行效率越来越慢,原因是需要计算的各个点的邻域越来越大,算法的计算量也随之增大。另外,为了保证算法的预测精度,k值大小不能小于原始数据集中异常数据的总数。
第三,epsilon值太小,会使得LOF算法的准确率很低,但召回率很高,随着epsilon值的增大,算法的准确率在不断的增大,召回率会不断下降。因此,为了兼顾LOF算法的准确率和召回率,epsilon值的大小设置不能太大,也不能太小,一般可以设置为2左右。
(2)真实数据算法测试
使用真实数据进行测试(设置k为50,epsilon为2):
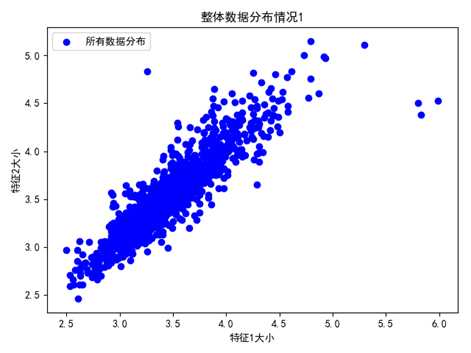
图 原始数据分布(仅展示数据的前两个特征)
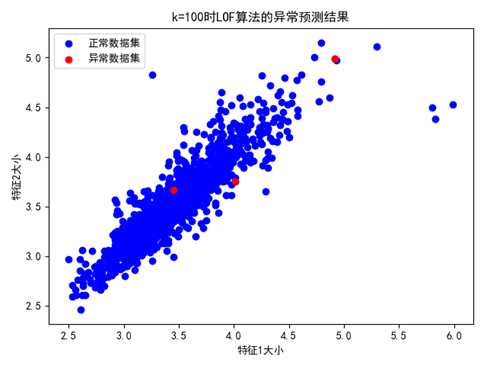
图 LOF算法的异常检测结果(仅展示数据的前两个特征)
LOF算法检测出了三个异常点:
831:[3.45 3.67 3.49 3.53 3.55 4.21 7.08 3.36 3.47 3.63 3.58 3.71 3.7 3.62 3.58 3.59 3.68 4.92 3.95 5.01 4.85 4.7 4.23 3.04 3.23 3.12 3.07 3.03 3.21 6.79 3.1 3.08 3.3 3.29 3.37 3.36 3.3 3.15 3.27 3.3 3.71 3.45 3.47 3.88 3.87 3.88 3.18 3.41 3.29 3.26 3.2 3.42 7.02 3.17 3.22 3.38 3.44 3.51 3.52 3.45 3.32 3.43 3.46 3.84 3.62 3.62 4.04 4.04 4.04]
834:[4.01 3.75 6.95 3.65 7.5 3.36 3.43 3.44 3.58 3.56 3.47 3.32 3.83 3.56 3.75 3.72 3.79 4.19 3.96 4.13 4.29 3.8 4.38 3.66 3.45 6.76 3.36 7.3 3.29 3.24 3.26 3.41 3.38 3.31 3.23 3.76 3.5 3.66 3.69 3.69 3.83 3.89 3.88 4.34 4.19 4.29 3.68 3.43 6.81 3.39 7.37 3.28 3.21 3.25 3.36 3.36 3.25 3.24 3.7 3.43 3.62 3.62 3.64 3.74 3.82 3.8 4.31 4.08 4.11]
998:[4.92 4.99 4.85 5.11 5.23 4.03 4.87 4.78 4.93 4.85 4.88 4.82 4.77 5. 5.34 5.18 5.17 3.52 5.31 4.3 4.05 4.62 5.6 4.7 4.77 4.64 4.92 4.95 4.4 4.72 4.72 4.8 4.82 4.82 4.82 4.87 5.08 5.23 5.19 5.14 5.21 5.31 5.69 5.49 5.65 5.73 4.8 4.84 4.73 5.05 5.07 4.5 4.85 4.83 4.99 5.01 5.07 5.04 5.11 5.29 5.62 5.5 5.45 5.51 5.58 6.0 5.64 5.87 5.88]
所有预测异常的结果真实情况下也为异常,预测准确率为100%,但是召回率较低。
6. 总结:
LOF算法是一种基于局部密度大小的离群点异常检测算法,在WSS失效异常准则未知的情况下可以实现一定异常预测的功能,具有较好的性能表现。其中,算法的整体性能是由算法的k值和epsilon值共同决定的。另外,在一般情况下,LOF算法整体异常预测的准确率很高,但是很难将所有可能异常的数据检测出来,即算法的精准率较高,但召回率不会太高。
原文:https://www.cnblogs.com/Yanjy-OnlyOne/p/13447377.html