[Machine Learning] Evaluation Metrics

Evaluation Metrics are how you can tell if your machine learning algorithm is getting better and how well you are doing overall.

• Accuracy
• x
• x
• x

Accuracy:

The accuracy should actually be no. of all data points labeled correctly divided by all data points. 

Shortcome of max Accuracy:

• not ideal for skewed classses. (Skewed classes basically refer to a dataset, wherein the number of training example belonging to one class out-numbers heavily the number of training examples beloning to the other.)
• may want to error on side of guessing innocent (if you want to put someone into jail, you need to really make sure he is getting involved, if you have any doubt, you should assume him is innocent)
• may want to error on side of guessing gulity (Investigations are going on, you need to do is involved as many people in the fraud as possible, even if it comes to the cose of identifying some people who were innocent)

Confusion Materix:

A confusion matrix is a table that is often used to describe the performance of a classification model (or “classifier”) on a set of test data for which the true values are known. It allows the visualization of the performance of an algorithm.

Correct classfied:

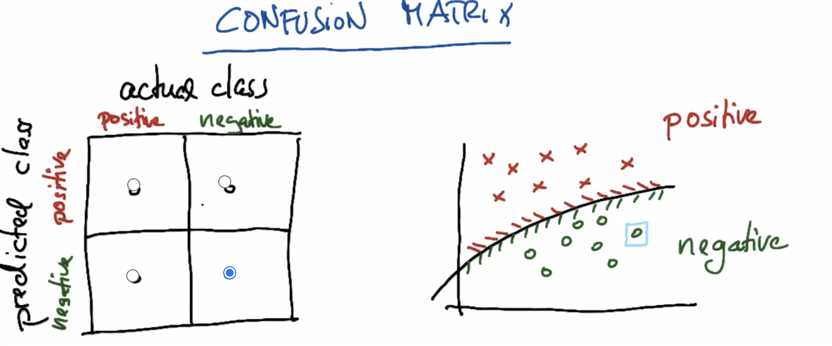
Wrong classfied:

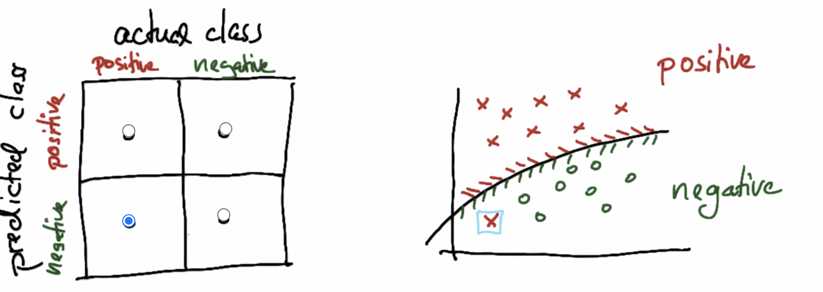
Count matrix:

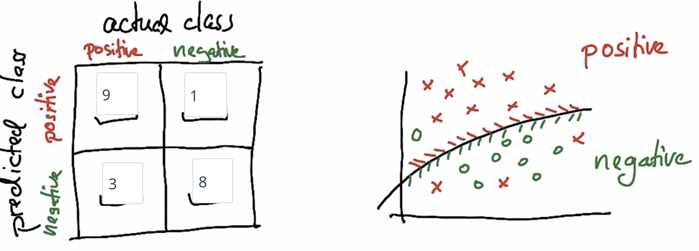
If we convert into a SVM:

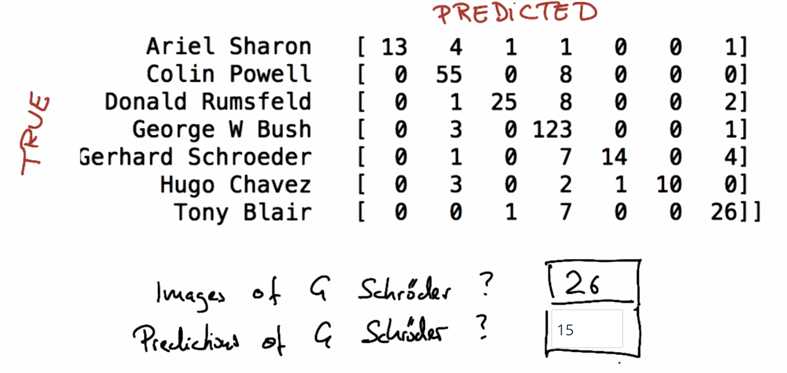
For the cross line, which has the largest number, is the ture predicted. Other parts are false predicated.

The sum of row = total image for one person

The sum of column = total predciction occurs for one person

For G. Schroeder: total predictions = 14 + 1 = 15.

Recall / Precision:

Recall: True Positive / (True Positive + False Negative). Out of all the items that are truly positive, how many were correctly classified as positive. Or simply, for the whole items for one label, how many % was correctly predicted

Precision: True Positive / (True Positive + False Positive). Out of all the items labeled as positive, how many truly belong to the positive class.

Easy way to remember it:

"Precision" start with letter "P", so you can remember it only check prediction. We just look column;

"Recall" start wiht letter "R", so we only look Row. 

Recall: True Positive / (True Positive + False Negative). Out of all the items that are truly positive, how many were correctly classified as positive. Or simply, how many positive items were ‘recalled‘ from the dataset.

Precision: True Positive / (True Positive + False Positive). Out of all the items labeled as positive, how many truly belong to the positive class.

Recall("Hugo Chavez") = 10 / 16

Precision("Hugo Chavez") = 10 / 10

True Positivies / False Positives / False Negatives

Positives: Looks for "Precision - Column"

Negatives: Looks for "Recall - Row"

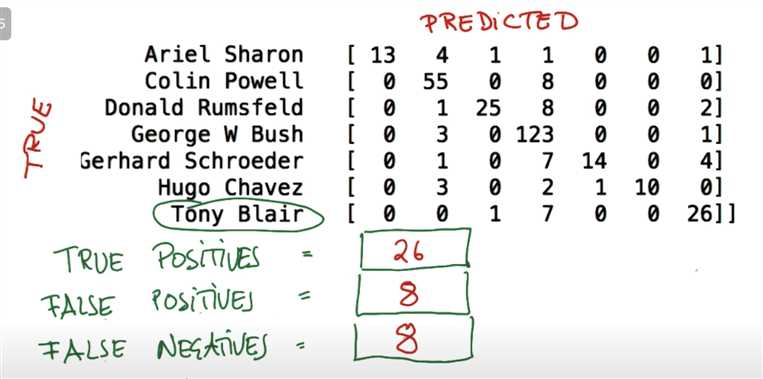
True Positives: 26

False Positives: 1 + 2 + 1 + 4 = 8

False Negatives: 1 + 7 = 8

Exercise:

predictions = [0, 1, 1, 0, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 1, 1, 0, 1, 0, 1]
true labels = [0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 0, 1, 0, 1, 1, 1, 0, 1, 0, 0]

How many true positives are there? (6)

true labels = [0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 0, 1, 0, 1, 1, 1, 0, 1, 0, 0]. 

How many true negatives are there in this example? (9)

predictions = [0, 1, 1, 0, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 1, 1, 0, 1, 0, 1]

How many false positives are there? (3)

predictions = [0, 1, 1, 0, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 1, 1, 0, 1, 0, 1]

How many false negatives are there? (2)

predictions = [0, 1, 1, 0, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 1, 1, 0, 1, 0, 1]

true labels = [0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 0, 1, 0, 1, 1, 1, 0, 1, 0, 0]

What‘s the precision of this classifier? 

precision = TP / TP+FP = 6 / 6+3 = 2/3

What‘s the recall of this classifier?

Recall = TP / TP+FN = 6 / 6+2 = 3/4

My true positive rate is high, which means that when a ___ is present in the test data, I am good at flagging him or her.

[X] POI

[ ] non-POI

My identifier doesn’t have great ____, but it does have good ____. That means that, nearly every time a POI shows up in my test set, I am able to identify him or her. The cost of this is that I sometimes get some false positives, where non-POIs get flagged

[Precision] [Recall]

My identifier doesn’t have great ___, but it does have good ____. That means that whenever a POI gets flagged in my test set, I know with a lot of confidence that it’s very likely to be a real POI and not a false alarm. On the other hand, the price I pay for this is that I sometimes miss real POIs, since I’m effectively reluctant to pull the trigger on edge cases.

[Precision] [Recall]

My identifier has a really great _.

This is the best of both worlds. Both my false positive and false negative rates are _, which means that I can identify POI’s reliably and accurately. If my identifier finds a POI then the person is almost certainly a POI, and if the identifier does not flag someone, then they are almost certainly not a POI.

In statistical analysis of binary classification, the F₁ score (also F-score or F-measure) is a measure of a test‘s accuracy. 

[F1 Score] [low]

[Machine Learning] Evaluation Metrics

原文：https://www.cnblogs.com/Answer1215/p/13435628.html