【并查集】Supermarket POJ - 1456

Supermarket POJ - 1456

题意：

给出\(n\)种商品的价格及最后出售期限（如2表示最晚在第2天出售），每天只能出售一种商品，问最大销售额。

思路：

首先想到贪心。如果商品之间存在时间冲突，显然选择价格更高的那一个更优。

将所有商品按价格从大到小排序。对于第\(i\)个商品，先尝试在它的最后一天卖掉它；若最后一天不能卖，则继续向更前面的日期尝试；如果没有一个日期可以卖，则这个商品就不出售了。

由于价高者优先选择日期，这种策略保证了，若第\(i\)个商品在它的期限\(T_i\)内无法出售，则前\(T_i\)天（含第\(T_i\)天）都已经有价格更高的商品出售。

可以看出，当每个商品查找可出售日期时，都需要一次遍历。那么能不能通过某个商品的最后期限，直接找到在它之前的一个可出售日期呢？

用并查集优化：如果第\(T\)天有商品卖出，则这个日期不可用，将第\(T\)天与未出售商品的第\(T-1\)天合并，则第\(T\)天又是可用的。（显然，按这种合并方法，这里的第\(T-1\)天不一定是一个具体日期，但一定是可用的），

当查询第\(T\)天时，实际上得到的是第\(T\)天之前的一个可用日期。

如此就避免了遍历，而可以直接询问得到一个可出售日期。

如图，第2天出售了商品，将它与前一天合并成一个可用的新集合（因为第1天可用）（浅绿色矩形），根节点就是一个可用日期；随后第4天、第5天都出售了商品，则连同前面最近的可用的第3天一起构成新集合，并且全部指向第3天；第3天出售后，这个集合继续向前合并。

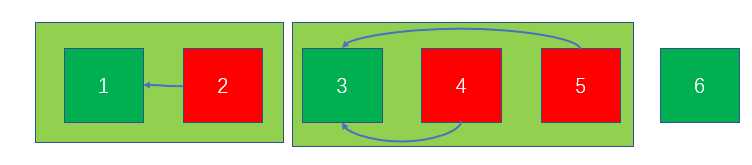
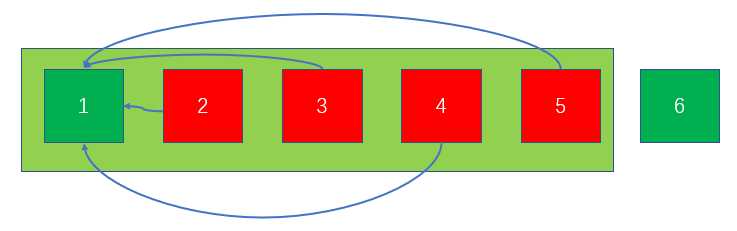
如此，当下一个商品（假设\(T_i=3\)）查询可出售日期时，就会直接得到第1天。

int fa[maxn];

int find(int x) {
    return fa[x] == -1 ? x : fa[x] = find(fa[x]);
}

void merge(int x, int y) {
    x = find(x);
    y = find(y);
    if (x != y) fa[x] = y;
}

struct node {
    int price;
    int ddl;
}goods[maxn];

bool cmp(node x, node y) {
    return x.price > y.price;
}

int main()
{
    //ios::sync_with_stdio(false);
    int n;
    while (cin >> n) {
        int ans = 0;
        memset(fa, -1, sizeof(fa));
        for (int i = 1; i <= n; i++) {
            cin >> goods[i].price >> goods[i].ddl;
        }
        sort(goods + 1, goods + n + 1, cmp);

        for (int i = 1; i <= n; i++) {
            int t = find(goods[i].ddl);
	    //查找在ddl前面的可用日期
            //如果返回-1，也就是ddl指向的根节点是第0天，则说明ddl前的所有日期都不能卖
            if (t > 0) {
                ans += goods[i].price;
              //可以卖掉
                fa[t] = t - 1;
              //暂时先指向前一天
              //在后续的find操作中，会更新为指向t之前的一个可出售日期
            }
        }
        cout << ans << endl;
    }
    return 0;
}

【并查集】Supermarket POJ - 1456

原文：https://www.cnblogs.com/streamazure/p/13460911.html