题目来源:算法竞赛进阶指南
题目标签:数论,快速幂
题目链接:https://www.acwing.com/problem/content/99/
思路:
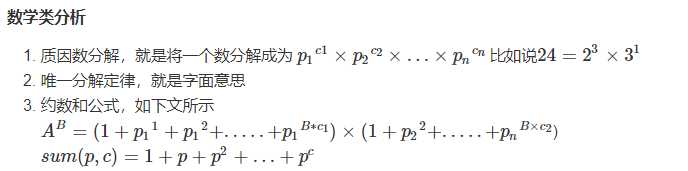
4. 约数个数:(c1 + 1) * (c2 + 1) * (c3 + 1)....
代码:
#include <bits/stdc++.h> using namespace std; const int mod = 9901; int qmi(int a, int k) { a %= mod; int res = 1; while(k) { if(k & 1) res = res * a % mod; a = a * a % mod; k >>= 1; } return res; } //p ^ 0 + ... + p ^ k int sum(int p, int k) { if(k == 0) return 1; if(k % 2 == 0) { //当k是偶数的时候:p * (p ^ 0 + ... + p ^ k - 1) = p ^ 1 + ... + p ^ k return (p % mod * sum(p, k - 1) + 1) % mod; } //当k是奇数的时候 //p ^ 0 + ... + p ^ k = (p ^ 0 + ... + p ^ (k / 2)) + (p ^ (k / 2 + 1) + ... + p ^ k) // = (p ^ 0 + ... + p ^ (k / 2)) + p ^ (k / 2 + 1) * (p ^ 0 + ... + p ^ (k / 2)) 奇数下取整 // = (1 + p ^ (k / 2) + 1) * sum(p, k / 2) return (1 + qmi(p, k/2 + 1)) * sum(p, k / 2) % mod; } int main() { int a, b; cin >> a >> b; int res = 1; //试除法寻找质数因子 for(int i = 2; i <= a; i++) { int s = 0; while(a % i == 0) { s++; a /= i; } if(s) { res = res * sum(i, s * b) % mod; } } if(!a) res = 0; cout << res << endl; return 0; }
原文:https://www.cnblogs.com/realxjr/p/13462281.html