by TimFang|CC-BY-SA 4.0
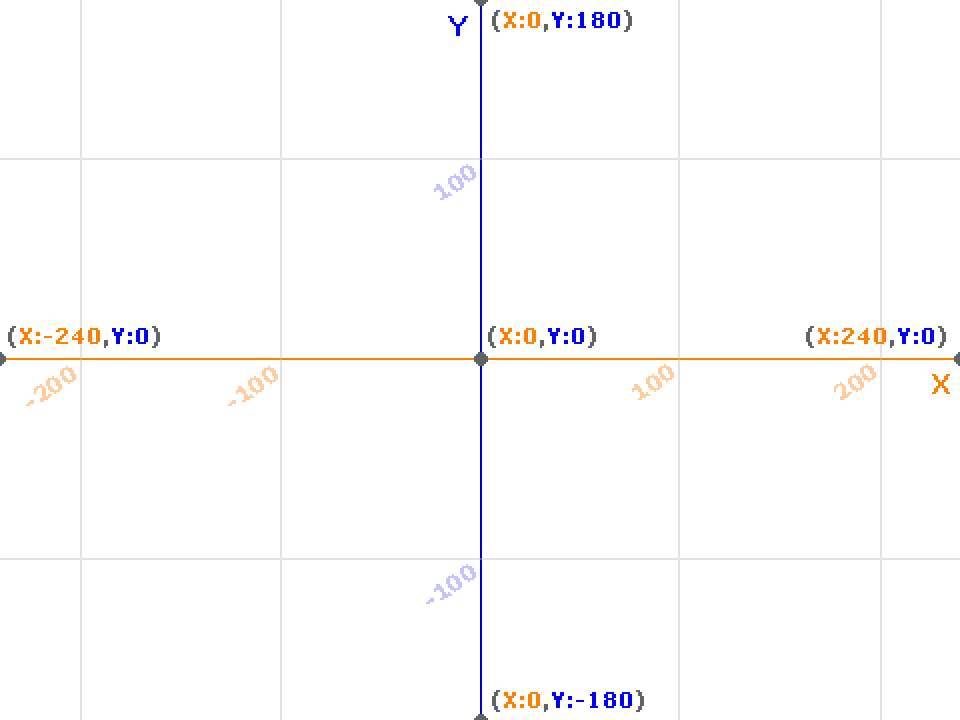
一个物体的x坐标代表它在屏幕左右方向的位置
y坐标代表它在上下方向的位置
Scratch舞台的坐标范围分别是:
x坐标:-240~240
y坐标:-180~180
3D坐标系增加了一个z轴
其实就是2D坐标在纵深方向的扩展
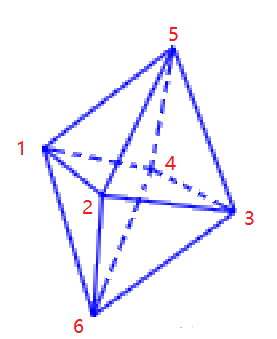
比如下面这个八面体,它有6个顶点
上半部分和下半部分分别有四个三角形
它是最简单的可以一笔画出来的多面体
比如依次连接点1-6-2-5-3-6-4-5-1-2-3-4-1就可以不重复任一条边把它画出来
简单来说,只要我们知道了八面体的6个顶点的3D坐标,我们就能一笔过把它画出来
scratch舞台是2d的
我们通过屏幕看到的3D物体
实际上是它根据透视原理在屏幕上的一个2D投射
在scratch的舞台上
z轴越大 图案的大小越小
即:近大远小
一个3D物体的大小和形状,与:
物体位置
摄像机位置
屏幕位置
有关.
那么在3D内的某点在2D中坐标该如何计算?
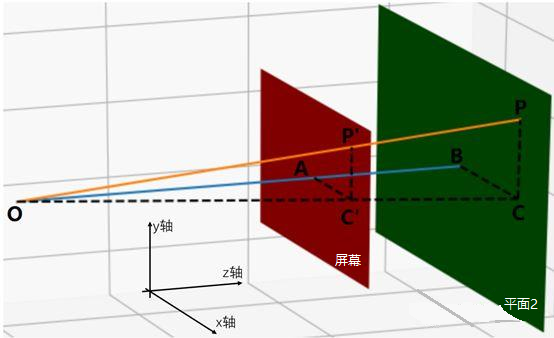
P代表3D空间中1点
坐标为x,y,z
O为摄像机位置
要求P在屏幕上投射点P‘的位置 该如何求?
强调,3D点的投射除了和它本身的坐标有关之外,还和视点位置、投射屏幕位置有关。这三个因素是互相影响的。忽略了任何一个因素都不能得出投射点坐标!
绿色平面代表P经过的,和红色屏幕平面平行的一个平面
线段OAB和红色以及绿色平面都垂直
我们为了方便计算,让红色平面与x轴和y轴组成的平面平行.
这样,
线段OA,OB和z轴平行(并垂直于红色及绿色平面);
线段BC以及AC’与x轴平行线段PC;
P’C’与y轴平行;
因为BC与AC’平行、PC与P’C’平行,根据相似三角形的特点,我们很容易知道:
OA/OB=AC’/BC=P’C’/ PC
所以,如果知道:
P点坐标x,y,z
O点坐标ox,oy,oz
红色平面的z坐标值pz
则:
OA=pz–oz
OB=z–oz
BC=x–ox
PC=y–oy
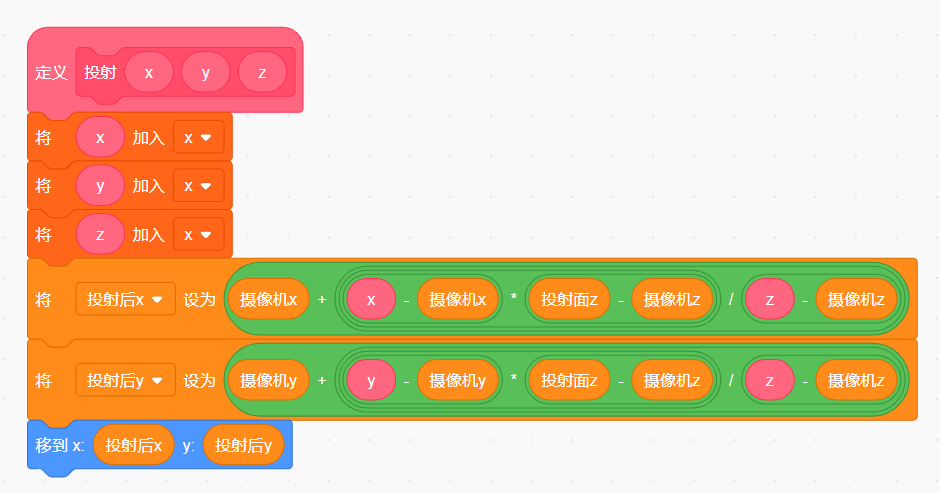
则P在红色屏幕平面投射点P’的x、y轴坐标值
P’的x坐标 =
ox+ AC’=
ox+[(pz–oz)*(x-ox)/(z-oz)]
P’的y坐标 =
oy+P’C’=
oy+[(pz-oz)*(y-oy)/(z-oz)]
接下来我们就用这个结论在scratch里画出一个3D的八面体来
Scratch的2D舞台就是上面图中的红色屏幕,我们要做的就是把3D物体在2D屏幕上的投射画出来.所以在画之前我们先要在自己心中有一个3D坐标,摄像机位置,屏幕的位置,物体的位置.
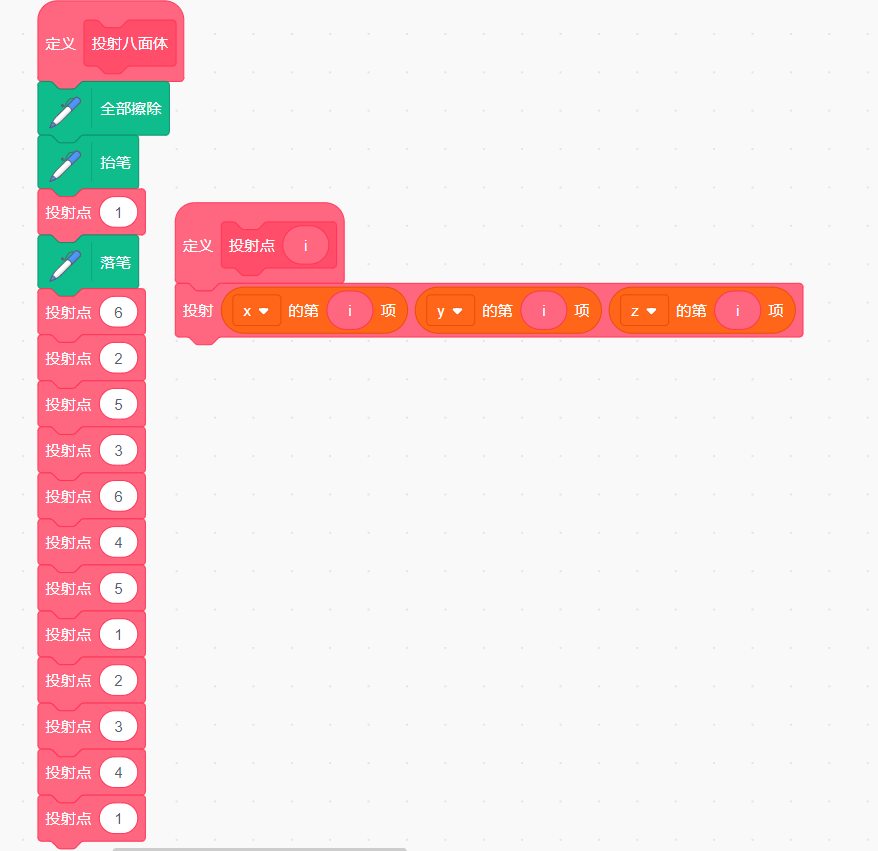
八面体有6个顶点,如下图依次连接点1-6-2-5-3-6-4-5-1-2-3-4-1就可以一笔过画出它来:

首先我们用三个数组分别保存八面体6个顶点的x,y,z坐标
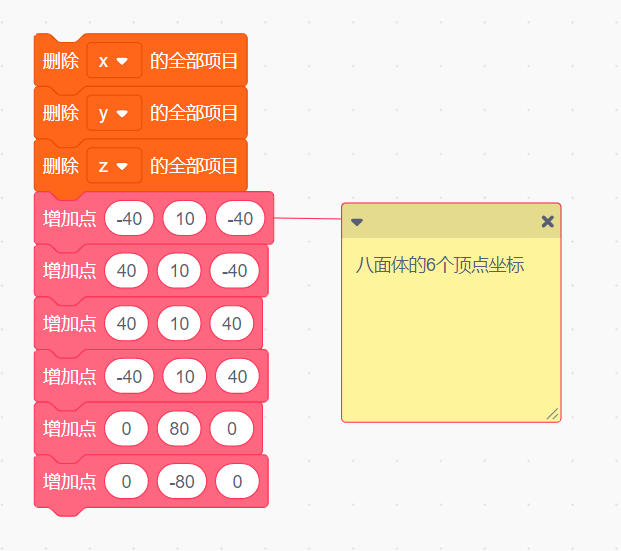

定义摄像机及投射屏幕平面的位置(为了方便计算,我们让投射平面与x轴和y轴组成的平面平行,所以投射面只有一个z值)

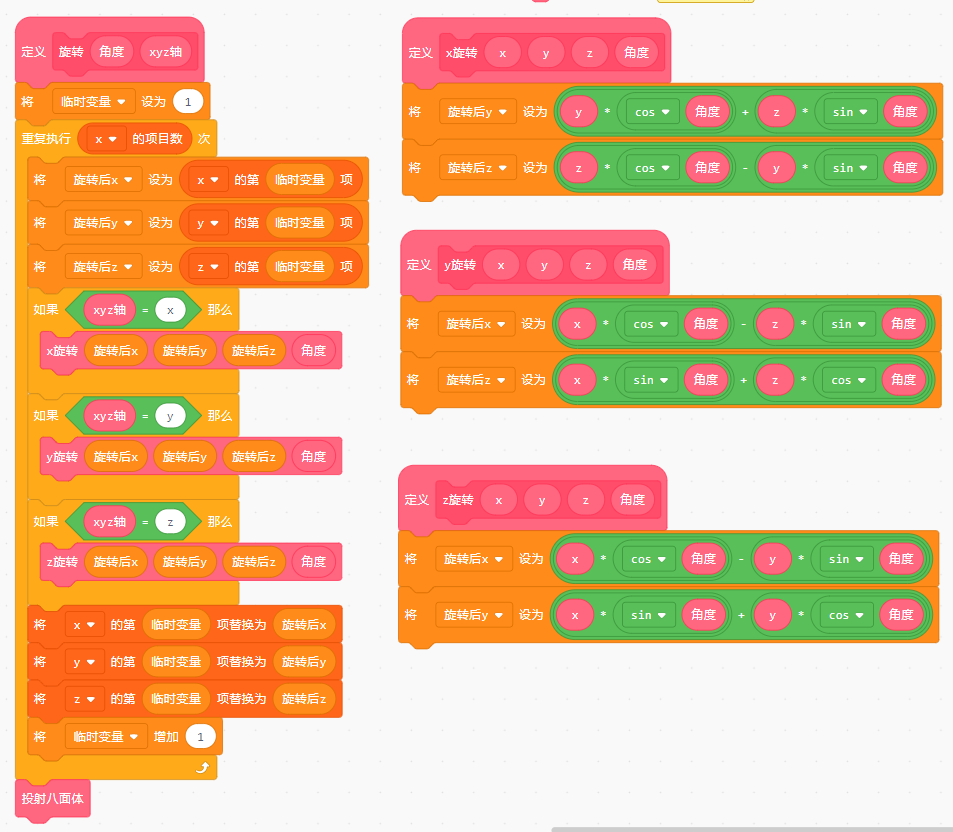
根据前面3D到2D屏幕的投射公式,自定义一个积木用来投射转换
接下来就依次投射1-6-2-5-3-6-4-5-1-2-3-4-1点,用画笔画出连接各点的轨迹
物体移动只需要改变它所有顶点的x,y,z值,然后再重新投射一次就可以了。实现程序如下
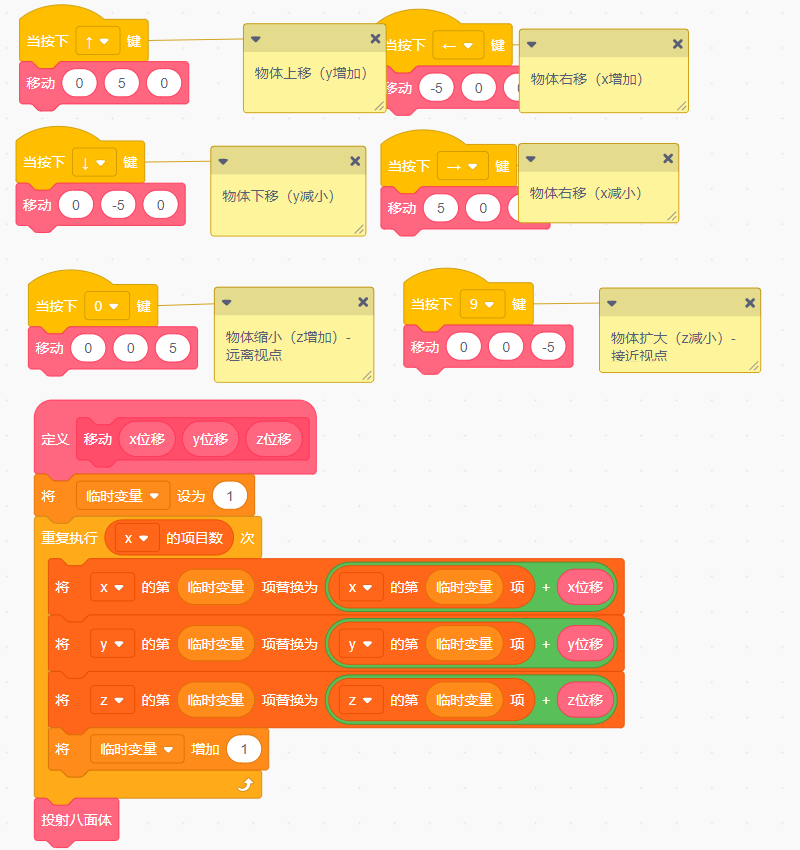
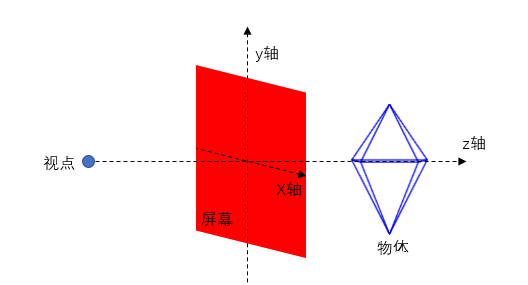
注意这里物体的移动是在原3D空间的移动,所以物体在x轴方向或y轴方向移动后,在屏幕上的投射会产生一定的旋转效果。观察位置离投射平面越近,这种旋转效果越明显。
物体在z轴方向的移动会产生物体大小变化的视觉效果:物体远离视点时物体投射缩小,接近视点时物体投射增大。原理如下图所示
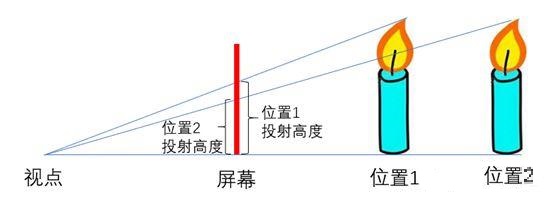
移动的效果如下:

物体旋转涉及到三角函数的知识。推导过程需要一定的篇幅。我们只需要记住简单的结论来应用就可以了。
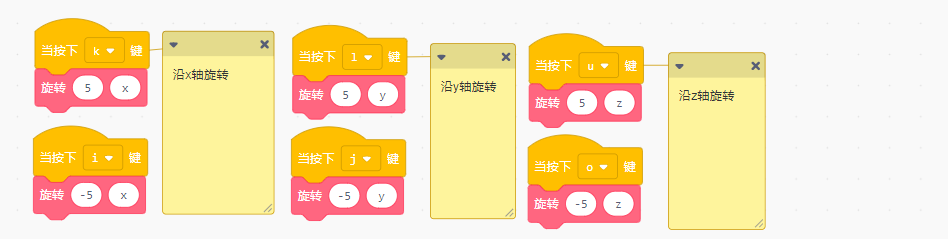
旋转可以分为三种:沿x轴的旋转、沿y轴的旋转和沿z轴的旋转。
沿x轴旋转时,物体的x坐标不变,y坐标和z坐标的变换规律是(A为旋转角度):
新的y坐标=ycosA+zsinA
新的z坐标=zcosA–ysinA
沿y轴旋转时,物体的y坐标不变,x坐标和z坐标的变换规律是(A为旋转角度):
新的x坐标=xcosA–zsinA
新的z坐标=xsinA+zsinA
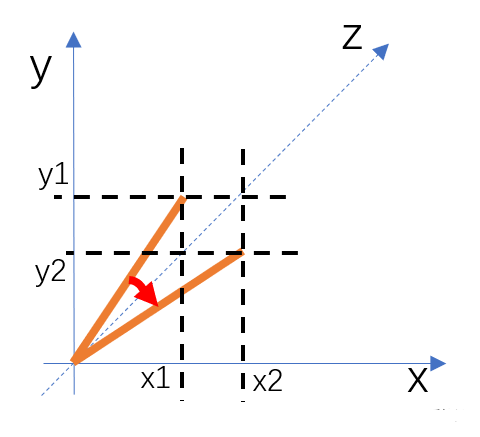
沿z轴旋转时,物体的z坐标不变,x坐标和y坐标的变换规律是(A为旋转角度):
新的x坐标=xcosA–ysinA
新的y坐标=xsinA+ycosA
下图显示了沿z轴旋转时的变换情况。有兴趣的同学可以自己推导出坐标的变换规律。
注意上面说的坐标变化都是物体原3D坐标的变化,而不是投射在2D平面上的投射坐标的变化。换言之,旋转改变物体坐标后,还要重新计算投射坐标。
旋转的实现方法:
效果如下

程序地址 https://aerfaying.com/Projects/518702/Editor
原文:https://www.cnblogs.com/TimFang/p/13496714.html