匈牙利算法

1 先看一些基础概念：

最大匹配：

给定一个二分图G，在G的一个子图M中，M的边集中的任意两条边都不依附于同一个顶点，则称M是一个匹配。选择这样的边数最大的子集称为图的最大匹配问题，如果一个匹配中，图中的每个顶点都和图中某条边相关联，则称此匹配为完全匹配，也称作完备匹配。

增广路（增广轨）：

若P是图G中一条连通两个未匹配顶点的路径，并且属于M的边和不属于M的边(即已匹配和待匹配的边)在P上交替出现，则称P为相对于M的一条增广路径（举例来说，有A、B集合，增广路由A中一个点通向B中一个点，再由B中这个点通向A中一个点……交替进行）。

匈牙利算法虽然根本上是最大流算法，但是它不需要建网络模型，所以图中不再需要源点和汇点，仅仅是一个二分图。每条边也不需要有方向。

图1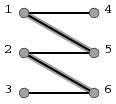图2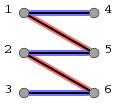
图1是给出的二分图中的一个匹配：［1，5］和［2，6］。图2就是在这个匹配的基础上找到的一条增广路径：3->6->2->5->1->4。

2 回到匈牙利算法：

匈牙利算法是由匈牙利数学家Edmonds于1965年提出，因而得名。匈牙利算法是基于Hall定理中充分性证明的思想，它是部图匹配最常见的算法，该算法的核心就是寻找增广路径，它是一种用增广路径求二分图最大匹配的算法。

白话描述具体参考https://blog.csdn.net/dark_scope/article/details/8880547

算法实现参考https://www.cnblogs.com/walter-xh/p/10698834.html

#include <iostream>
#include <array>

using namespace std;

bool line[4][4] = {{true, true, false, false}, {false, true, true, false}, {true, true, false,false}, {false, false, true, false}};
array<bool, 4> used = {false, false, false, false};
array<int, 4> girl = {-1, -1, -1, -1};

bool find(int x){
    for(int i = 0; i < 4; ++i){
        if(line[x][i] == true && used[i] == false){
            used[i] = true;
            if(girl[i] == -1 || find(girl[i])){
                girl[i] = x;
                return true;
            }
        }
    }
    return false;
}

int main(){
    for(int i = 0; i < 4; ++i){
        used.fill(false);
        find(i);
    }
    for(int i = 0; i < 4; ++i){
        cout << "girl: " << i << " <----> " << girl[i] << endl;
    }
    return 0;
}

匈牙利算法

原文：https://www.cnblogs.com/waynew/p/13512092.html