模板题: CF600E Lomsat gelral

题目描述

一棵树有n个结点，每个结点都是一种颜色，每个颜色有一个编号，求树中每个子树的最多的颜色编号的和。

一些定义

• 启发式算法:启发式算法是指基于经验和直观感觉，从而对一些算法的优化。

举例:并查集的按秩合并

在并查集的按秩合并中,我们将小的集合往大的集合上合并,这样明显有利于加快并查集的祖先查找

算法流程

• 首先是一次\(bfs\),求出每个节点的重儿子

void dfs1(int u,int fa){
	size[u] = 1 ;//子树大小
	for(int i = head[u];i;i = edge[i].next){
		int v = edge[i].to;
		if(v==fa) continue;
		dfs1(v,u);
		size[u]+=size[v];
		if(size[v]>size[son[u]]) son[u] = v;//找重儿子
	}
	
}

接下来定义两个数组\(cnt[]\)和\(c[]\),分别代表存放的某颜色在“当前”子树中的数量和存放某节点的颜色

这里的"当前"指的就是目前正在处理的节点(如果给每个节点都开一个\(cnt\)的话则会\(MLE\))

• 如果目前正在处理的节点是轻儿子,就把它的答案计入并删除其贡献

• 反之,如果是重儿子,也把它的答案计入,但不删除其贡献

void cunt(int u,int fa,int val){
	c[color[u]]+=val;//val为1代表计入贡献,为-1代表删除贡献
	if(c[color[u]] > maxn){//最多的颜色
		maxn = c[color[u]];
		sum = color[u];
	}
	else if(c[color[u]] == maxn){
		sum+=color[u];
	}
	for(int i=head[u];i;i=edge[i].next){
		int v = edge[i].to;
		if(v==maxson||v==fa) continue;//如果是u的重儿子,直接跳过
		cunt(v,u,val);//dfs暴力计贡献
	}
}
void dfs2(int u,int fa,int keep){//keep代表是否保留该贡献
	for(int i=head[u];i;i=edge[i].next){
		int v = edge[i].to;
		if(v==son[u]||v==fa) continue;//是重儿子直接跳过
		dfs2(v,u,0);
	}
    
	if(son[u]){//如果有重儿子
		
		dfs2(son[u],u,1);//keep为1,保留其贡献
		maxson = son[u];//记u节点的重儿子
	}
	cunt(u,fa,1);//暴力统计其非子树贡献
	maxson = 0;
	ans[u] = sum;//记录答案
	if(!keep){//如果不是重儿子,则将其贡献删除
		cunt(u,fa,-1); 
		sum = maxn = 0 ;
	}
}

整个\(dfs\)大致可以分为下面四个流程:

• 记录轻儿子及其子树的答案且删除其贡献

• 记录重儿子及其子树的答案且不删除其贡献

• 暴力统计\(u\)及其所有轻儿子的贡献合并到刚算出的重儿子信息里

• 删除该删除的贡献

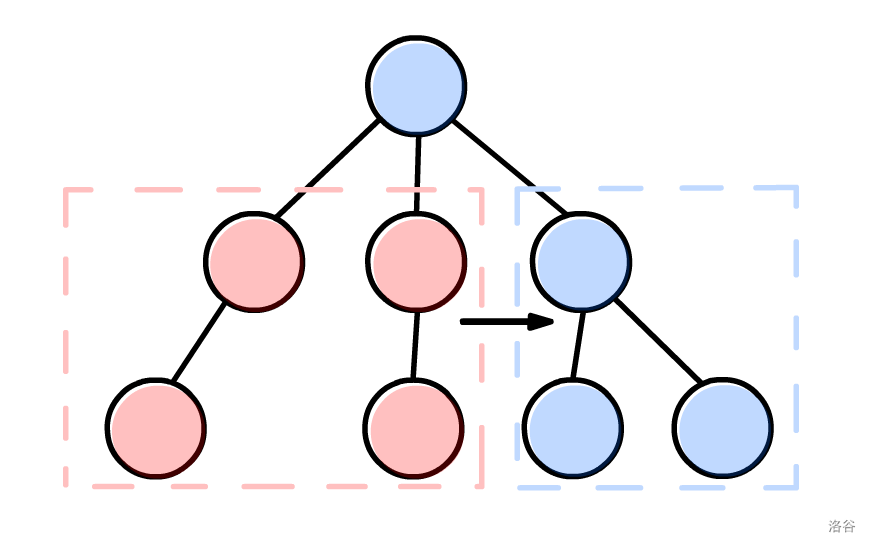
这样一轮下来相当于是遍历了两遍轻儿子,一遍重儿子,显然效率是较高的

时间复杂度为\(O(nlogn)\),具体怎么证还不太清楚

\(code:\)

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int MAXN = 100010;
struct e{
	int next,to;
}edge[MAXN<<1];
int size[MAXN],son[MAXN];
int color[MAXN],c[MAXN];
int maxn , sum;
int head[MAXN<<1],n,cnt = 0;
int ans[MAXN] , maxson;
void add(int u,int v){
      cnt++;
      edge[cnt].to = v;
      edge[cnt].next=head[u];
      head[u]=cnt;
      return;
}
void dfs1(int u,int fa){
	size[u] = 1 ;
	for(int i = head[u];i;i = edge[i].next){
		int v = edge[i].to;
		if(v==fa) continue;
		dfs1(v,u);
		size[u]+=size[v];
		if(size[v]>size[son[u]]) son[u] = v;
	}
	
}
void cunt(int u,int fa,int val){
	c[color[u]]+=val;
	if(c[color[u]] > maxn){
		maxn = c[color[u]];
		sum = color[u];
	}
	else if(c[color[u]] == maxn){
		sum+=color[u];
	}
	for(int i=head[u];i;i=edge[i].next){
		int v = edge[i].to;
		if(v==maxson||v==fa) continue;
		cunt(v,u,val);
	}
}
void dfs2(int u,int fa,int keep){
	for(int i=head[u];i;i=edge[i].next){
		int v = edge[i].to;
		if(v==son[u]||v==fa) continue;
		dfs2(v,u,0);
	}
	if(son[u]){
		
		dfs2(son[u],u,1);
		maxson = son[u];
	}
	cunt(u,fa,1);
	maxson = 0;
	ans[u] = sum;
	if(!keep){
		cunt(u,fa,-1); 
		sum = maxn = 0 ;
	}
}
signed main(){
	scanf("%lld",&n);
	for(int i=1;i<=n;i++){
		scanf("%lld",&color[i]);
	}
	for(int i=1;i<n;i++){
		int u,v;
		scanf("%lld%lld",&u,&v);
		add(u,v);
		add(v,u);
	}
	dfs1(1,0);
	dfs2(1,0,0);
	for(int i=1;i<=n;i++){
		cout<<ans[i]<<" ";
	}
	return 0;
} 

最近沉迷stg无法自拔了

树上启发式合并

原文：https://www.cnblogs.com/xcxc82/p/13513450.html