在这篇博文中,我希望能从数学的角度帮助你理解计算机中的补码世界,并尝试解释以下问题:
符号位为什么是最高位,为什么1 表示负,0 表示正?0 表示正,1 表示负,为啥不是 0 表示负,1 表示正?
为什么补码 1000 0000 表示 -128 ?
为什么补码能够实现减法运算?
关于原码、反码、补码的计算这里就不赘述了,但是如果你对于原码、反码、补码的计算还是通过一个数 -> 二进制原码 -> 正数不变,负数保持符号位,其他位取反 得反码 -> 反码+1得补码
另外也有上面的3个疑问的话
我强烈建议你忘掉之前关于原码、反码和补码的认知
我首先抛出三个问题,希望你带着这三个问题去阅读,当你能给出这两个问题的答案的时候,上面的3个问题也有答案了
在一个环形系统中,能表示的数是有限的。例如在下面的表盘中,你能表示的数只有0~11,大于等于12的数,会被舍弃一部分,再在表盘上表示出来。
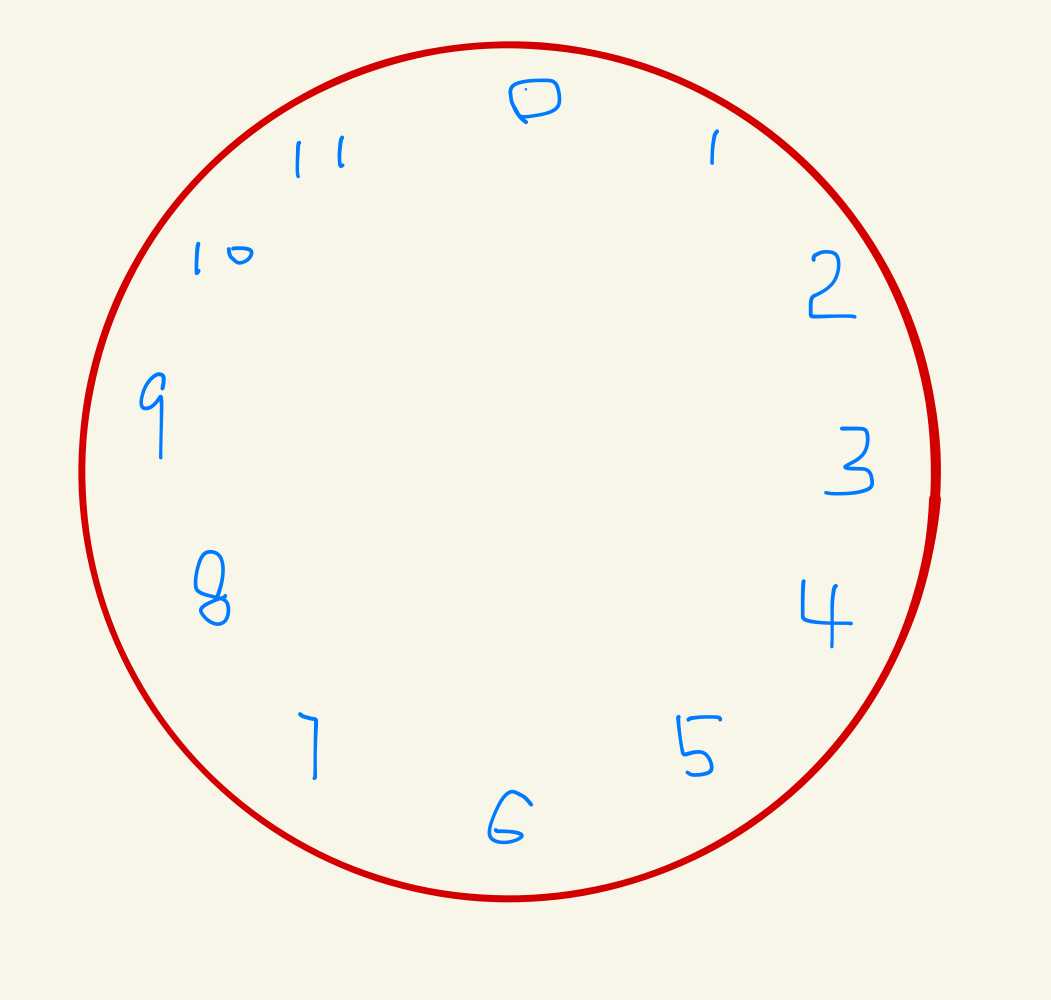
比如15点,在钟表上表现的是3。当表针越过11的时候,又从0开始,直到3。如果在钟表的世界里,要表示27呢?钟表上无法表示准确的数字,27在这里只能被表示为3。准确地说,在超出这个系统极限值的时候,这个系统只能用「余数」来计量
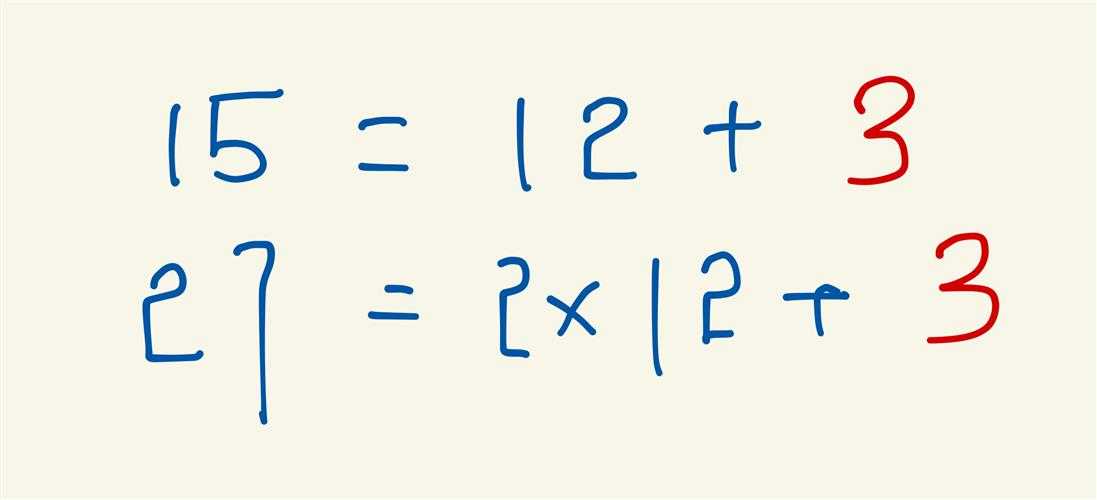
在这里,所有被12除,余数为3的数,都被归为1类。在这里,还有余数为0、1、2...11的类
而15和27,称为 15和27关于模12同余,它们的余数就是3
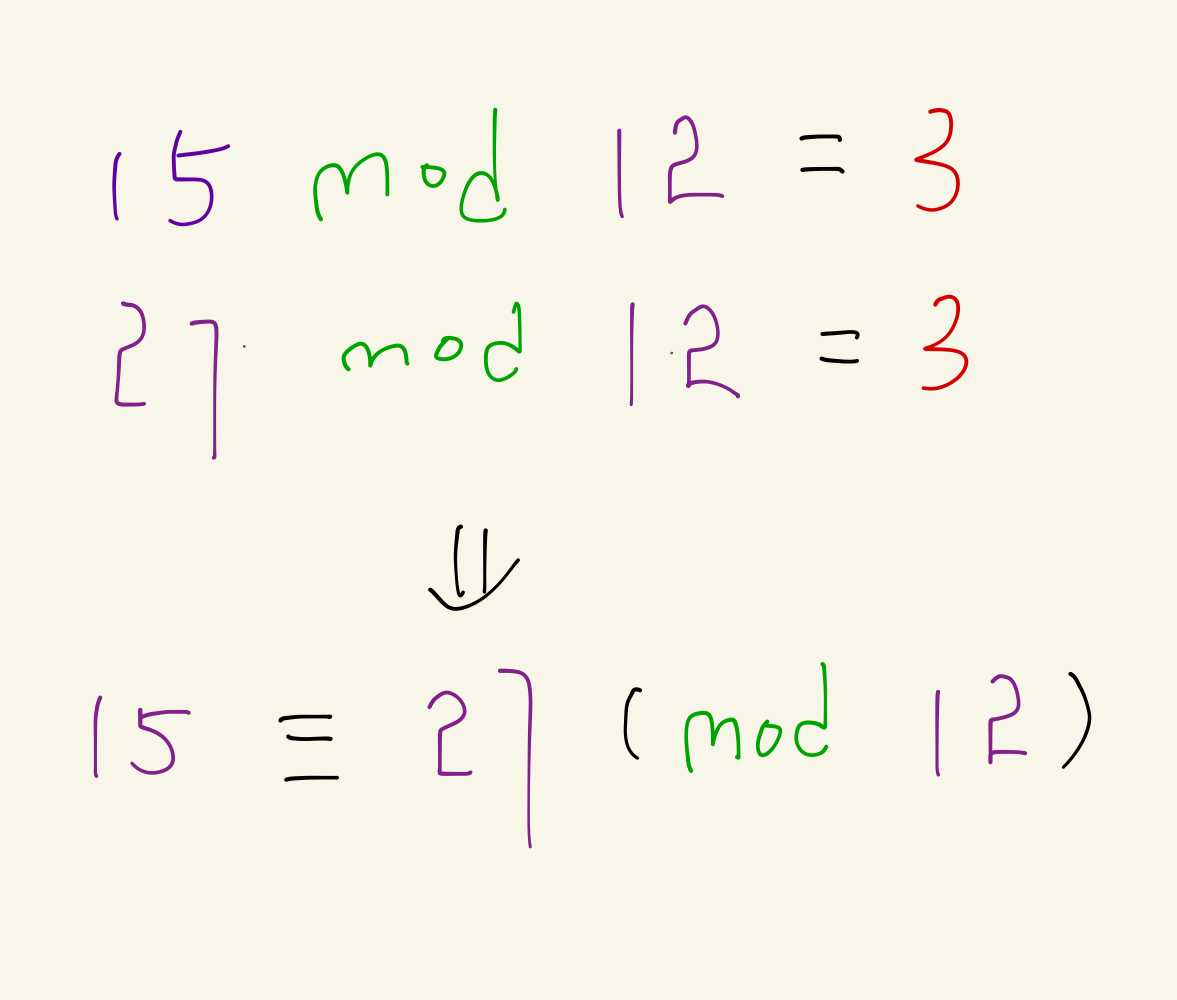
在这个系统中,能表示的数只有「余数」,表盘上的数字都是被12除后的余数
我们可以这样理解这个系统:这个系统将整数分成了12类——被12除余0、1、2、3、4、5、6、7、8、9、10、11的类
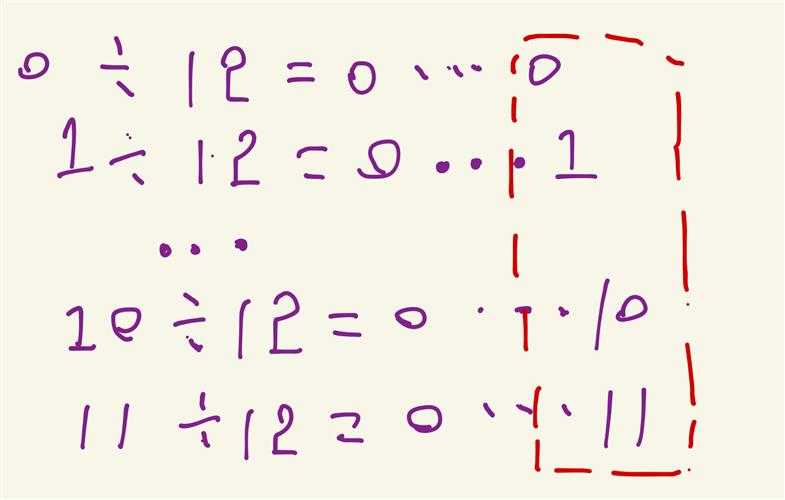
我们来看看「什么是奇数?什么是偶数?」
偶数是被2除余0的整数,奇数是被2除余1的整数。
通过模2我们将整数分成了两类:余0和余1的数,也就是偶数和奇数
回到我们的表盘,通过模12,所有的整数也能被分成12类,分别是余0、1、2、3、4、5、6、7、8、9、10、11的类
所有的整数对模12做取模运算,按照它们的余数我们可以给它们分类。
1、13、-11、-23是同一类!
到这里,我们可以给出第一个问题的答案了。关于同余是这样定义的:如果两个数a、b除以模m,余数一样,就称整两个数关于模m同余,记为
同余的意义就是分类!
很容易理解计算机实际上就是一个环形系统。我们以4位bit来看看
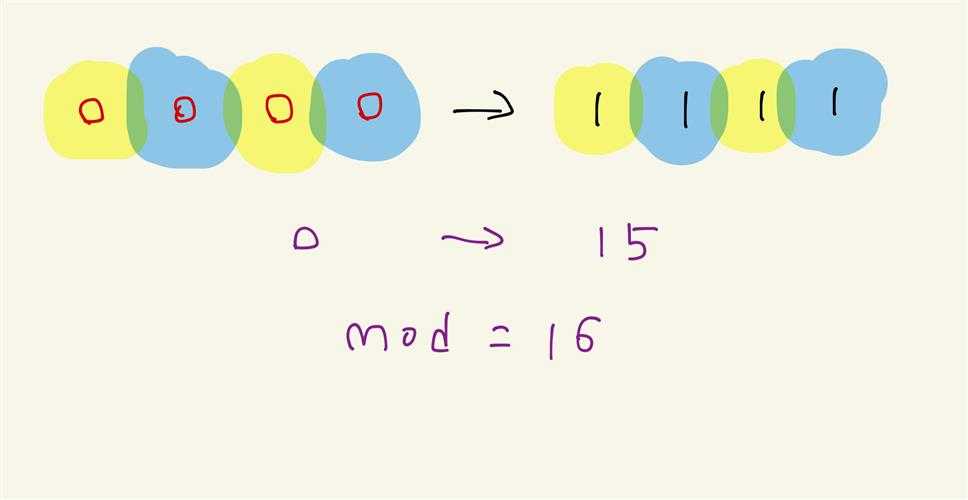
在这个系统中,我们怎么表示负数呢?比如说 -2 ?既然这是一个环形系统,结合同余来看这个世界会变得极其容易。
根据同余,-2 在这里和14 是同一类!所以我们可以用 14 的机器码来表示 -2
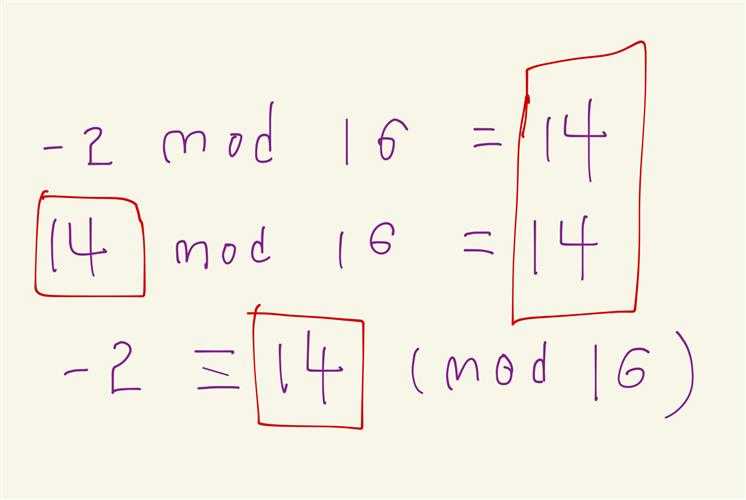
14 的机器码是 1110
现在问题出现了,1110 原来就是表示正数的14的,现在又要表示-2。那么当机器给我们这个二进制的时候,我们到底是把它看做14还是-2呢?
我们有一种做法:就是把0~15个数分成了两组,0~7的机器码还是代表原来的0~7,8~15的机器码表示了-8~-1
当我们采用了上述这种分法的时候,欢迎来到补码的世界。这正是我们现在的计算机世界——补码世界
我们分别算一下-8~-1的关于模16的同余数以及同余数的二进制机器码

这些表示是不是很熟悉?最高位的 1 表示负号,补码 1111 转反码 1110 转原码 1001 = -1。符号位 1 表示负数,0 表示正数,不是拍脑袋决定的,而是基于同余的思想
说到底,补码的世界就是同余的世界啊!!!
到这里,我们可以解释负数在4位系统中的表示了。通过引入了同余,将这个世界中一半的大数转为了小数对应的负数
通过引入同余/补码,我们可以表示负数,可以只用加法器实现减法运算

在这个补码/同余的世界里,原生支持减法运算!!!
很容易得到,在8位系统中,mod = 1 0000 0000 = 256,负数的范围是-128 ~ -1,正数是0 ~ 127
来看两个例子:
「例子1」: 30 - 70 = ?
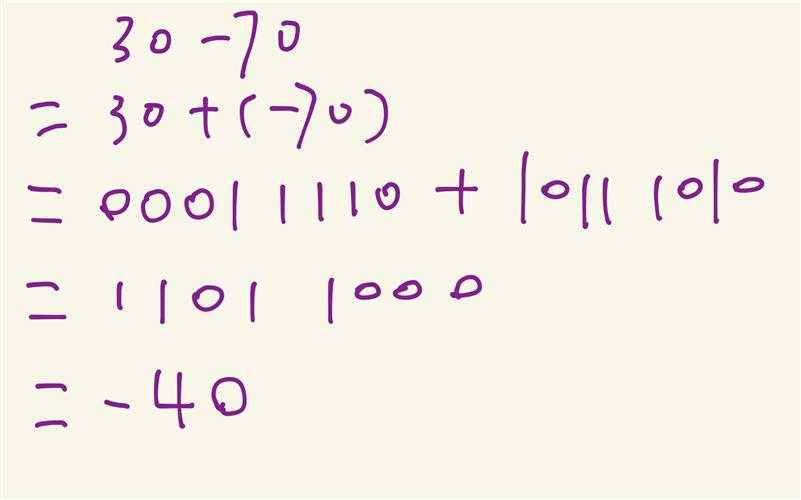
记住这是一个补码的世界,我们没必要管原码和反码,让它们见鬼去吧!!!
30 的补码是0001 1110,这个很顺利,我们直接转二进制就行了,因为 30 三 30 (mod 256)
-70 有点波折,因为我们需要知道它占用了哪个同余数的机器码,256 - |-70| = 186。它占用了186 的机器码,也就是 1011 1010
两个机器码直接相加得到 1101 1000。这是补码!!直接转是216。但是这个值大于127,我们知道这个数的机器码被它的同余数-40 占用了
因为256 - |-40| = 216
「例子2」: 100 - 50 = ?
在这里,我们尝试进入补码世界,但是不用二进制表示,为了符合我们直观
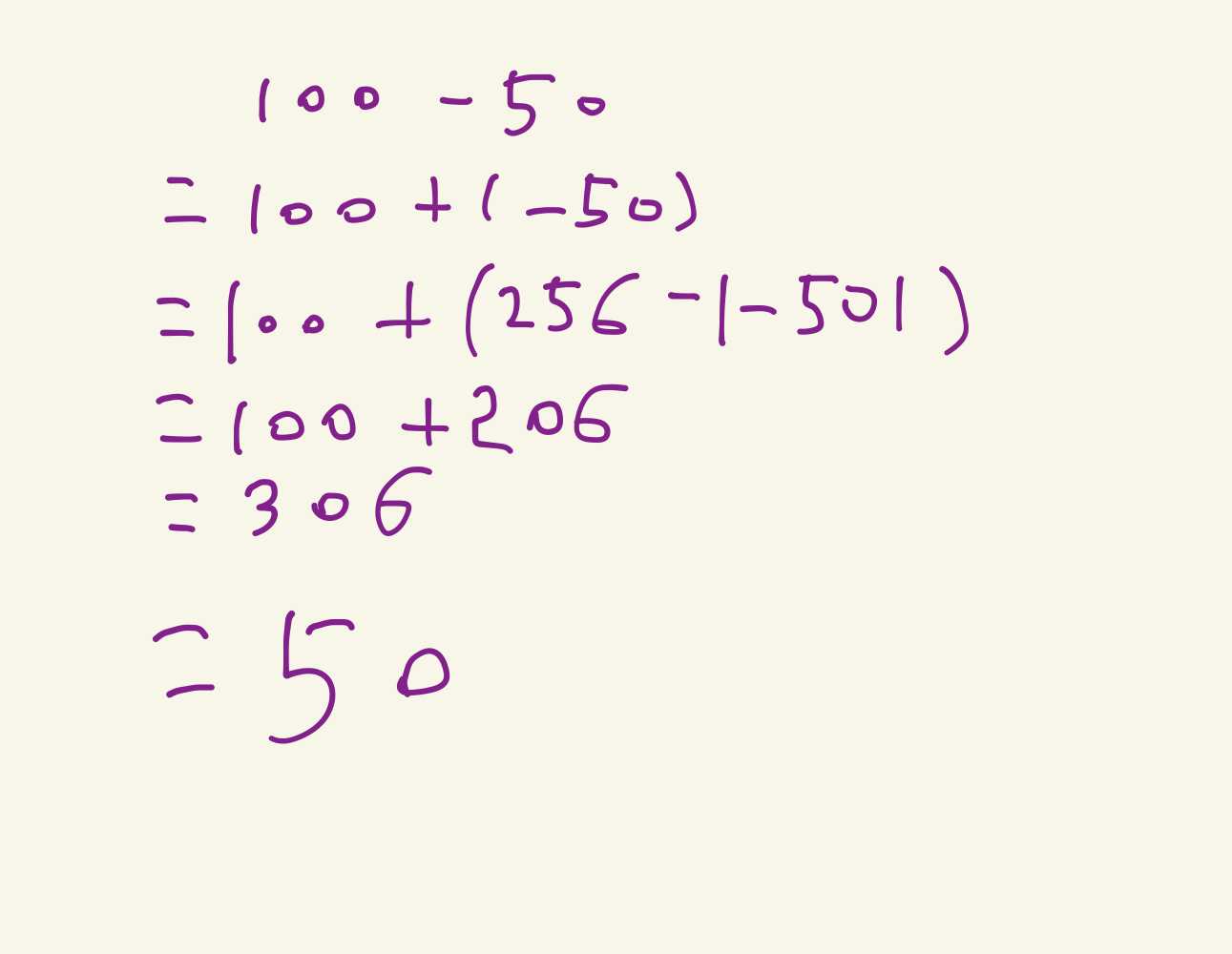
记住这是一个环形世界,306 在这个世界和 50 是一类。 306 三 50 (mod 256),50 的机器码并没有被占用,所以最终的答案就是 50
总结一下上面两个例子,在8位系统中,模是256。能表示的数是 -128 ~ 127。超出这个范围的数都会根据同余被归到其中的一类
为了说明补码原生支持减法。我们想象一个8位系统,我们希望它能表示的数的范围是 -100 ~ 155
现在计算 50 - 30 和 30 - 50
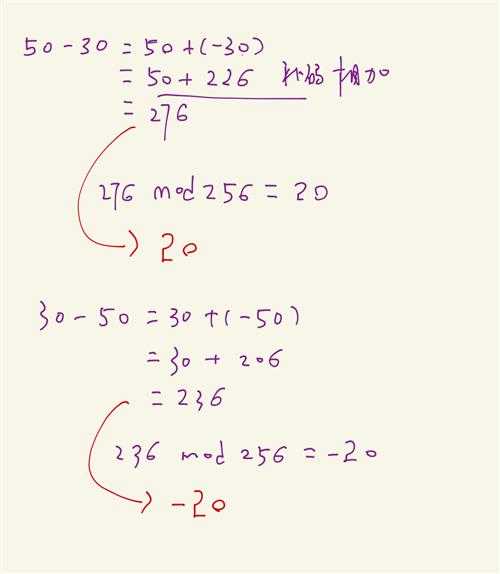
看到了吗?在这个补码的世界里,才不管你是怎么分的,分成-128 ~ 127 也好,分成 -100 ~ 155 也罢,老子天然支持减法运算
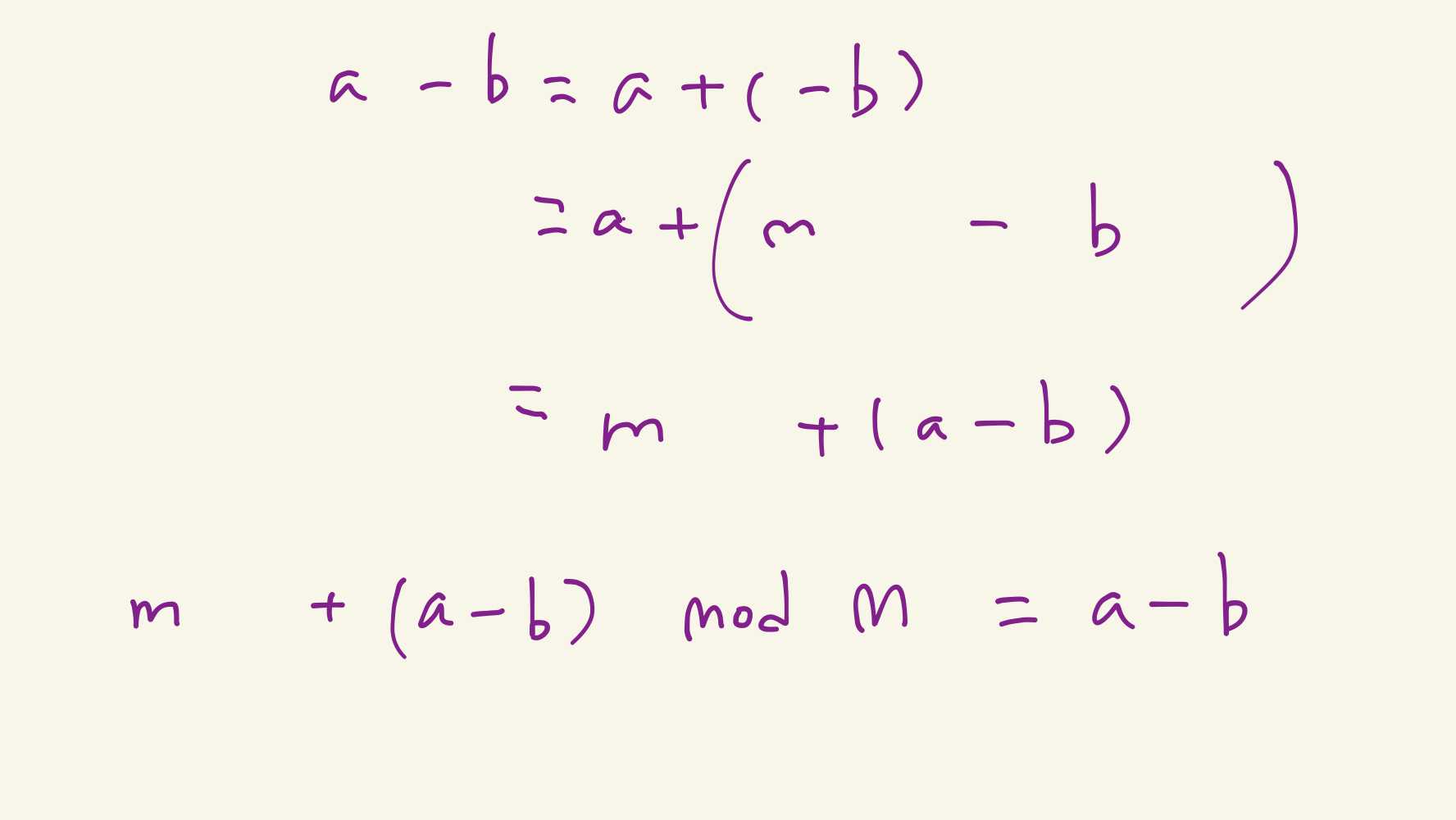
为了帮助你融会贯通补码这门武功,我决定带着你闯荡一遍8位系统的江湖。在这里,不用管1 和 0,二进制也好,16进制也好,思想都是一样的。
我们再来计算 109 - 9 和 9 - 109,记住,不要用 1 和 0 的机器码,我们纯用补码的思想(也就是同余)来搞事
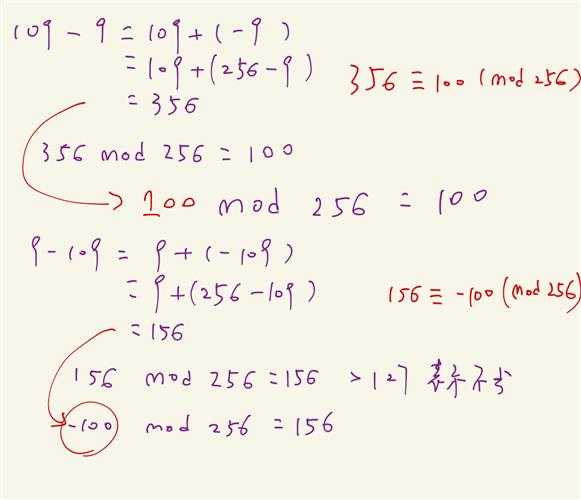
到了这里,是不是觉得补码也就那么回事了。
现在,你是不是可以自己解决开篇的三个疑问了呢?带着同余的思想去干掉这三个疑问吧!!
原文:https://www.cnblogs.com/zongwu/p/13516639.html