恒定外部电流

求解原函数

单位及初始条件说明

1. v的单位为mV
2. t对应的单位为ms
3. I对应的单位为namp
4. 其中 \(v_{0}\) 是某一段函数的初始膜电位，对应为初始时刻 \(t_0\)，是某一段方程的初始条件

1.静息时刻

Condition

1. \(v_0=-70\text{mV}\quad\text{for}\quad t_0=0\)
2. \(I=0\)

Solution

2.外部恒定刺激

Condition

1. \(v_0=-70\text{mV}\quad\text{for}\quad t_0=5\text{ms}\)

2. \(I=10\text{namp}\)

Solution

3.外部刺激消失，缓慢恢复到静息电位

Condition

1. \(v_0\approx30\text{mV}\quad\text{for}\quad t_0=80\text{ms}\)
2. \(I=0\)

Solution

代码

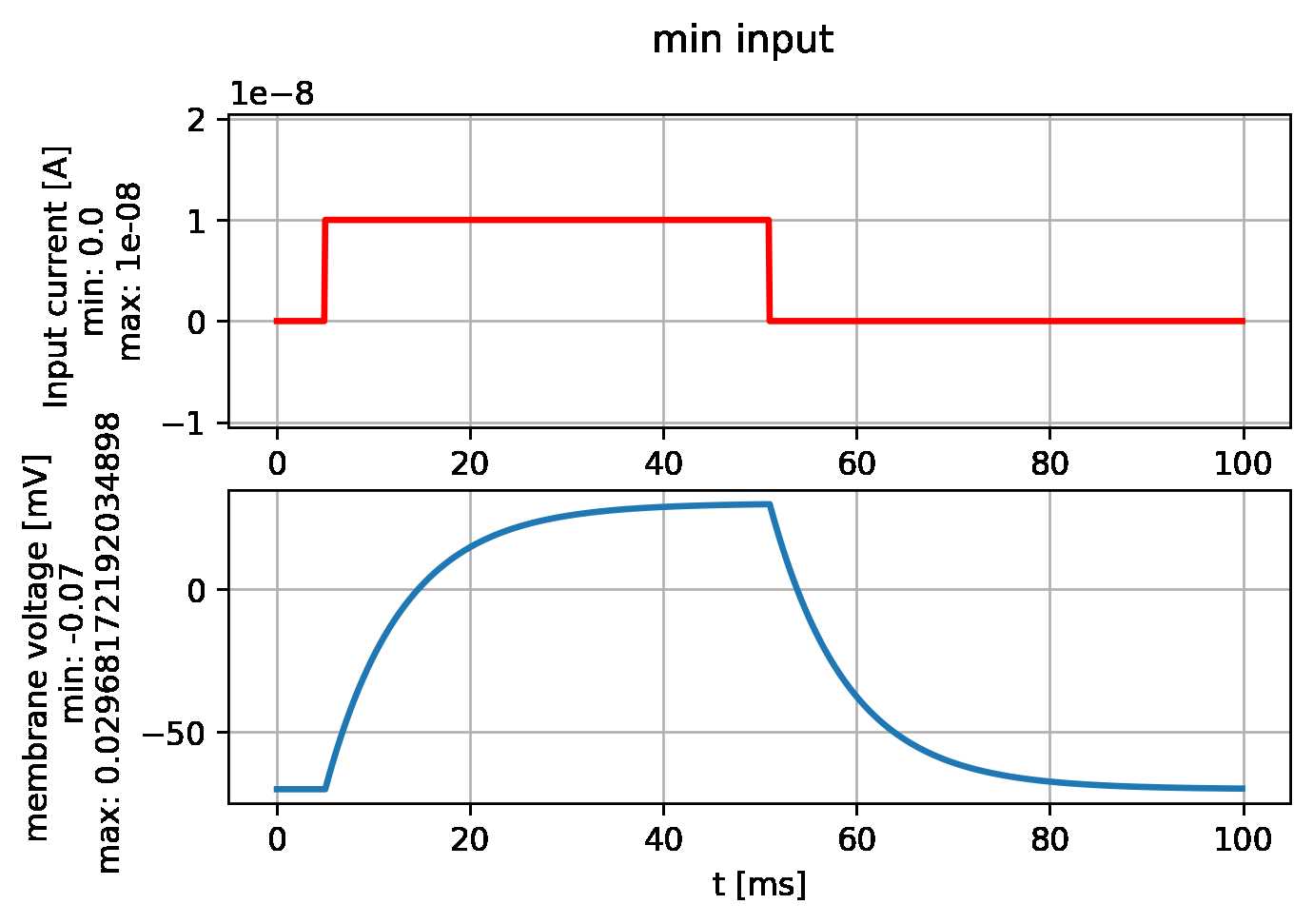
I_min = 10 * namp

# create a step current with amplitude = I_min
input_current = input_factory.get_step_current(
    t_start=5, t_end=50, unit_time=b2.ms,
    amplitude=I_min)  # set I_min to your value


# differential equation of Leaky Integrate-and-Fire model
eqs = """
dv/dt = ( -(v-v_rest) + membrane_resistance * input_current(t,i) ) / membrane_time_scale : volt (unless refractory)"""

# LIF neuron using Brian2 library
neuron = b2.NeuronGroup(
    1, model=eqs, reset="v=v_reset", method="linear")
neuron.v = v_rest  # set initial value

结果

Reference

LIF模型

LIF模型

原文：https://www.cnblogs.com/ctrlplayer/p/13519501.html