题解——最大的和

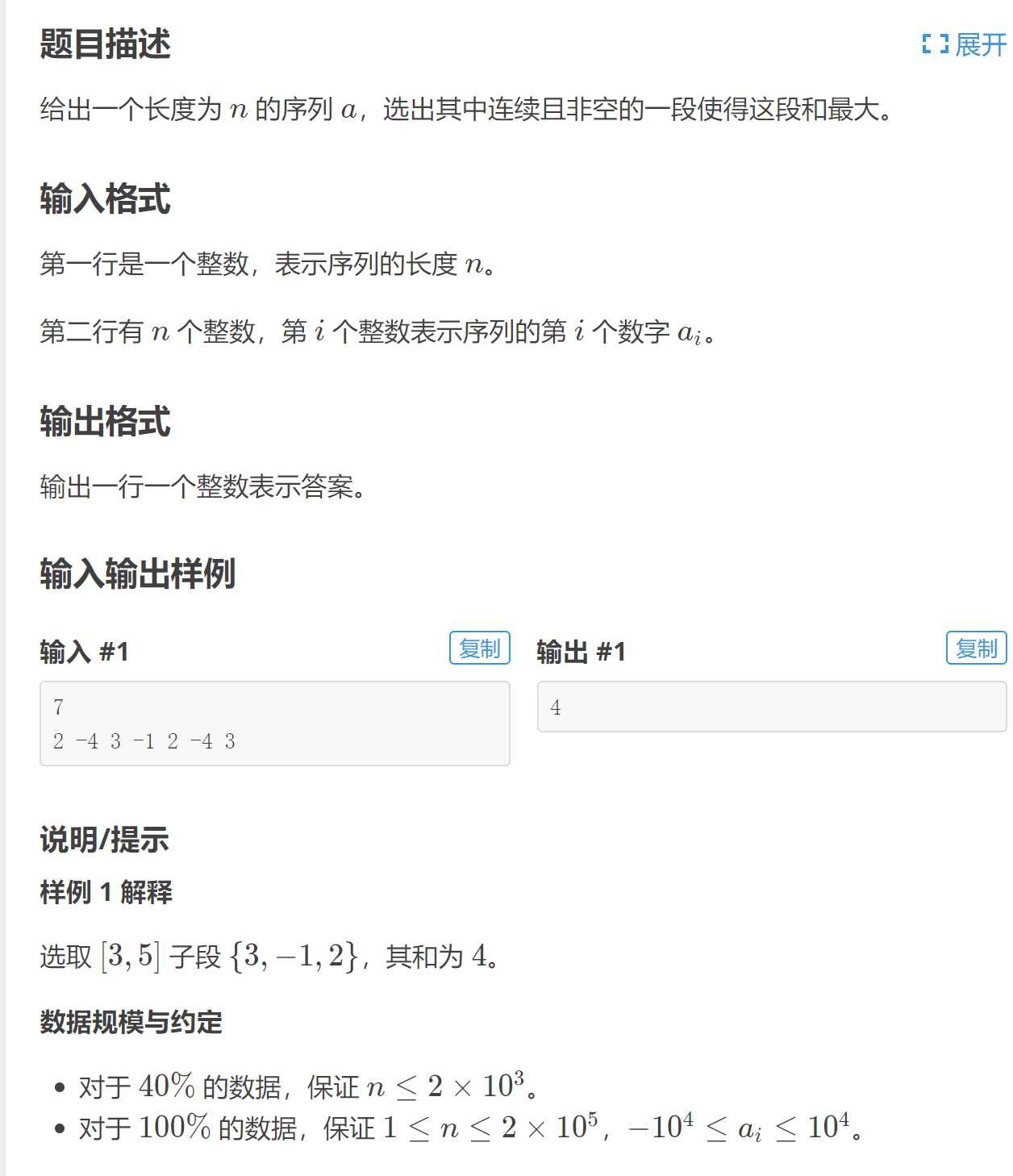
解法一：分治思想

解法二：（暴力模拟）

#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
int a[200200];
int n;
int fun()//两次循环暴力计算
{
　　int sum=0;
　　int maxm=-213113;
　　for(int j=1;j<=n;j++){ //（每一次就相当于从起点开始用了一次擂台法求“和”的最大值）
　　　　for(int i=j;i<=n;i++){
　　　　　　sum+=a[i];
　　　　　　maxm=max(sum,maxm);//maxm在动态变化
　　　　}　　
　　　　sum=0;
　　}
　　return maxm;
}
int main()
{
　　cin>>n;
　　for(int i=1;i<=n;i++)
　　　　cin>>a[i];
　　cout<<fun();
　　return 0;
}

解法三：（贪心算法）

#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
int a[200200];
int n;
int fun() //贪心算法（时间复杂度最低）
{
/* 原理在于：
如果前缀和sum变成了负数，那么下一个数就不需要前面的数了（因为还不如只选它一个）
如果前缀和sum没有成符数，就说明前面所有的前缀元素和是有贡献的，不能抛弃他们*/
　　int sum=0;
　　int maxm=-213113;
　　for(int j=1;j<=n;j++）

　　{

　　　　sum+=a[j];
　　　　if(sum<0)
　　　　　　sum=0;
　　　　maxm=max(sum,maxm);
　　}
　　return maxm;
}
int main()
{
　　cin>>n;
　　for(int i=1;i<=n;i++)
　　　　cin>>a[i];
　　cout<<fun();
　　return 0;
//此题如果出现测试集全为负数的情况就需要开特例处理了
}

题解——最大的和

原文：https://www.cnblogs.com/Hello-world-hello-lazy/p/13526911.html