点分治

点分治是一种处理树上统计问题的算法。
由于代码较长，本文的代码都放在了这里。

静态点分治

先谈一类“静态的”树上路径统计问题（即不对路径进行修改）。
我们通过一道例题来理解它的思路：

\(\mathbf{P4178\;Tree}\)
给一棵有\(N\)个点的无根树，每条边有一个权值，求长度不大于\(K\)的路径数量。

由于本题给出的是无根树，因此可以任选一个节点为根节点而不影响答案。
若选择\(p\)为根，那么对\(p\)而言有两种路径：

1. 经过\(p\)
2. 不经过\(p\)，即包含于\(p\)的子树

其中第二类路径可对\(p\)的子树递归处理，从而转化成第一类路径，因此我们重点来处理第一类路径。
一个显然的性质是路径\((x,y)\)合法，当且仅当

1. \(x\)到\(y\)的距离不大于\(K\)。
2. \(x\)到\(y\)的路径没有重叠。

为处理条件一，可用一遍 DFS 预处理出以\(p\)为根的子树节点到\(p\)的长度，记为\(d\)数组。
如何处理条件二呢？
一种方法是在计算答案时利用容斥原理减去不合法的路径条数（在代码部分的“聪聪可可”一题中使用了这种方法）。
另一种方法是记录每个节点属于\(p\)的哪一棵子树，又称“染色法”，下文采用这种方法。
具体实现上，设\(p\)的子树分别为\(s_1\)~\(s_m\)，并在 DFS 处理\(d\)数组的同时处理出整棵树的节点属于\(p\)的哪一棵子树，记为\(b\)数组（特别地，\(b[p]=p\)）。
那么上述条件可表述为：

1. \(d[x]+d[y]\leqslant K\)
2. \(b[x]\neq b[y]\)

例如下面这条路径合法：

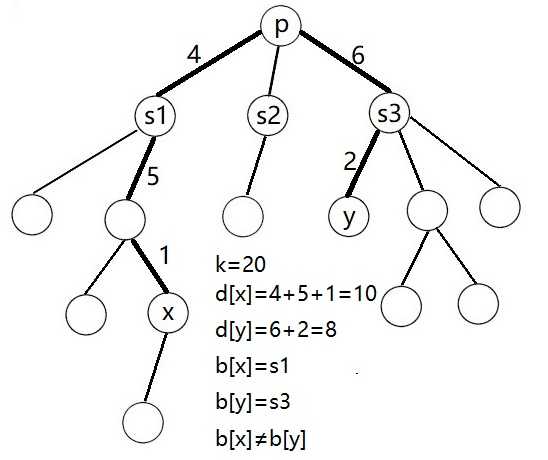
而这条路径由于出现了重叠，所以不合法（不满足条件二）：

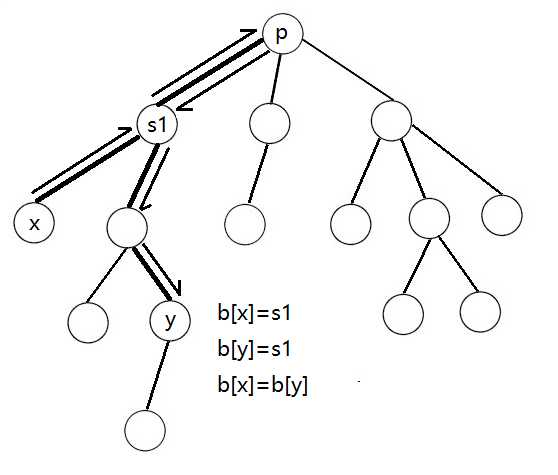
定义\(\operatorname{calc}(p)\)表示以\(p\)为根的树中第一类路径的数量。这个函数有两种常见的实现方式：
方法一：树上直接统计
通俗地说就是利用某种数据结构，直接计数合法点对数量。
在本题中，可以建立一个树状数组维护与\(p\)距离分别为\(0\)~\(K\)的节点个数，依次处理每棵子树\(s_i\)。

1. 对\(s_i\)中的每个\(x\)，如果\(d[x]\leqslant K\)，查询前缀和\(\operatorname{ask}(K-d[x])\)（因为大于\(K\)的\(x\)对答案一定没有贡献），累加进答案，并将答案\(+1\)（就是合法点对的数量，\(+1\)是包括路径\((x,p)\)）。
2. 对\(s_i\)中的每个\(x\)，如果\(d[x]\leqslant K\)，执行\(\operatorname{add}(d[x],1)\)，代表与\(p\)距离\(d[x]\)的节点增加\(1\)。

需注意的是，本题中\(0\leqslant K\leqslant 2\times 10^4\)，因此时间复杂度为\(O(N\log N\log K)\)，可以接受。如果\(K\)过大，那么可以用平衡树来代替，但是代码会更加复杂。
方法二：指针扫描数组
把树上每个点放进一个数组并以d值为关键字排序，用两个指针\(L\)和\(R\)扫描数组。
可以发现，在L从左往右扫时，使\(d[a[L]]+d[a[R]]\leqslant K\)的\(R\)从右往左递减。
我们再用数组\(cntb[s]\)维护\([L,R]\)中满足\(b[a[i]]=s\)的\(i\)的数量。
于是对\(a[L]\)而言，答案就是\([L+1,R]\)中的所有元素的数量减去其中\(b\)值与\(b[a[L]]\)相同的元素（不包括\(a[L]\)）的数量，即\(R-L-cntb[b[a[L]]]+1\)。
每次扫描时检查是否有\(d[a[L]]+d[a[R]]\leqslant K\)，如果是则更新答案，否则左移\(R\)直到满足条件为止。

解决了路径统计的问题，现在来看如何选择根节点\(p\)。
显然\(p\)不能随便选择，如果给出一条链，每次选择链的一端，那么需要分治\(O(N)\)次，会被卡掉。因此我们选择当前树的重心作为根，这样就只至多需要分治\(O(\log N)\)次了。
总结一下点分治的过程：

1. 选择当前树的重心作为根节点\(p\)
2. 从\(p\)出发 DFS，求出\(b\)和\(d\)数组
3. 执行\(\operatorname{calc}(p)\)
4. 删除\(p\)，对\(p\)的子树递归执行\(1\)~\(4\)步。如果\(p\)没有子树，结束递归

点分治的时间复杂度为\(O(N\log^2N)\)。

点分治

原文：https://www.cnblogs.com/LZShuing-xuan/p/13515828.html