如果你看过一些关于组合数学的书,你可能会想到,这种排列计数可以对应到这样的图上:
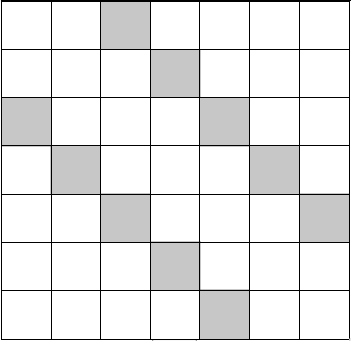
所求的排列个数,就等于在这样的棋盘格子内放 \(n\) 个互不攻击的車,且阴影格子不能放的方案数。上图是 \(n=7,k=2\) 的情况。
这又怎么求呢?考虑容斥。设 \(f_i\) 表示我硬要在阴影里放 \(i\) 个車,剩下随便放的方案数,那么答案等于 \(\sum_{i=0}^n (-1)^if_i(n-i)!\) 。
那现在只要求 \(f_i\) 就好了。
考虑现在的还有什么限制,你发现同一行同一列的阴影格子还是不能同选。把不能同选的格子连上边:
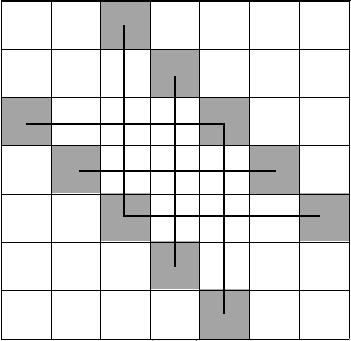
那 \(f_i\) 其实就是这个图大小为 \(i\) 的独立集个数。
很明显这个图就是若干条链。
考虑把这些链连起来。转为求从这一排结点中选 \(i\) 个,拼接的位置可以相邻,其他位置不能相邻 的方案数。于是它变为了一个简单的 DP 问题。
\(O(n^2)\) 解决。
当然这题可以用多项式方法做到 \(O(n\log n)\)。不讲。
原文:https://www.cnblogs.com/Camp-Nou/p/13541493.html