Codeforces Round #529 (Div. 3) F. Make It Connected (贪心,最小生成树)

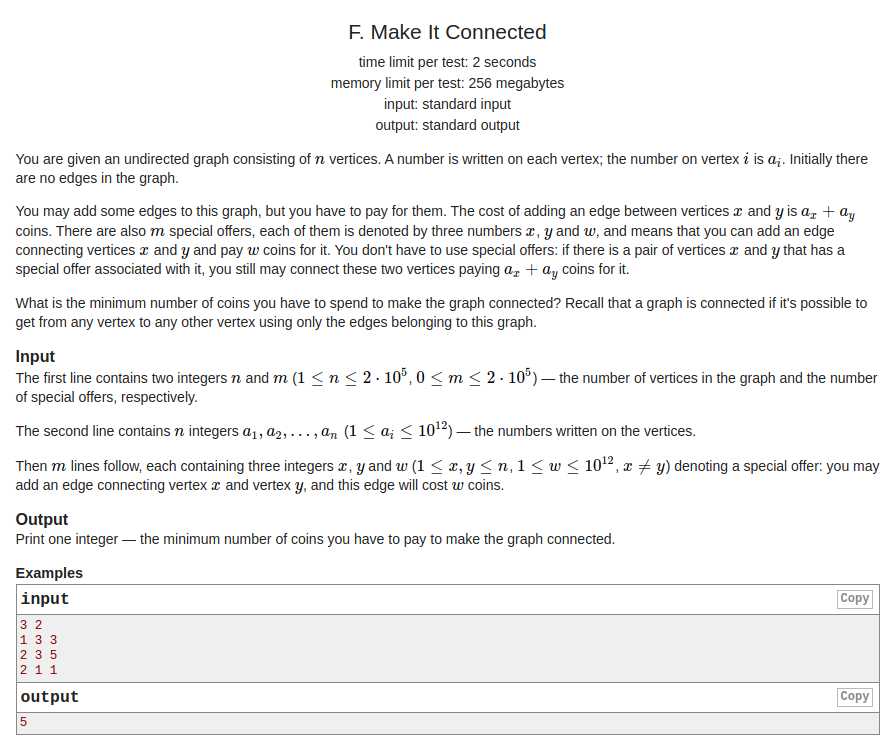
• 题意:给你\(n\)个点,每个点都有权值,现在要在这\(n\)个点中连一颗最小树,每两个点连一条边的边权为两个点的点权,现在还另外给了你几条边和边权,求最小权重.

• 题解:对于刚开始所给的\(n\)个点,假如不考虑后来给的边,仅用这些点来构造,那么最优解一定是最小点权的那个点和其他点连边,所以我们先把这样连边存起来,然后再把加进来的边存起来跑个kruskal求一下就行了.

• 代码:

  struct misaka{
      int a,b;
      ll val;
  }e[N];
   
  int n,m;
  ll a[N];
  int mi;
  int p[N];
   
  bool cmp(misaka x,misaka y){
      return x.val<y.val;
  }
   
  int find(int x){
      if(p[x]!=x) p[x]=find(p[x]);
      return p[x];
  }
   
  int main() {
      //ios::sync_with_stdio(false);cin.tie(0);
      scanf("%d %d",&n,&m);
      a[mi]=1e18;
      for(int i=1;i<=n;++i) p[i]=i;
      for(int i=1;i<=n;++i){
         scanf("%lld",&a[i]);
         if(a[mi]>a[i]) mi=i;
      }
      for(int i=1;i<=m;++i){
          scanf("%d %d %lld",&e[i].a,&e[i].b,&e[i].val);
      }
      for(int i=1;i<=n;++i){
          if(mi==i) continue;
          e[i+m].a=mi;
          e[i+m].b=i;
          e[i+m].val=a[mi]+a[i];
      }
      sort(e+1,e+1+n+m,cmp);
   
      int edge=0;
      ll res=0;
   
      for(int i=1;i<=n+m;++i){
          int a=e[i].a;
          int b=e[i].b;
          ll val=e[i].val;
   
          a=find(a);
          b=find(b);
   
          if(a!=b){
              p[a]=b;
              edge++;
              res+=val;
              if(edge==n-1) break;
          }
      }
   
      printf("%lld\n",res);
   
      return 0;
  }
  

Codeforces Round #529 (Div. 3) F. Make It Connected (贪心,最小生成树)

原文：https://www.cnblogs.com/lr599909928/p/13544033.html