Kernel Principle Component Analysis

• 算法特征:
  ①. 数据中心化; ②. 极大化投影方差; ③. 固定投影矢量长度
• 算法推导:
  Part Ⅰ: PCA
  PCA特征提取方程如下:
  \begin{equation}
  h(x) = W^\mathrm{T}(x - \bar{x})
  \label{eq_1}
  \end{equation}
  其中, $W$为单位投影矢量, $\bar{x} = \sum\limits_{i}x^{(i)} / n$为样本均值.
  PCA原始优化问题如下:
  \begin{equation}
  \begin{split}
  \max\quad &\left\| \frac{A^{\mathrm{T}}W}{\|W\|_2} \right\|_2^2   \\
  \mathrm{s.t.}\quad &\| W \|_2^2 = 1
  \end{split}
  \label{eq_2}
  \end{equation}
  其中, $A = [x^{(1)} - \bar{x}, x^{(2)} - \bar{x}, \cdots, x^{(n)} - \bar{x}]$.
  不失一般性, 将优化问题(\ref{eq_2})等效转换如下:
  \begin{equation}
  \begin{split}
  \min\quad &-\| A^{\mathrm{T}}W \|_2^2   \\
  \mathrm{s.t.}\quad &\| W \|_2^2 = 1
  \end{split}
  \label{eq_3}
  \end{equation}
  根据优化问题(\ref{eq_3})KKT条件中关于原变量$W$的稳定性条件有:
  \begin{equation}
  AA^\mathrm{T}W = \beta W
  \label{eq_4}
  \end{equation}
  其中, $\beta$、$W$分别为协方差矩阵$AA^\mathrm{T}$的本征值与本征矢. 由于$AA^\mathrm{T} \succeq 0$, 有$\beta\geq 0$. 进一步可将优化问题(\ref{eq_3})转换如下:
  \begin{equation}
  \begin{split}
  \max\quad &\beta   \\
  \mathrm{s.t.}\quad &\| W \|_2^2 = 1
  \end{split}
  \label{eq_5}
  \end{equation}
  因此, 所求单位投影矢量$W$即为协方差矩阵$AA^\mathrm{T}$最大本征值$\beta$所对应的本征矢.
  Part Ⅱ: KPCA
  现进行如下变数变换,
  \begin{equation}
  W = A\alpha
  \label{eq_6}
  \end{equation}
  代入式(\ref{eq_4})并左乘$A^\mathrm{T}$有:
  \begin{equation}
  A^\mathrm{T}AA^\mathrm{T}A\alpha = A^\mathrm{T}A\beta\alpha \quad\Rightarrow\quad A^\mathrm{T}A\alpha = \beta\alpha
  \label{eq_7}
  \end{equation}
  为增强模型的特征提取能力, 引入kernel trick, 则式(\ref{eq_7})转换如下:
  \begin{equation}
  K(A^\mathrm{T}, A)\alpha = \beta\alpha
  \label{eq_8}
  \end{equation}
  其中, $K$代表kernel矩阵, 则$\alpha$为此kernel矩阵最大本征值$\beta$所对应的本征矢. 内部元素$K_{ij} = k(x^{(i)}, x^{(j)})$由kernel函数决定. 常见的kernel函数如下:
  ①. 多项式核: $k(x^{(i)}, x^{(j)}) = (x^{(i)}\cdot x^{(j)} + 1)^n$
  ②. 高斯核: $k(x^{(i)}, x^{(j)}) = \mathrm{e}^{-\mu\| x^{(i)} - x^{(j)} \|_2^2}$
  结合式(\ref{eq_1})、式(\ref{eq_6})及kernel trick可得最终特征提取方程:
  \begin{equation}
  h(x) = \alpha^\mathrm{T}K(A^\mathrm{T}, x - \bar{x})
  \label{eq_9}
  \end{equation}
• 代码实现:
  
  

    1 # Kernal Princlple Component Analysis之实现
    2 
    3 import numpy
    4 from matplotlib import pyplot as plt
    5 
    6 numpy.random.seed(0)
    7 
    8 
    9 def getOriData(type1Size=100, type2Size=100):
   10     ‘‘‘
   11     生成特征提取数据集
   12     ‘‘‘
   13     theta1 = numpy.random.uniform(0, 2 * numpy.pi, type1Size)
   14     theta2 = numpy.random.uniform(0, 2 * numpy.pi, type2Size)
   15     
   16     R1 = numpy.random.uniform(0, 0.3, type1Size).reshape((-1, 1))
   17     R2 = numpy.random.uniform(0.7, 1, type2Size).reshape((-1, 1))
   18     X1 = R1 * numpy.hstack((numpy.cos(theta1).reshape((-1, 1)), numpy.sin(theta1).reshape((-1, 1))))
   19     X2 = R2 * numpy.hstack((numpy.cos(theta1).reshape((-1, 1)), numpy.sin(theta1).reshape((-1, 1))))
   20     return X1, X2
   21 
   22 
   23 class KPCA(object):
   24     
   25     def __init__(self, X, mu=1):
   26         ‘‘‘
   27         X: 特征提取数据集, 1行代表1个样本
   28         ‘‘‘
   29         self.__X = X                          # 特征提取数据集
   30         self.__mu = mu                        # gaussian kernel之超参数
   31         
   32         self.__mean = numpy.mean(X, axis=0)
   33         self.__A = (X - self.__mean).T
   34         
   35         
   36     def get_XTra(self, featureCnt=1):
   37         ‘‘‘
   38         获取所有样本特征提取结果
   39         featureCnt: 待提取特征数
   40         ‘‘‘
   41         XTra = list()
   42         for xOri in self.__X:
   43             xTra = self.get_xTra(xOri, featureCnt)
   44             XTra.append(xTra)
   45         XTra = numpy.array(XTra)
   46         return XTra
   47         
   48         
   49     def get_xTra(self, xOri, featureCnt=1):
   50         ‘‘‘
   51         获取指定样本特征提取结果
   52         ‘‘‘
   53         A = self.__A
   54         mu = self.__mu
   55         mean = self.__mean.reshape((-1, 1))
   56         if not hasattr(self, "eigVals"):
   57             KAA = self.__get_KAA(A, mu)
   58             self.__calc_eigs(KAA)
   59         eigVecs = numpy.real(self.eigVecs)
   60         
   61         x = numpy.array(xOri).reshape((-1, 1))
   62         xTra = list()
   63         for i in range(featureCnt):
   64             alpha = eigVecs[:, i:i+1]
   65             hVal = self.__get_hVal(x, mean, alpha, A, mu)
   66             xTra.append(hVal)
   67         xTra = numpy.array(xTra)
   68         return xTra
   69             
   70     
   71     def __get_hVal(self, x, mean, alpha, A, mu):
   72         KAx = self.__get_KAx(A, x - mean, mu)
   73         hVal = numpy.matmul(alpha.T, KAx)[0, 0]
   74         return hVal
   75         
   76     
   77     def __calc_eigs(self, KAA):
   78         oriEigVals, oriEigVecs = numpy.linalg.eig(KAA)
   79         seqArr = numpy.argsort(-oriEigVals)
   80         self.eigVals = oriEigVals[seqArr]
   81         self.eigVecs = oriEigVecs[:, seqArr]
   82     
   83     
   84     def __get_KAx(self, A, x, mu):
   85         KAx = numpy.zeros((A.shape[1], 1))
   86         for rowIdx in range(KAx.shape[0]):
   87             x1 = A[:, rowIdx:rowIdx+1]
   88             val = self.__calc_gaussian(x1, x, mu)
   89             KAx[rowIdx, 0] = val
   90         return KAx
   91     
   92         
   93     def __get_KAA(self, A, mu):
   94         KAA = numpy.zeros((A.shape[1], A.shape[1]))
   95         for rowIdx in range(KAA.shape[0]):
   96             for colIdx in range(rowIdx + 1):
   97                 x1 = A[:, rowIdx:rowIdx+1]
   98                 x2 = A[:, colIdx:colIdx+1]
   99                 val = self.__calc_gaussian(x1, x2, mu)
  100                 KAA[rowIdx, colIdx] = KAA[colIdx, rowIdx] = val
  101         return KAA
  102         
  103         
  104     def __calc_gaussian(self, x1, x2, mu):
  105         val = numpy.math.exp(-mu * numpy.linalg.norm(x1 - x2) ** 2)
  106         # val = (numpy.sum(x1 * x2) + 1)
  107         return val
  108         
  109 
  110 class KPCAPlot(object):
  111     
  112     @classmethod
  113     def show_XTra(cls, X1Ori, X2Ori, mu=1):
  114         XOri = numpy.vstack((X1Ori, X2Ori))
  115         kpcaObj = KPCA(XOri, mu)
  116         XTra = kpcaObj.get_XTra(2)
  117         
  118         X1Tra = XTra[:X1Ori.shape[0], :]
  119         X2Tra = XTra[X1Ori.shape[0]:, :]
  120         
  121         fig = plt.figure(figsize=(10, 3))
  122         ax1 = plt.subplot(1, 2, 1)
  123         ax2 = plt.subplot(1, 2, 2)
  124         
  125         ax1.scatter(X1Ori[:, 0], X1Ori[:, 1], c="red", s=5, label="cluster 0")
  126         ax1.scatter(X2Ori[:, 0], X2Ori[:, 1], c="green", s=5, label="cluster 1")
  127         ax1.set(title="Ori Data", xlabel="$x_1$", ylabel="$x_2$")
  128         
  129         ax2.scatter(X1Tra[:, 0], X1Tra[:, 1], c="red", s=5, label="cluster 0")
  130         ax2.scatter(X2Tra[:, 0], X2Tra[:, 1], c="green", s=5, label="cluster 1")
  131         ax2.set(title="Tra Data", xlabel="$c_1$", ylabel="$c_2$")
  132         
  133         ax1.legend()
  134         ax2.legend()
  135         fig.tight_layout()
  136         fig.savefig("./show_XTra.png", dpi=100)
  137         
  138         
  139 
  140 if __name__ == "__main__":
  141     X1, X2 = getOriData(100, 100)
  142     KPCAPlot.show_XTra(X1, X2, 1)

  View Code
• 结果展示:
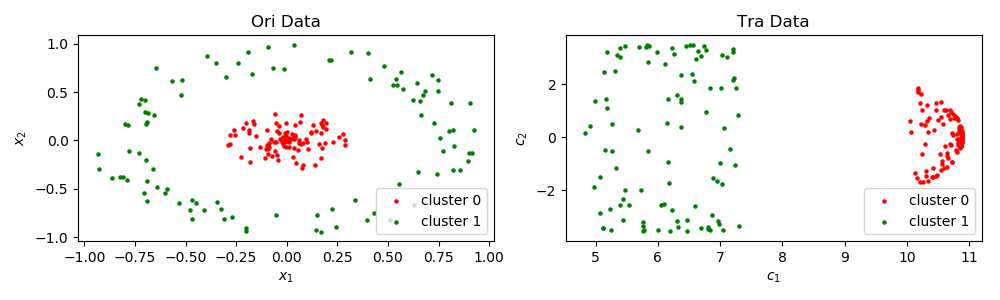  左侧为特征提取数据集分布情况, 右侧为该数据集经过KPCA映射后取前2个主成分的分布情况. 很显然, 在合适的超参数选取下, 经过KPCA映射后, 原始非线性可分的数据集转变为线性可分.
• 使用建议:
  ①. 实对称矩阵不同本征值的本征矢彼此正交.

Kernel Principle Component Analysis

原文：https://www.cnblogs.com/xxhbdk/p/13463888.html