核心思想:
Self-Attention:能注意到输入序列的不同位置以计算该序列的表达能力,类似于textCNN中的卷积核
Encoder-Decoder
多层注意力机制(Scaled dot product attention,Multi-head attention)
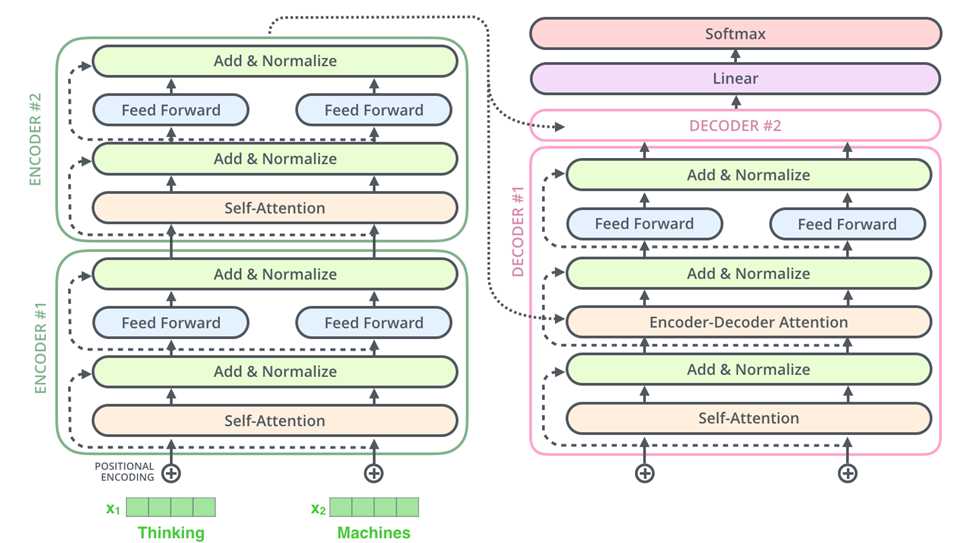
transformer整体模型框架:
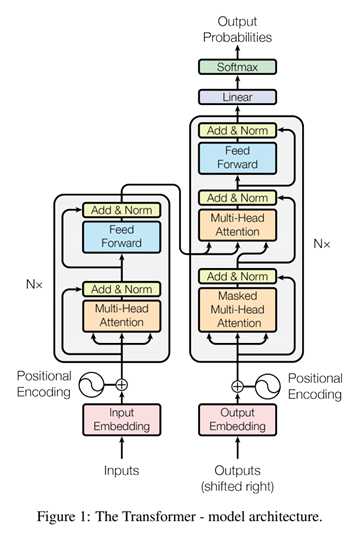
(1)首先,可以看出整个transformer由encoder和decoder两个部分组成,论文中每个编码器和解码器均有6个相同的子组件叠加在一起。
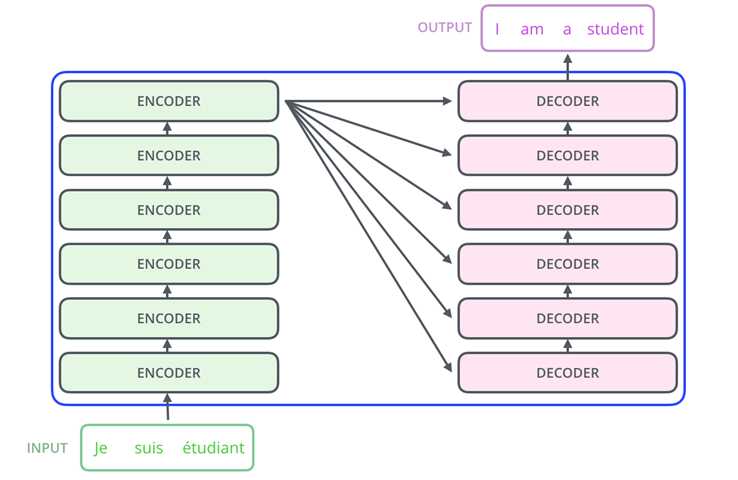
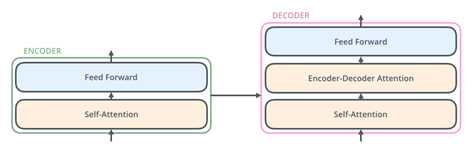
(2)在分开看每个编码器和解码器的结构,每个编码器有以上两层构成,而解码器中间多了一层
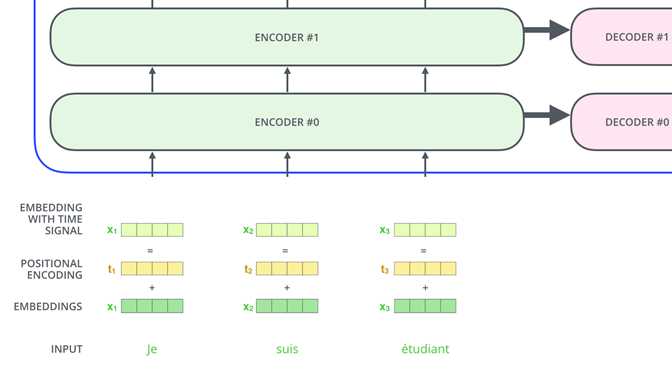
(3)接下来从输入开始看(Input)

positional Encoding:
由于并行输入无法显示时序,输入词嵌入需要加入编码位置
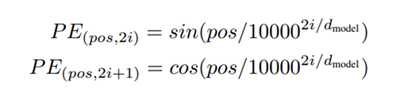
解释一下上面的公式:
pos表示单词在句子中的绝对位置,pos=0,1,2…,例如:Jerry在"Tom chase Jerry"中的pos=2;dmodel表示词向量的维度,在这里dmodel=512;2i和2i+1表示奇偶性,i表示词向量中的第几维,例如这里dmodel=512,故i=0,1,2…255。
至于上面这个公式是怎么得来地,其实不重要,因为很有可能是作者根据经验自己造地,而且公式也不是唯一地,后续goole在bert中的positional encoding也没有再使用这种方法而是通过训练PE,说明这种求位置向量的方法还是存在一定问题地。
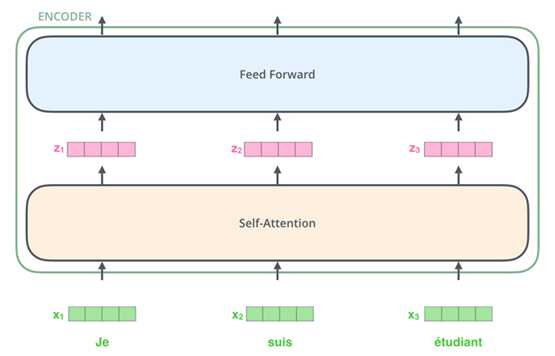
(4)Encoder
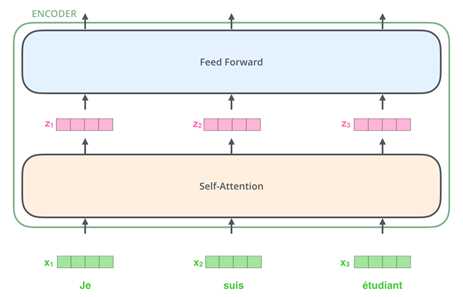
首先每个Encoder有两部分组成,Self - Attention 和 Feed Forward Netural Network
(5)Self-Attention
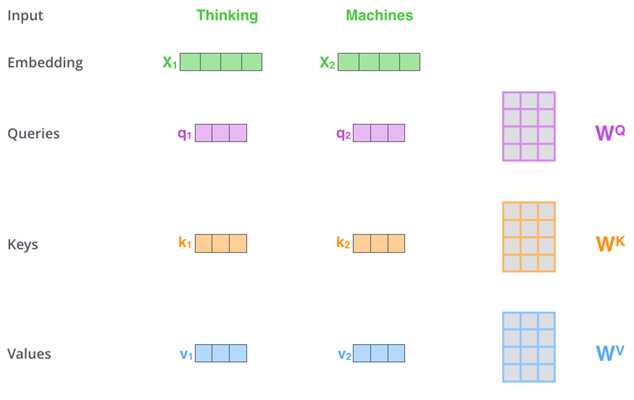
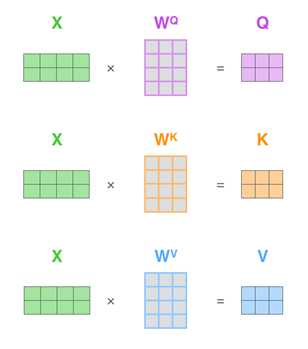
对于进入Self-Attention的每个word, WQ,Wk,Wv是随机初始化的三个矩阵,每个word与三个矩阵相乘,创建三个向量(Query,Key,Value)(64维)
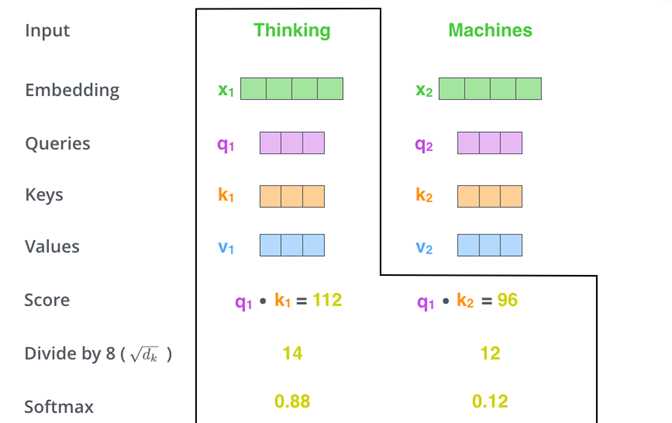
每个q和输入句子中对应的所有k相乘,得到分数score
score除以√64=8
对除完的结果进行softmax标准化
Q:为什么要q,k,v,不像attention一样直接q,v相乘?
如果直接q,v相乘,得到的结果是一个对称矩阵,泛化能力差,只映射到了一个空间上;乘以k,可以映射到不同空间的表示,增加泛化能力
Q:为什么要除以√dk ?
原因一:若q,k相乘结果偏大,进行softmax的话,可能是softmax的值向梯度很小的方向偏
原因二:若q,k~N(0,1),则q*k~N(0,n),除以√dk,可以使方差拉回N(0,1),softmax的值会变得很平缓
总之,为了训练时梯度能够稳定
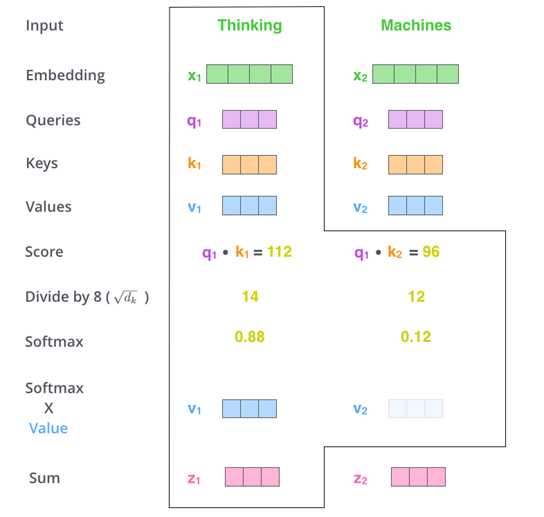
Value乘以softmax结果,sum所有value,产生一个单词的self-attention
实际中,都是矩阵运算,计算Q,K,V矩阵
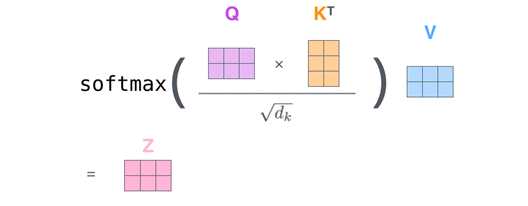
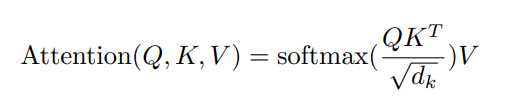
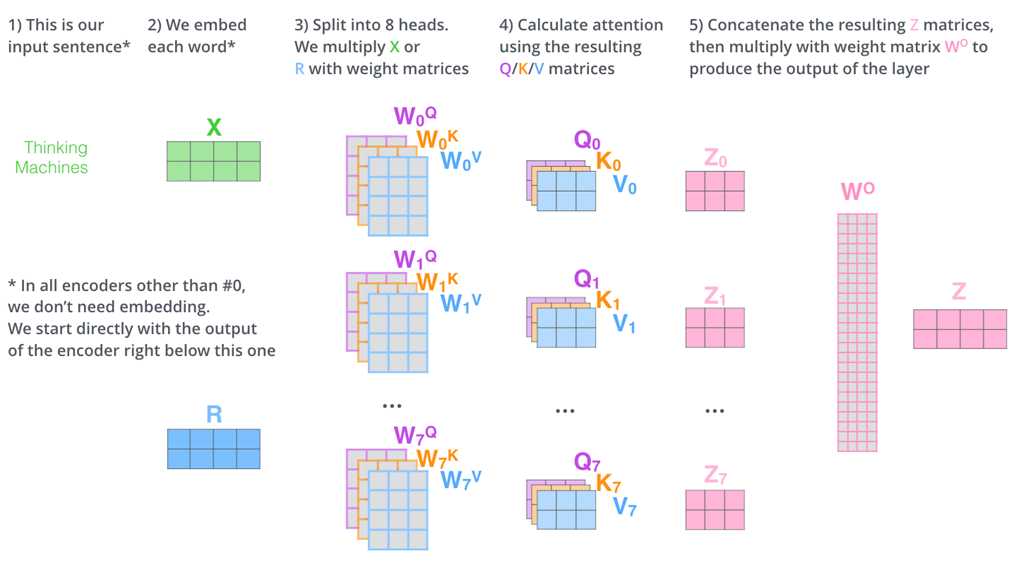
(6)Multi-head Attention:
多头注意力机制就是使用多组WQ,Wk,Wv矩阵计算出多组q,k,v
扩展了关注不同位置的能力;
给与了多个表示子空间;
用不同的权重矩阵做运算,得到不同的Z矩阵
总之,就是得到了多组Z,增加额外的权重矩阵W,进行合并
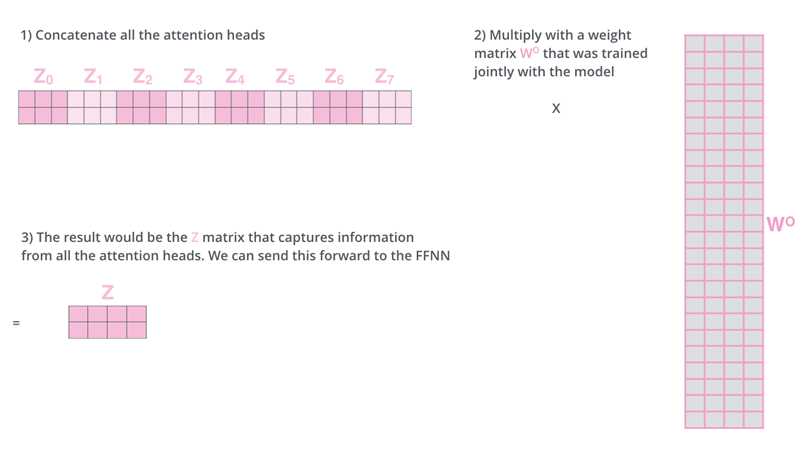
(7)Add&Normalize:
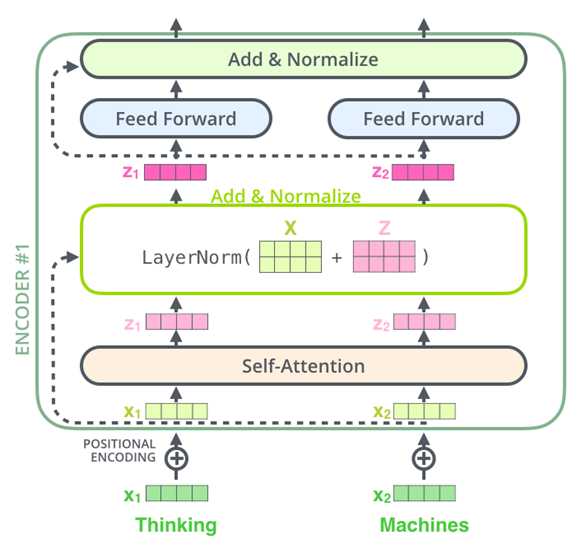
Add
Add,就是在Z的基础上加了一个残差块X,加入残差块X的目的是为了防止在深度神经网络训练中发生退化问题,退化的意思就是深度神经网络通过增加网络的层数,Loss逐渐减小,然后趋于稳定达到饱和,然后再继续增加网络层数,Loss反而增大。为什么深度神经网络会发生退化,为什么添加残差块能够防止退化问题,残差块又是什么?这就牵扯到ResNet残差神经网络的知识了
ResNet 残差神经网络:
首先解答第一个问题,为什么深度神经网络会发生退化?
举个例子:假如某个神经网络的最优网络层数是18层,但是我们在设计的时候并不知道到底多少层是最优解,本着层数越深越好的理念,我们设计了32层,那么32层神经网络中有14层其实是多余地,我们要想达到18层神经网络的最优效果,必须保证这多出来的14层网络必须进行恒等映射,恒等映射的意思就是说,输入什么,输出就是什么,可以理解成F(x)=x这样的函数,因为只有进行了这样的恒等映射咱们才能保证这多出来的14层神经网络不会影响我们最优的效果。
但现实是神经网络的参数都是训练出来地,要想保证训练出来地参数能够很精确的完成F(x)=x的恒等映射其实是很困难地。多余的层数较少还好,对效果不会有很大影响,但多余的层数一多,可能结果就不是很理想了。这个时候大神们就提出了ResNet 残差神经网络来解决神经网络退化的问题。
残差块是什么?

上图就是构造的一个残差块,可以看到X是这一层残差块的输入,也称作F(X)为残差,X为输入值,F(X)是经过第一层线性变化并激活后的输出,该图表示在残差网络中,第二层进行线性变化之后激活之前,F(X)加入了这一层输入值X,然后再进行激活后输出。在第二层输出值激活前加入X,这条路径称作shortcut连接。
为什么添加了残差块能防止神经网络退化问题呢?
咱们再来看看添加了残差块后,咱们之前说的要完成恒等映射的函数变成什么样子了。是不是就变成h(X)=F(X)+X,我们要让h(X)=X,那么是不是相当于只需要让F(X)=0就可以了,这里就巧妙了!神经网络通过训练变成0是比变成X容易很多地,因为大家都知道咱们一般初始化神经网络的参数的时候就是设置的[0,1]之间的随机数嘛。所以经过网络变换后很容易接近于0。
这样当网络自己决定哪些网络层为冗余层时,使用ResNet的网络很大程度上解决了学习恒等映射的问题,用学习残差F(x)=0更新该冗余层的参数来代替学习h(x)=x更新冗余层的参数。
这样当网络自行决定了哪些层为冗余层后,通过学习残差F(x)=0来让该层网络恒等映射上一层的输入,使得有了这些冗余层的网络效果与没有这些冗余层的网络效果相同,这样很大程度上解决了网络的退化问题。
到这里,关于Add中为什么需要加上一个X,要进行残差网络中的shortcut你清楚了吗?Transformer中加上的X也就是Multi-Head Attention的输入,X矩阵。
Normalize
为什么要进行Normalize呢?
在神经网络进行训练之前,都需要对于输入数据进行Normalize归一化,使同一层的数据有相同的分布,这样的话:1,能够加快训练的速度。2.提高训练的稳定性。
为什么使用Layer Normalization(LN)而不使用Batch Normalization(BN)呢?
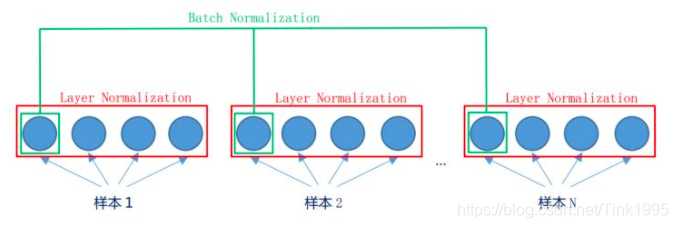
先看图,LN是在同一个样本中不同神经元之间进行归一化,而BN是在同一个batch中不同样本之间的同一位置的神经元之间进行归一化。
BN是对于相同的维度进行归一化,但是咱们NLP中输入的都是词向量,一个300维的词向量,单独去分析它的每一维是没有意义地,在每一维上进行归一化也是适合地,因此这里选用的是LN。
(8)Feed-Forward Networks
全连接层公式如下: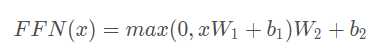
这里的全连接层是一个两层的神经网络,先线性变换,然后ReLU非线性,再线性变换。
这里的x就是我们Multi-Head Attention的输出Z,还是引用上面的例子,那么Z是(2,64)维的矩阵,假设W1是(64,1024),其中W2与W1维度相反(1024,64),那么按照上面的公式:
FFN(Z)=(2,64)x(64,1024)x(1024,64)=(2,64),我们发现维度没有发生变化,这两层网络就是为了将输入的Z映射到更加高维的空间中(2,64)x(64,1024)=(2,1024),然后通过非线性函数ReLU进行筛选,筛选完后再变回原来的维度。
然后经过Add&Normalize,输入下一个encoder中,经过6个encoder后输入到decoder中,至此Transformer的Encoder部分就全部介绍完了
Decoder:
Decoder的输入分为两类:
一种是训练时的输入,一种是预测时的输入。
训练时的输入就是已经对准备好对应的target数据。例如翻译任务,Encoder输入"Tom chase Jerry",Decoder输入"汤姆追逐杰瑞"。
预测时的输入,一开始输入的是起始符,然后每次输入是上一时刻Transformer的输出。例如,输入"",输出"汤姆",输入"汤姆",输出"汤姆追逐",输入"汤姆追逐",输出"汤姆追逐杰瑞",输入"汤姆追逐杰瑞",输出"汤姆追逐杰瑞"结束。
Decoder的attention分为两种,一种是Masked Multi-Head Attention(只关注输出序列中较前位置,mask遮罩),一种是encoder-decoder Attention(自带Query矩阵,Key,Value矩阵来自于编码器)
Masked Multi-Head Attention
与Encoder的Multi-Head Attention计算原理一样,只是多加了一个mask码。mask 表示掩码,它对某些值进行掩盖,使其在参数更新时不产生效果。Transformer 模型里面涉及两种 mask,分别是 padding mask 和 sequence mask。为什么需要添加这两种mask码呢?
1.padding mask
什么是 padding mask 呢?因为每个批次输入序列长度是不一样的也就是说,我们要对输入序列进行对齐。具体来说,就是给在较短的序列后面填充 0。但是如果输入的序列太长,则是截取左边的内容,把多余的直接舍弃。因为这些填充的位置,其实是没什么意义的,所以我们的attention机制不应该把注意力放在这些位置上,所以我们需要进行一些处理。
具体的做法是,把这些位置的值加上一个非常大的负数(负无穷),这样的话,经过 softmax,这些位置的概率就会接近0!
2.sequence mask
sequence mask 是为了使得 decoder 不能看见未来的信息。对于一个序列,在 time_step 为 t 的时刻,我们的解码输出应该只能依赖于 t 时刻之前的输出,而不能依赖 t 之后的输出。因此我们需要想一个办法,把 t 之后的信息给隐藏起来。这在训练的时候有效,因为训练的时候每次我们是将target数据完整输入进decoder中地,预测时不需要,预测的时候我们只能得到前一时刻预测出的输出。
那么具体怎么做呢?也很简单:产生一个上三角矩阵,上三角的值全为0。把这个矩阵作用在每一个序列上,就可以达到我们的目的。
上面可能忘记说了,在Encoder中的Multi-Head Attention也是需要进行mask地,只不过Encoder中只需要padding mask即可,而Decoder中需要padding mask和sequence mask。OK除了这点mask不一样以外,其他的部分均与Encoder一样
Add&Normalize也与Encoder中一样,接下来就到了Decoder中第二个Multi-Head Attention,这个Multi-Head Attention又与Encoder中有一点点不一样。
基于Encoder-Decoder 的Multi-Head Attention
Encoder中的Multi-Head Attention是基于Self-Attention地,Decoder中的第二个Multi-Head Attention就只是基于Attention,它的输入Quer来自于Masked Multi-Head Attention的输出,Keys和Values来自于Encoder中最后一层的输出。
Q:为啥Decoder中要搞两个Multi-Head Attention呢?
我个人理解是第一个Masked Multi-Head Attention是为了得到之前已经预测输出的信息,相当于记录当前时刻的输入之间的信息的意思。第二个Multi-Head Attention是为了通过当前输入的信息得到下一时刻的信息,也就是输出的信息,是为了表示当前的输入与经过encoder提取过的特征向量之间的关系来预测输出。
经过了第二个Multi-Head Attention之后的Feed Forward Network与Encoder中一样,然后就是输出进入下一个decoder,如此经过6层decoder之后到达最后的输出层。
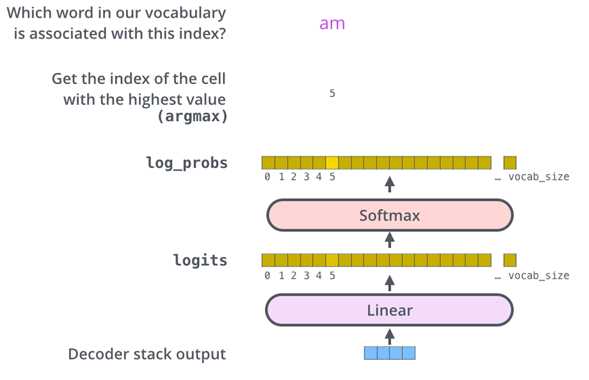
Linear&SoftMax
将输出映射到vocab size维度大小的向量
softmax将得分转化为对应词概率最大的输出
优点:
1.不对数据的时间和空间关系做假设,可以处理一组对象
2.层输出可以并行计算,不像RNN需要序列计算
3.远距离项可以影响彼此输出,无需多步RNN或各种卷积层
4.可以学习长距离的依赖
缺点:
1.对于时间序列,一个单位时间的输出是从整个历史记录计算的,并不是仅从输入和当前的隐含状态得到,可能效率会降低。
2.如果输入数据有时间或空间的关系,则必须加上位置编码,否则模型会有效地看到一堆单词。
https://blog.csdn.net/Tink1995/article/details/105080033/
原文:https://www.cnblogs.com/354151531blogs/p/13550552.html