参考了这篇文章.
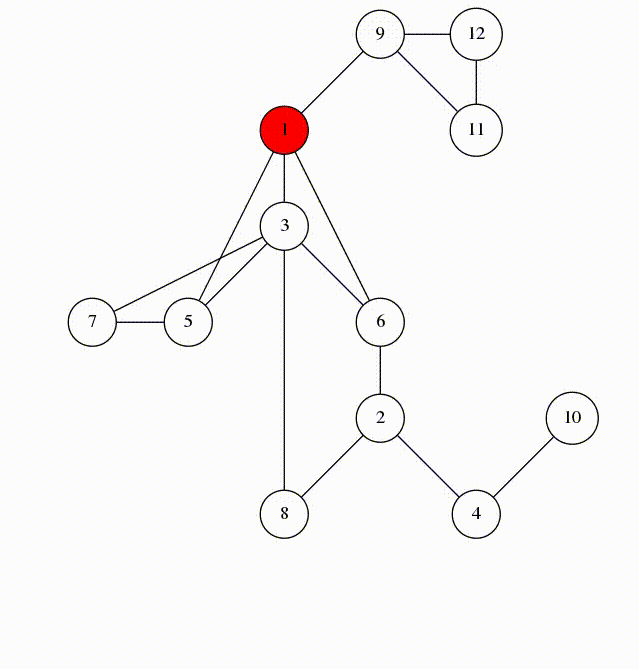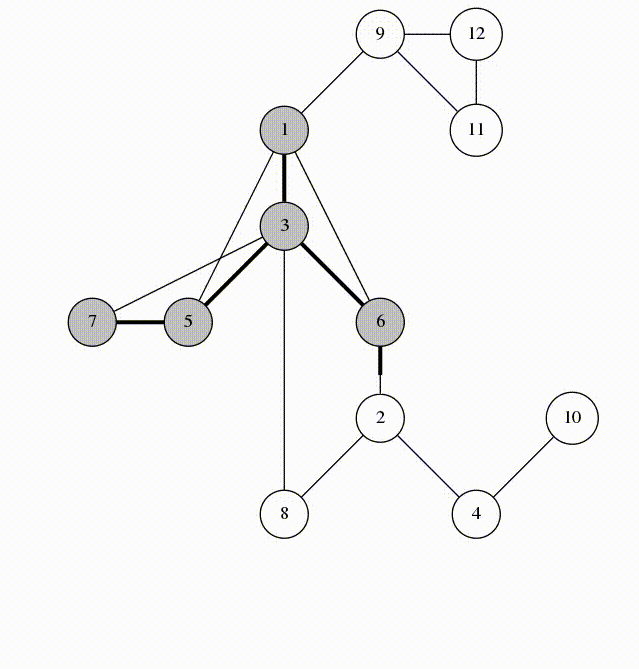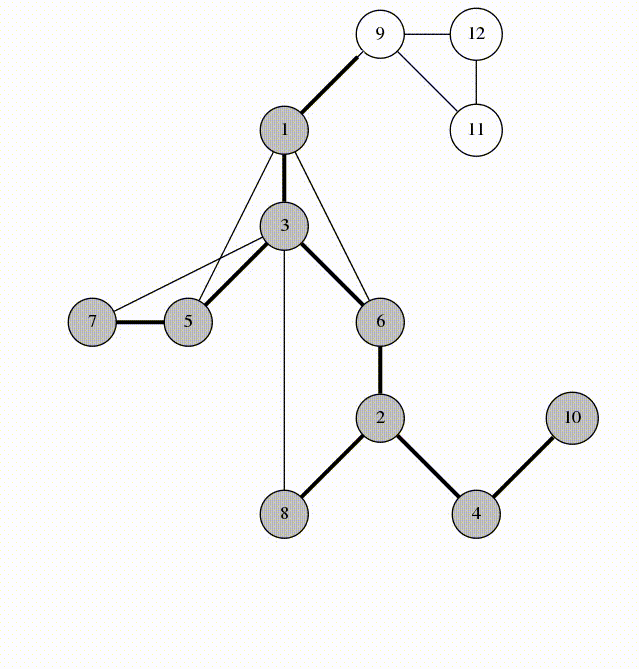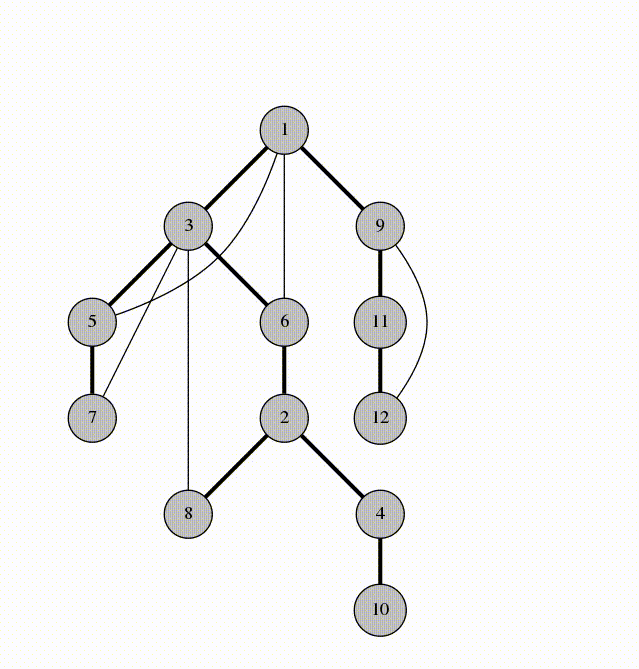
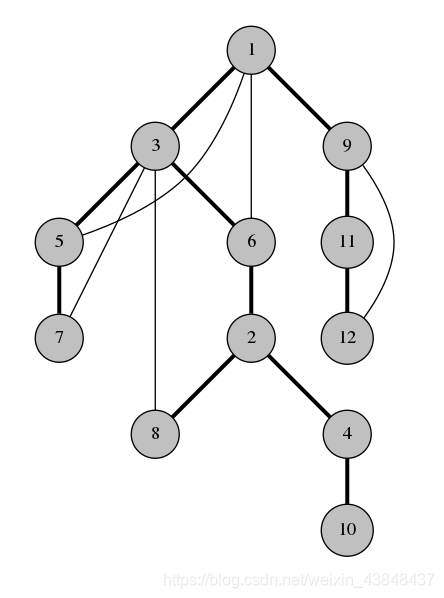
在DFS树上的边称为树边。
对于非树边 \((u,v)\),如果 \(v\) 是 \(u\) 在DFS树上的祖先,称它为后向边;如果 \(v\) 是 \(u\) 在DFS树上的后裔,称它为前向边。
易证,无向图没有横叉边。
非树边一定不是桥。边 \((u,v)\) 是桥,当且仅当 \((u,v)\) 是树边,并且没有非树边跨越这条边。
待续。
设 \(fa\) 是 \(u\) 的父亲,\(dp[u]\) 表示跨越 \(u\) 和它父亲的非树边的数量,则
如果 \(dp[u]=0\),则 \(u\) 和连接DFS树上的它父亲的这条边是桥。
Code
代码是[HDU 4738]这题的一部分,是要求所有桥的边权的最小值,由于无向图没有横叉边,我们可以用DFS的时间戳 \(DFN\) 来判断祖先和后裔的关系。
struct Graph{
struct edge{int Next,to,w;};
edge G[2000010];
int head[1010];
int cnt;
Graph():cnt(2){}
void clear(int node_num=0){
cnt=2;
if(node_num==0) memset(head,0,sizeof(head));
else fill(head,head+node_num+5,0);
}
void add_edge(int u,int v,int w){
G[cnt].w=w;
G[cnt].to=v;
G[cnt].Next=head[u];
head[u]=cnt++;
}
};
Graph G;
int dp[1010],DFN[1010];
bool vis[1010];
int N,M,Index,Ans;
void DFS(int u,int fa,int w,int id){
vis[u]=true;
DFN[u]=++Index;
dp[u]=0;
for(int i=G.head[u];i;i=G.G[i].Next){
int v=G.G[i].to;
if(!vis[v]){DFS(v,u,G.G[i].w,i);dp[u]+=dp[v];}//树边
else if(v!=fa || (v==fa && i!=id && (i^1)!=id)){//非树边,考虑了重边的情况
if(DFN[v]<DFN[u]) ++dp[u];//后向边
else --dp[u];//前向边
}
}
if(dp[u]==0 && fa) Ans=min(Ans,w);//没有非树边跨越u和他父亲,那么这条边是桥
return;
}
原文:https://www.cnblogs.com/AEMShana/p/13551361.html