一般在DL或者一些ML的算法中,在分类的时候,都需要把算法输出值映射到[0-1]的概率空间去,或者在网络内部,神经元激活的时候,都需要一个激活函数。
常见的激活函数有
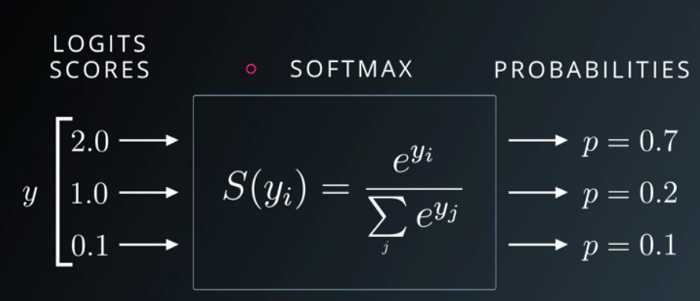
简而言之,softmax就是把一些输出映射为0-1之间的实数,并且归一化保证和为1,因此多分类的概率之和也刚好为1。那么它的计算方式和图上是一致的,logits通常就是我们NN最后一层神经元的输出(不做其他的激活),这个值可大可小,其在最终会被映射到01的概率分布中去,代表每个类被取得的概率。softmax经常是和交叉熵一起使用来计算loss。
因为softmax在多分类上的优越性,所以我们很多树模型像XGB,LGB都是使用softmax来做多分类。GBDT也是可以用类似的思路来实现多分类,LR也是ok的。不过softmax的前提应该是类间是互斥的,就是说每个样本只可能属于一个类。相反的如果类间不互斥的话,那只好采用oneVSreset的思路去做。
Sigmoid也是经常使用的激活函数之一,包括LR,GBDT,XGB和NN内部和2分类时候做激活等。一般树模型的话都是把每棵树最终叶子节点的取值相加后通过sigmoid取得一个概率值之后再去计算loss
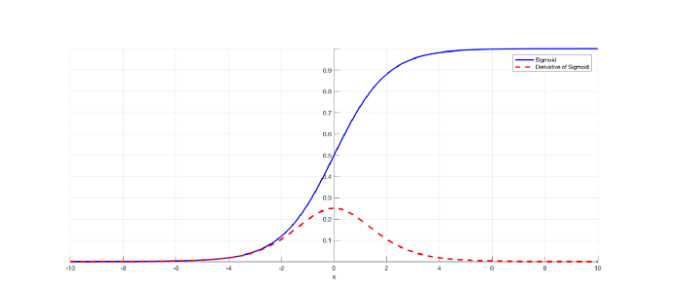
sigmoid虽然有它自己的优点,但是缺点也很明显:导数值最大为0.25,两边无限接近于0,那么这会导致一个问题:当我需要用到sigmoid的导数的时候,如果我输入的值很小或者很大,那么被sigmoid激活后这个值就变得很小。所以很多时候,像NN因为涉及loss的back propagation,链式求导过程中会有求导sigmoid的情况,如果某个权重\(w\)过小,那么就会导致函数值过小,连乘就会越乘越小,所以这个角度上来说,也是NN出现梯度消失的原因。那么梯度爆炸也是差不多的思路,从公式的角度解释就是:
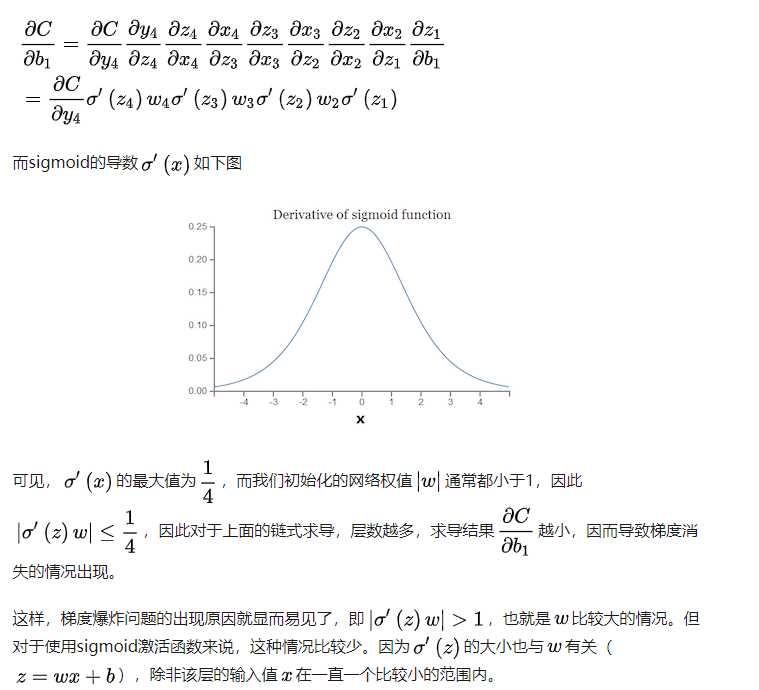
另外一个是像在LR上,LR的对数似然损失或者说二分类交叉熵损失在求导之后,还好sigmoid函数被保留而没有涉及到被求导,不然也会出现就是说loss很小,难以学习的情况。
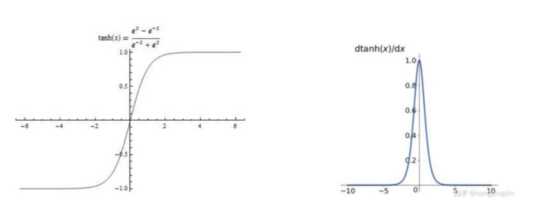
Tanh虽然值域比sigmoid大了很多,但还是会有梯度消失的情况出现
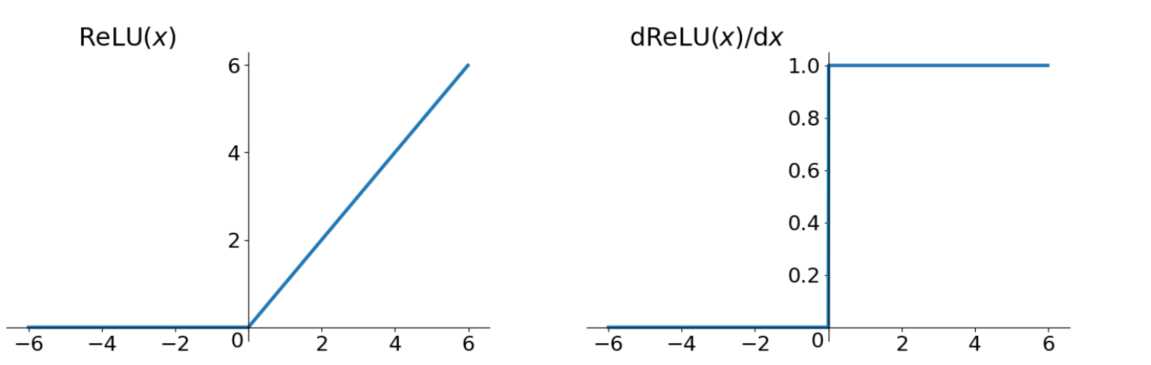
Relu在负向上,也是存在有上面说到的弊端,但已经好很多了
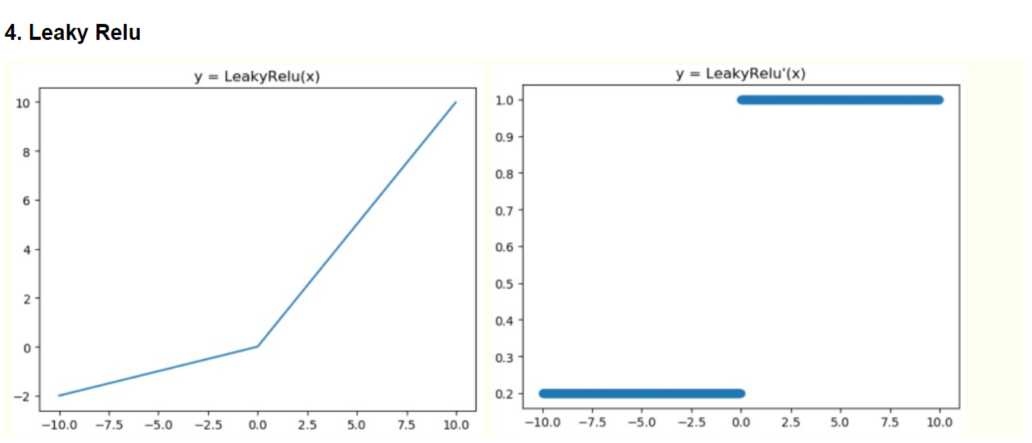
Leakly Relu一般来说,与上面的情况相比,一般不会出现梯度消失的问题
原文:https://www.cnblogs.com/zhouyc/p/13551508.html