用法如下:
class sklearn.svm.SVC(*, C=1.0, kernel=‘rbf‘, degree=3, gamma=‘scale‘, coef0=0.0, shrinking=True, probability=False, tol=0.001, cache_size=200, class_weight=None, verbose=False, max_iter=-1, decision_function_shape=‘ovr‘, break_ties=False, random_state=None)
可选参数
可选标签
数据准备:
# 引入数据 from sklearn import datasets import numpy as np iris = datasets.load_iris() X = iris.data[:,[2,3]] y = iris.target print("Class labels:",np.unique(y)) #打印分类类别的种类 # 切分训练数据和测试数据 from sklearn.model_selection import train_test_split ## 30%测试数据,70%训练数据,stratify=y表示训练数据和测试数据具有相同的类别比例 X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.3,random_state=1,stratify=y) from sklearn.preprocessing import StandardScaler sc = StandardScaler() ## 估算训练数据中的mu和sigma sc.fit(X_train) ## 使用训练数据中的mu和sigma对数据进行标准化 X_train_std = sc.transform(X_train) X_test_std = sc.transform(X_test) ## 画出决策边界图(只有在2个特征才能画出来) import matplotlib.pyplot as plt %matplotlib inline from matplotlib.colors import ListedColormap def plot_decision_region(X,y,classifier,resolution=0.02): markers = (‘s‘,‘x‘,‘o‘,‘^‘,‘v‘) colors = (‘red‘,‘blue‘,‘lightgreen‘,‘gray‘,‘cyan‘) cmap = ListedColormap(colors[:len(np.unique(y))]) # plot the decision surface x1_min,x1_max = X[:,0].min()-1,X[:,0].max()+1 x2_min,x2_max = X[:,1].min()-1,X[:,1].max()+1 xx1,xx2 = np.meshgrid(np.arange(x1_min,x1_max,resolution), np.arange(x2_min,x2_max,resolution)) Z = classifier.predict(np.array([xx1.ravel(),xx2.ravel()]).T) Z = Z.reshape(xx1.shape) plt.contourf(xx1,xx2,Z,alpha=0.3,cmap=cmap) plt.xlim(xx1.min(),xx1.max()) plt.ylim(xx2.min(),xx2.max()) # plot class samples for idx,cl in enumerate(np.unique(y)): plt.scatter(x=X[y==cl,0], y = X[y==cl,1], alpha=0.8, c=colors[idx], marker = markers[idx], label=cl, edgecolors=‘black‘)
线性支持向量机:
## 线性支持向量机 from sklearn.svm import SVC svm = SVC(kernel=‘linear‘,C=1.0,random_state=1) svm.fit(X_train_std,y_train) plot_decision_region(X_train_std,y_train,classifier=svm,resolution=0.02) plt.xlabel(‘petal length [standardized]‘) plt.ylabel(‘petal width [standardized]‘) plt.legend(loc=‘upper left‘) plt.show()
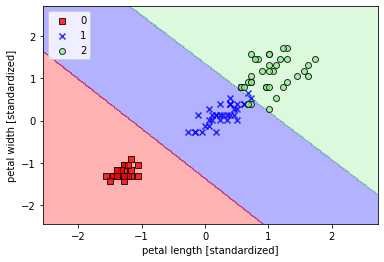
使用核函数对非线性分类问题建模(gamma=0.20)
## 使用核函数对非线性分类问题建模(gamma=0.20) svm = SVC(kernel=‘rbf‘,random_state=1,gamma=0.20,C=1.0) ##较小的gamma有较松的决策边界 svm.fit(X_train_std,y_train) plot_decision_region(X_train_std,y_train,classifier=svm,resolution=0.02) plt.xlabel(‘petal length [standardized]‘) plt.ylabel(‘petal width [standardized]‘) plt.legend(loc=‘upper left‘) plt.show()
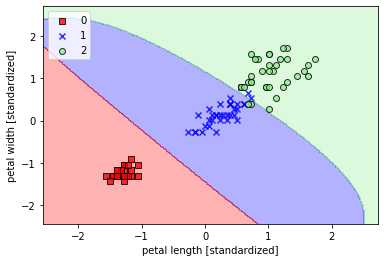
使用核函数对非线性分类问题建模(gamma=100)
## 使用核函数对非线性分类问题建模(gamma=100) svm = SVC(kernel=‘rbf‘,random_state=1,gamma=100.0,C=1.0,verbose=1) svm.fit(X_train_std,y_train) plot_decision_region(X_train_std,y_train,classifier=svm,resolution=0.02) plt.xlabel(‘petal length [standardized]‘) plt.ylabel(‘petal width [standardized]‘) plt.legend(loc=‘upper left‘) plt.show()
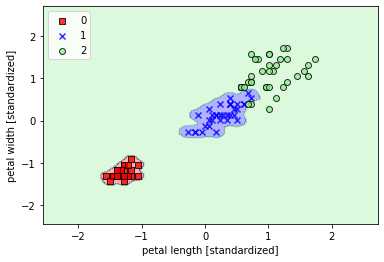
从不同的gamma取值的图像来看:对于高斯核函数,增大gamma值,将增大训练样本的影响范围,导致决策边界紧缩和波动;较小的gamma值得到的决策边界相对宽松。虽然较大的gamma值在训练样本中有很小的训练误差,但是很可能泛化能力较差,容易出现过拟合
全部代码(已折叠)
# -*- coding: utf-8 -*- """ Created on Tue Aug 11 10:12:48 2020 @author: Admin """ # 引入数据 from sklearn import datasets import numpy as np iris = datasets.load_iris() X = iris.data[:,[2,3]] y = iris.target print("Class labels:",np.unique(y)) #打印分类类别的种类 # 切分训练数据和测试数据 from sklearn.model_selection import train_test_split ## 30%测试数据,70%训练数据,stratify=y表示训练数据和测试数据具有相同的类别比例 X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.3,random_state=1,stratify=y) from sklearn.preprocessing import StandardScaler sc = StandardScaler() ## 估算训练数据中的mu和sigma sc.fit(X_train) ## 使用训练数据中的mu和sigma对数据进行标准化 X_train_std = sc.transform(X_train) X_test_std = sc.transform(X_test) ## 画出决策边界图(只有在2个特征才能画出来) import matplotlib.pyplot as plt %matplotlib inline from matplotlib.colors import ListedColormap def plot_decision_region(X,y,classifier,resolution=0.02): markers = (‘s‘,‘x‘,‘o‘,‘^‘,‘v‘) colors = (‘red‘,‘blue‘,‘lightgreen‘,‘gray‘,‘cyan‘) cmap = ListedColormap(colors[:len(np.unique(y))]) # plot the decision surface x1_min,x1_max = X[:,0].min()-1,X[:,0].max()+1 x2_min,x2_max = X[:,1].min()-1,X[:,1].max()+1 xx1,xx2 = np.meshgrid(np.arange(x1_min,x1_max,resolution), np.arange(x2_min,x2_max,resolution)) Z = classifier.predict(np.array([xx1.ravel(),xx2.ravel()]).T) Z = Z.reshape(xx1.shape) plt.contourf(xx1,xx2,Z,alpha=0.3,cmap=cmap) plt.xlim(xx1.min(),xx1.max()) plt.ylim(xx2.min(),xx2.max()) # plot class samples for idx,cl in enumerate(np.unique(y)): plt.scatter(x=X[y==cl,0], y = X[y==cl,1], alpha=0.8, c=colors[idx], marker = markers[idx], label=cl, edgecolors=‘black‘) ## 线性支持向量机 from sklearn.svm import SVC svm = SVC(kernel=‘linear‘,C=1.0,random_state=1) svm.fit(X_train_std,y_train) plot_decision_region(X_train_std,y_train,classifier=svm,resolution=0.02) plt.xlabel(‘petal length [standardized]‘) plt.ylabel(‘petal width [standardized]‘) plt.legend(loc=‘upper left‘) plt.show() ## 使用核函数对非线性分类问题建模(gamma=0.20) svm = SVC(kernel=‘rbf‘,random_state=1,gamma=0.20,C=1.0) ##较小的gamma有较松的决策边界 svm.fit(X_train_std,y_train) plot_decision_region(X_train_std,y_train,classifier=svm,resolution=0.02) plt.xlabel(‘petal length [standardized]‘) plt.ylabel(‘petal width [standardized]‘) plt.legend(loc=‘upper left‘) plt.show() ## 使用核函数对非线性分类问题建模(gamma=100) svm = SVC(kernel=‘rbf‘,random_state=1,gamma=100.0,C=1.0,verbose=1) svm.fit(X_train_std,y_train) plot_decision_region(X_train_std,y_train,classifier=svm,resolution=0.02) plt.xlabel(‘petal length [standardized]‘) plt.ylabel(‘petal width [standardized]‘) plt.legend(loc=‘upper left‘) plt.show()
原文:https://www.cnblogs.com/cgmcoding/p/13559984.html