面试题38：字符串的排列

1 题目描述

??输入一个字符串,按字典序打印出该字符串中字符的所有排列。例如输入字符串abc,则按字典序打印出由字符a,b,c所能排列出来的所有字符串abc,acb,bac,bca,cab和cba。

2 输入

str

3 输出

str的全排列(可能有字符重复)。字符只包括大小写字母。

4 样例输入

"abc"

5 样例输出

"abc", "acb", "bac", "bca", "cab", "cba"

6 求解思路

??牛客题解说到了可以用set集合来存储全排列，不仅帮我解决了重复的排列，而且还帮我拍了个序，秒啊！剩下的就剩下全排列的简单问题了。

7 C++版本代码如下

class Solution {
public:
    
    void mySwap(string &str, int i, int j){
        char temp = str[j];
        str[j] = str[i];
        str[i] = temp;
    }
    
    void dfs(string str, int pos, set<string> &ret){
        if(pos == str.length() - 1){
            ret.insert(str);
            return ;
        }
        for(int i = pos; i < str.length(); i++){
            // 选择这一步决策
            mySwap(str, i, pos);
            // 进入下一个决策树
            dfs(str, pos + 1, ret);
            // 取消这一步决策
            mySwap(str, i, pos);
        }
    }
    
    vector<string> Permutation(string str) {
        if(str.empty())
            return {};
        set<string> ret;
        dfs(str, 0, ret);
        vector<string> ans(ret.begin(), ret.end());
        return ans;
    }
};

??今天补一下另一个版本的求全排列方法。这个方法不会用到交换数字的操作，而且求出的全排列是也是按照字典序排序的。可以说是回溯法的最佳体验了。直接上代码！

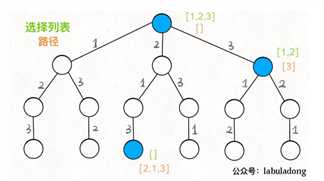
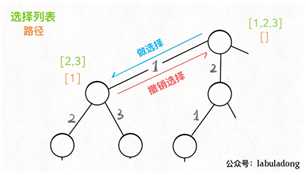
public void permutation(int num[]){
	LinkedList<Integer> track = new LinkedList<>();
    backTrack(num, track);
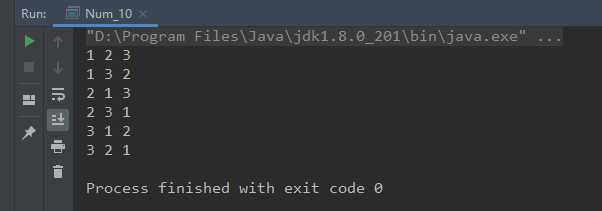
    for(int i = 0; i < res.size(); i++){
        for(int j = 0; j < res.get(i).size(); j++)
            System.out.print(res.get(i).get(j) + " ");
        System.out.println();
    }
}

public void backTrack(int num[], LinkedList<Integer> track){
    if(track.size() == num.length){
        res.add(new LinkedList(track));
        return ;
    }
    for(int i = 0; i < num.length; i++){
        if(track.contains(num[i]))
            continue;
        // 做这一层的决策
        track.add(num[i]);
        // 进入下一层决策树
        backTrack(num, track);
        // 取消这一层的决策
        track.removeLast();
    }
}

面试题38：字符串的排列

原文：https://www.cnblogs.com/flyingrun/p/13565877.html