在OI中学了好几个Tarjan算法,敬佩之情油然而出,今天来了解一下他提出了哪些算法,来个一网打尽,学到屠龙之术QWQ~。
算法1:Tarjan求强连通分量
这个算是Tarjan中最基础的算法了 (反正我的第一个就是这个QAQ)。主要用途为判环和缩点,在很多图论题中都可以使用。
前置芝士:
强连通:如果两个顶点可以相互通达,则称两个顶点 强连通。
强连通图:如果有向图\(G\)的每两个顶点都 强连通,称\(G\)是一个强连通图。
强连通分量:非强连通图有向图的极大强连通子图,称为强连通分量。
然后我们就可以开始学习Tarjan算法啦!
Tarjan算法基于DFS (相信我应该不用再解释)和数据结构栈,通过搜索每一个子树来维护两个数组\(dfn[]\)与\(low[]\)(下面解释),从而查找强连通分量。
现在我们引入两个在Tarjan算法中非常重要的两个数组:
dfn[u]:节点\(u\)搜索的次序编号(时间戳)
low[u]:\(u\)或\(u\)的子树能够追溯到的最早的栈中节点的次序号。
Tarjan算法的过程就是,每次将DFS到的点加入栈中,然后判断出边到达的节点是否在栈中,如果是,则\(low[u]=min(low[u],dfn[v])\)。而当自己这棵子树跑完了之后,发现\(dfn[u]==low[u]\),就说明\(u\)的子节点到达不了时间戳比\(u\)更早的点,所以\(u\)的子树中已经成环,所以打上标记。(注意:每次DFS到一个节点时,需要将\(low[]\)值附成\(dfn[]\)的值)

我们来模拟一下过程
首先DFS到\(1\),所以\(dfn[1]=low[1]=1\),并把\(1\)加入栈中。
栈中:\(1\)
然后DFS到\(2\),\(dfn[2]=low[2]=2\),并把\(2\)加入栈中。
栈中:\(1,2\)
DFS到\(5\),\(dfn[5]=low[5]=3\),并把\(5\)加入栈中。
栈中:\(1,2,5\)
DFS到\(7\),\(dfn[7]=low[7]=4\),并把\(7\)加入栈中。
栈中:\(1,2,5,7\)
这时回溯时发现\(dfn[7]==low[7]\),所以把栈顶到\(7\)归为一个强连通分量,即{\(7\)}本身是一个强连通分量。
继续DFS到\(4\),\(dfn[4]=low[4]=5\),并把\(4\)加入栈中。
栈中:\(1,2,5,4\)
下一条边指向\(1\),发现已经在栈中,于是把\(low[4]=min(low[4],dfn[1])\),因此\(low[4]=1\)。
......
以此类推,最后栈中为{\(1,2,5,4,3\)},发现\(dfn[1]==low[1]\),故将栈顶至\(1\)归为一个强连通分量,说明{\(1,2,5,4,3\)}互相连通。
至此算法结束
模板代码如下:(可以结合代码理解)
#include<bits/stdc++.h>
#define re register
using namespace std;
const int N=10005,M=50005;
inline int read()
{
re int x=0,f=1;
re char ch=getchar();
for(;ch>‘9‘||ch<‘0‘;ch=getchar())if(ch==‘-‘)f*=-1;
for(;ch>=‘0‘&&ch<=‘9‘;ch=getchar())x=(x<<1)+(x<<3)+(ch^48);
return x*f;
}
struct edge{int v,net;}e[M];
int ans,n,m,tim,cnt,hd[N],dfn[N],low[N],st[N],top,col,color[N],num[N];
bool yor[N],vis[N];
inline void add(int v,int u){e[++cnt].v=v,e[cnt].net=hd[u],hd[u]=cnt;}
void Tarjan(int u)
{
yor[u]=vis[u]=1;\\yor[]说明已经到达过该节点,vis[]说明已经入栈
dfn[u]=low[u]=++tim;\\更新时间戳
st[++top]=u;\\入栈
for(re int v,i=hd[u];i;i=e[i].net)
{
v=e[i].v;
if(dfn[v]==0)
{
Tarjan(v);\\继续DFS
low[u]=min(low[u],low[v]);\\可能子节点能达到更早的节点
}
else if(vis[v])
low[u]=min(low[u],dfn[v]);\\更新low[u]
}
if(dfn[u]==low[u])
{
++col;
for(;st[top]!=u;color[st[top]]=col,vis[st[top--]]=0);\\将栈顶到u归为一个强连通分量
color[st[top]]=col,vis[st[top--]]=0;\\弹出栈顶
}
}
int main()
{
scanf("%d%d",&n,&m);
for(re int i=1;i<=m;i++)add(read(),read());
for(re int i=1;i<=n;i++)
if(yor[i]==0)Tarjan(i);//可能整个图不是连通图,要每个点都判断
return 0;
}
算法2:Tarjan求最近公共祖先(LCA)
相信大家应该都已经学过倍增求LCA,是一个在线算法,\(O(n)\)预处理后每次询问时间复杂度为\(O(log^2n)\)。我们今天来谈谈一个离线求LCA的方法:Tarjan算法。
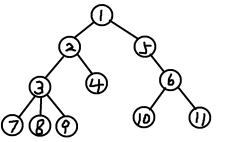
如这张图:
假如我们的询问为:
\((5,7),(4,8),(8,10),(9,1),(10,11)\)
首先我们把询问复制一遍:
\((5,7),(7,5),(4,8),(8,4),(8,10),(10,8),(9,1),(1,9),(10,11),(11,10)\)
至于为什么要复制一遍等后面再讲。
然后我们把与每个点相关的询问加入一个链表中:
如:与\(8\)有关的询问有\((8,4),(8,10)\),\(8\)的链表就为\(4->10\)
然后就可以开始DFS了:
首先从\(1\)开始,发现与\(1\)有关的询问有\((1,10)\),但\(10\)没有访问到,丢一边不管,继续
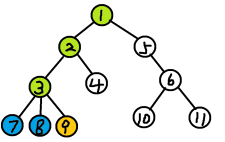
直到如上图,和\(9\)有关的询问有\((9,1)\),而这时候\(1\)已经被访问过了,我们就找绿色节点(被访问过且未回溯的点),这个点要是\(1\)的最大深度的祖先节点(可以是自己),这个节点就是它们的LCA,很明显就是\(1\)。
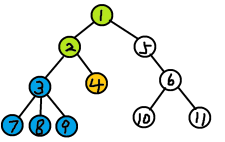
咱们继续,又访问到节点\(4\),发现也有与之相关的询问\((4,8)\),于是找节点\(8\)的深度最大的绿色祖先节点,发现是\(2\),因此\(2\)就是\((4,8)\)的LCA。
......
然后我们就可以离线求出所有的询问答案了!时间复杂度为\(O(n+q)\)。
但有一个问题,怎么找出节点\(8\)的深度最大的绿色祖先节点?我们可以在回溯的时候设一个数组\(f[8]=3\),然后\(3\)回溯时\(f[3]=2\),这样就可以通过并查集的方式\(O(n)\),处理完所有的节点了!QAQ
至此算法结束
代码就不放了,留给大家自己思考 (其实就是懒
算法三:Tarjan求割点和桥:咕咕咕~~
累了,下次再来填这个坑吧。。。
Tarjan算法浅谈
原文:https://www.cnblogs.com/jkzcr01-QAQ/p/13575207.html



