The article aims to describe a solution to leetcode 295.
Problem:
Median is the middle value in an ordered integer list. If the size of the list is even, there is no middle value. So the median is the mean of the two middle value.
Design a data structure that supports the following two operations:
First let‘s examine what property median has.

In the above sorted array, median is 6 in the middle. We can see that 6 is the largest number in the left part (contained in dashed rectangle).

And we can see that 6 is the smallest number in the right part (in the red dashed rectangle). Also all members of left part are less than or equal to all members of right.
Here in a data stream scenario, we could apply a heap data structure. See the description below:
Given such a data structure, we could get the median in a stream in O(1) at any given time.
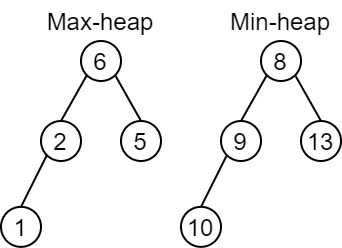
For instance we know the median in the above graph is (6+8)/2=7.0.
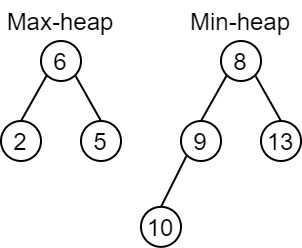
And the median of the above graph is 8.
How to make sure that the sizes of two heaps differ by 1 at most? If currently they have same size, we could insert a new number into one arbitrarily. If their sizes already differ by 1 now, we are able to insert new number into the heap with smaller size if it doesn‘t violate the property that all numbers in max-heap are less than or equal to numbers in min-heap. Otherwise, remove the top element from the heap with larger size and put it in the other heap, and then insert the new number into it.
The code is as follows, the heap is called PriorityQueue in java.
class MedianFinder { private Queue<Integer> L; private Queue<Integer> R; private int s1; private int s2; private class Comp implements Comparator<Integer> { public int compare(Integer i1,Integer i2){ int a=i1.intValue(); int b=i2.intValue(); if(a>b)return -1; if(a==b)return 0; return 1; } } public MedianFinder() { s1=0;s2=0; L=new PriorityQueue<Integer>(new Comp()); R=new PriorityQueue<Integer>(); } public void addNum(int num) { if(s1==s2){ if(s1==0){ L.offer(num); s1++; } else { if(num<=L.peek().intValue()){ L.offer(num); s1++; } else { R.offer(num); s2++; } } } else if(s1<s2){ if(num<=R.peek().intValue()){ L.offer(num); s1++; } else { R.offer(num); L.offer(R.poll()); s1++; } } else { if(num>=L.peek().intValue()){ R.offer(num); s2++; } else { L.offer(num); R.offer(L.poll()); s2++; } } } public double findMedian() { if(s1>s2)return (double)L.peek().intValue(); if(s1<s2)return (double)R.peek().intValue(); int l=L.peek(); int r=R.peek(); return (l+r)/2.0; } }
Applying heap to find median in a stream
原文:https://www.cnblogs.com/shepherdgai/p/13579848.html