BFS:广度优先遍历,类似于层次遍历,一层一层往下走。
BFS的实现借助于队列:
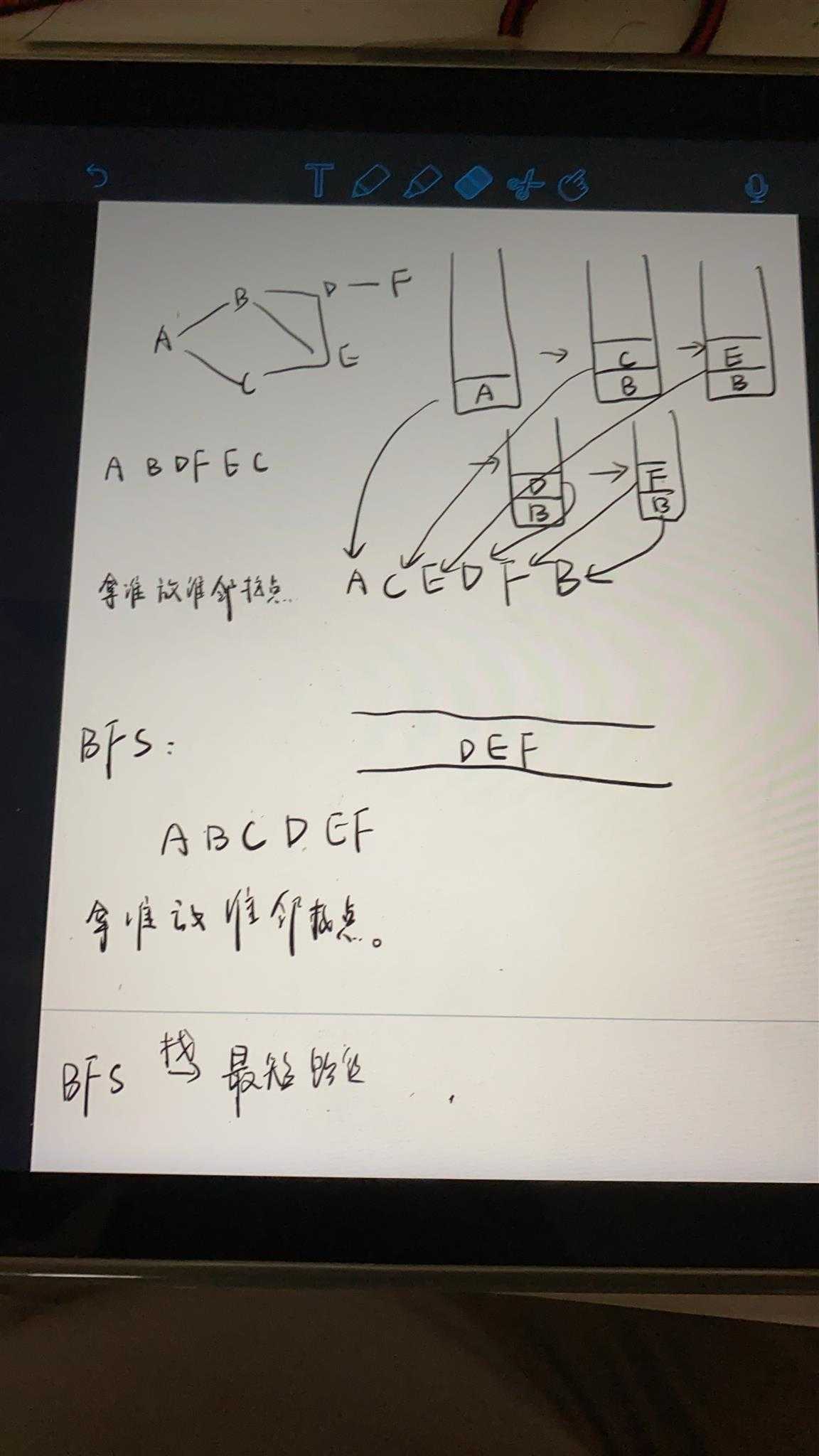
若当前有一个图,从某一点出发,例如上图A点出发,将A点放入队列中,并将A点的邻接点BC放入队列中,而后A出队,而后将B出队,将B的邻接点DE入队,而后C出队,将C的邻接点入队,此时E已经入队则不需要重复,
接下来D出队,邻接点EF入队,E已经存在,无需再入,再E出队,放入E邻接点,最后F出队,发现F出队后队空,即结束遍历,按照上述过程,遍历结果为ABCDEF.
DFS:深度优先遍历。
DFS需要依靠栈来进行操作,依旧按照上图进行操作,假设从A出发,A入栈,而后A出栈,将A的邻接点入栈,BC入栈,C在栈顶,C出栈,其邻接点E入栈,E在栈顶,E出栈,其邻接点D入栈,D在栈顶,D出栈,其邻接点F入栈,
F无邻接点,继续出栈栈顶元素直到栈空,所得序列为ACEDFB.
在通常求最短路径可以借助BFS,如下图(该图转载B站ID:正月点灯笼投稿视频,侵权联删)
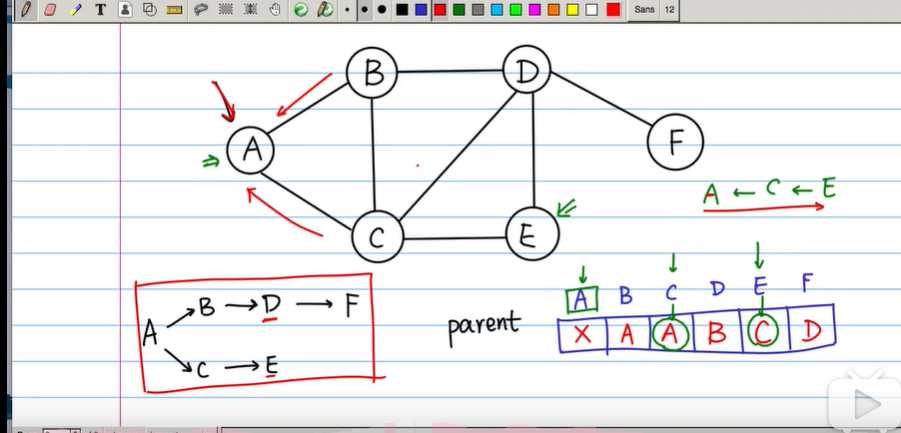
A的BFS类似层次遍历,可以形成如左下角的树(依照邻接关系可得),由图可知A到所有点的最短路径即使该树上的路,所以可以若要求A到E的最短路径,可以从E点逆推,如何逆推?则需要保存每一个点的前一个点是什么,
如A的前一个为空则none,B的前一个为A,C前一个也为A,以此类推,得到所有的父节点,而后从E逆推时,E前一个节点为C,找到C,C前一个为A,则完成,所有ACE是最短路径,在代码实现时,可以考虑一个map进行映射的保存,如p[E]=A。
总结BFS和DFS就是拿走什么的同时即放入什么的邻接点即可。
例题:
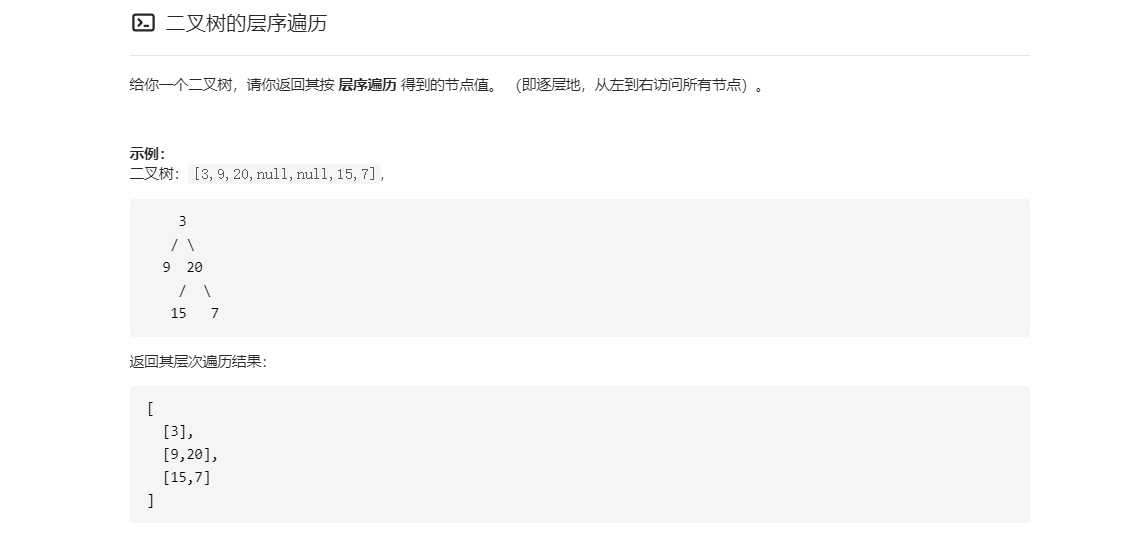
vector<vector<int>>b; if(root==NULL){ return b; }//b作为二维vector保存结果,使得输入如题目要求 queue<TreeNode*> qu; TreeNode* cur=root; qu.push(root);//放入二叉树的根节点 int len = 1;//初始情况下长度为1 TreeNode*t; vector<int>a;//一维vector,保存每一层。 while(!qu.empty()){//队列不为空的情况下进行 for(int i=0;i<len;i++){//对队列中每一个元素都进行如下的操作 t=qu.front();//取得队列的最前一个 a.push_back(t->val);//放入a中 qu.pop();//将第一个出队 if(t->left){ qu.push(t->left); }//若左子树存在则存入队列,左子树即是邻接点 if(t->right){ qu.push(t->right); }//类左子树 } b.push_back(a);//将a放入二维vector中 a.clear();//清空a的元素 len=qu.size();//重新设定队列的长度 } return b;//队列为空的时候,说明遍历完成,可以返回二维vector
原文:https://www.cnblogs.com/OYNanaHlb/p/13580326.html