平衡二叉查找树(Self-balancing binary search tree)又被称为AVL树(有别于AVL算法),且具有以下性质:它是一 棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。
对节点10来说,左边节点10的高度差为1,右边10的高度差为2,所以右边的不是平衡二叉查找树。
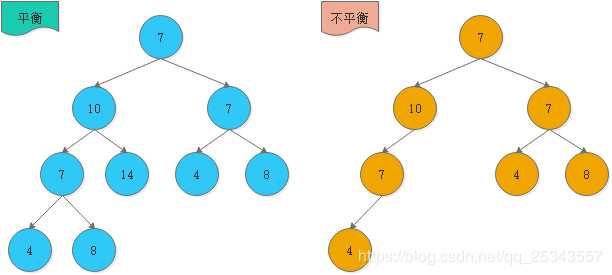
某结点的左子树与右子树的高度(深度)差即为该结点的平衡因子(BF,Balance Factor)。平衡二叉树上所有结点的平衡因子只可能是 -1,0 或 1。如果某一结点的平衡因子绝对值大于1则说明此树不是平衡二叉树。
按照公式 平衡因子 = 左子树的高度 - 右子树的高度
1 : 表示左子树比右子树高
-1 : 表示右子树比左子树高
0 : 表示左子树和右子树等高
上述右图节点10的平衡因子 = 左子树的高度 - 右子树的高度 = 2 - 0 = 2;不满足平衡二叉树的特性。
自平衡的查找树通过定义一些性质,将任意节点的左右子树高度差控制在规定范围内,以达到平衡状态。以红黑树为例,红黑树通过如下的性质定义实现自平衡:
正是红黑树的这5条性质,使一棵n个节点的红黑树始终保持了logn的高度,从而也就解释了上面所说的“红黑树的查找、插入、删除的时间复杂度最坏为O(log n)”这一结论成立的原因。
(注:上述第3、5点性质中所说的叶子节点(NIL节点),包括wikipedia.算法导论上所认为的叶子节点即为树尾端的NIL指针,或者说NULL节点。然百度百科以及网上一些其它博文直接说的叶节点,则易引起误会,因此叶节点非子节点)
如下图所示,即是一颗红黑树(下图引自wikipedia:http://t.cn/hgvH1l):
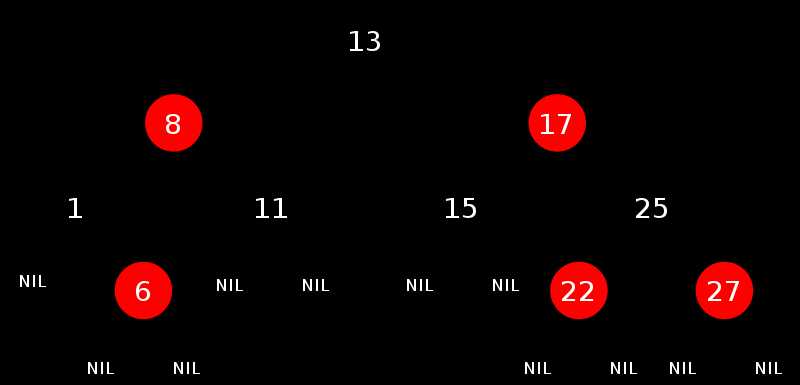
如上图所示,叶子节点(NIL节点)它不包含数据而只充当树在此结束的指示,这些节点在绘图中经常被省略,望看到此文后的读者朋友注意。
在对红黑树进行插入和删除等操作时,对树做了修改可能会破坏红黑树的性质。为了继续保持红黑树的性质,可以通过对节点进行重新着色,以及对树进行相关的旋转操作,即通过修改树中某些节点的颜色及指针结构,来达到对红黑树进行插入或删除节点等操作后继续保持它的性质或平衡的目的。
LL的意思是向左子树(L)的左孩子(L)中插入新节点后导致不平衡,这种情况下需要右旋操作,而不是说LL的意思是右旋,后面的也是一样。如图,节点4插入到节点10的左子树的左子树中,导致节点10的平衡因子 = 2 - 0 = 2,不满足平衡二叉树的特性,需要进行右旋。
我们将这种情况抽象出来,得到下图: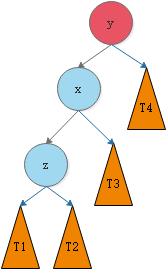
我们需要对节点y进行平衡的维护。步骤如下图所示: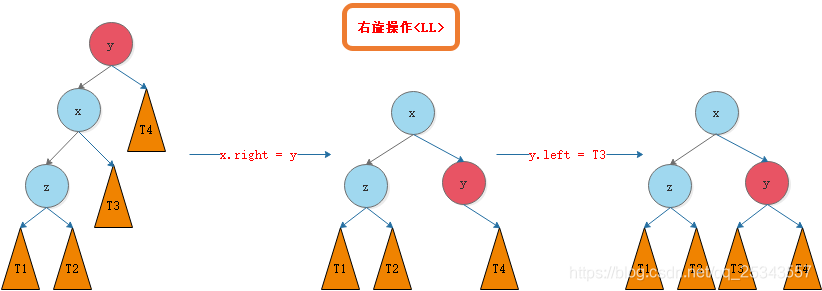
RR的意思是向右子树(R)的左孩子(R)中插入新节点后导致不平衡,这种情况下需要左旋操作,而不是说RR的意思是左旋。如图,节点13插入到节点10的右子树的右子树中,导致节点10的平衡因子 = 0 - 2 = -2,不满足平衡二叉树的特性,需要进行左旋。

我们将这种情况抽象出来,得到下图: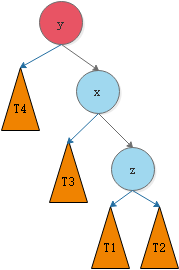
我们需要对节点y进行平衡的维护。步骤如下图所示:

我们将这种情况抽象出来,得到下图: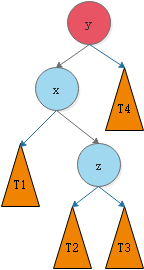
我们需要对节点y进行平衡的维护。步骤如下图所示: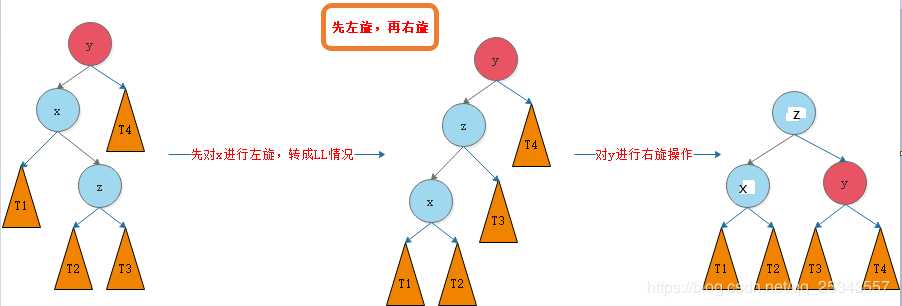

我们将这种情况抽象出来,得到下图:
我们需要对节点y进行平衡的维护。步骤如下图所示: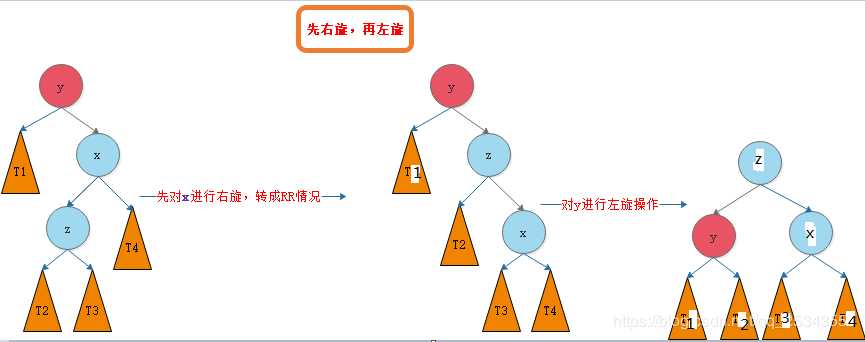
红黑树的插入过程和二叉查找树插入过程基本类似,不同的地方在于,红黑树插入新节点后,需要进行调整,以满足红黑树的性质。性质1规定红黑树节点的颜色要么是红色要么是黑色,那么在插入新节点时,这个节点应该是红色还是黑色呢?答案是红色,原因也不难理解。如果插入的节点是黑色,那么这个节点所在路径比其他路径多出一个黑色节点,这个调整起来会比较麻烦(参考红黑树的删除操作,就知道为啥多一个或少一个黑色节点时,调整起来这么麻烦了)。如果插入的节点是红色,此时所有路径上的黑色节点数量不变,仅可能会出现两个连续的红色节点的情况。这种情况下,通过变色和旋转进行调整即可,比之前的简单多了。
插入的新节点 N 是红黑树的根节点,这种情况下,我们把节点 N 的颜色由红色变为黑色,性质2(根是黑色)被满足。同时 N 被染成黑色后,红黑树所有路径上的黑色节点数量增加一个,性质5(从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点)仍然被满足。
N 的父节点是黑色,这种情况下,性质4(每个红色节点必须有两个黑色的子节点)和性质5没有受到影响,不需要调整。
N 的父节点是红色(节点 P 为红色,其父节点必然为黑色),叔叔节点 U 也是红色。由于 P 和 N 均为红色,所有性质4被打破,此时需要进行调整。这种情况下,先将 P 和 U 的颜色染成黑色,再将 G 的颜色染成红色。此时经过 G 的路径上的黑色节点数量不变,性质5仍然满足。但需要注意的是 G 被染成红色后,可能会和它的父节点形成连续的红色节点,此时需要递归向上调整。
N 的父节点为红色,叔叔节点为黑色。节点 N 是 P 的右孩子,且节点 P 是 G 的左孩子。此时先对节点 P 进行左旋,调整 N 与 P 的位置。接下来按照情况五进行处理,以恢复性质4。
这里需要特别说明一下,上图中的节点 N 并非是新插入的节点。当 P 为红色时,P 有两个孩子节点,且孩子节点均为黑色,这样从 G 出发到各叶子节点路径上的黑色节点数量才能保持一致。既然 P 已经有两个孩子了,所以 N 不是新插入的节点。情况四是由以 N 为根节点的子树中插入了新节点,经过调整后,导致 N 被变为红色,进而导致了情况四的出现。考虑下面这种情况(PR 节点就是上图的 N 节点):
如上图,插入节点 N 并按情况三处理。此时 PR 被染成了红色,与 P 节点形成了连续的红色节点,这个时候就需按情况四再次进行调整。
N 的父节点为红色,叔叔节点为黑色。N 是 P 的左孩子,且节点 P 是 G 的左孩子。此时对 G 进行右旋,调整 P 和 G 的位置,并互换颜色。经过这样的调整后,性质4被恢复,同时也未破坏性质5。
上面五种情况中,情况一和情况二比较简单,情况三、四、五稍复杂。但如果细心观察,会发现这三种情况的区别在于叔叔节点的颜色,如果叔叔节点为红色,直接变色即可。如果叔叔节点为黑色,则需要选选择,再交换颜色。当把这三种情况的图画在一起就区别就比较容易观察了,如下图:
hashMap中链表转为红黑树的两大条件
table数组的大小>64
链表中的元素的数量>8
造一些数据来观察链表转成红黑树的过程
public class Main { public static void main(String[] args) throws NoSuchFieldException, IllegalAccessException { Map<String,String> map = new HashMap<String, String>(); for (int i = 0; i < 65; i++) { map.put("sdf"+ String.valueOf(i),"s" + String.valueOf(i)); if(getHashCodeIndex("sdf"+ String.valueOf(i)) == 26){ System.out.println("index=======26时的key:" + "sdf"+ String.valueOf(i)); } } System.out.println(getHashCodeIndex("caocao")); System.out.println(getHashCodeIndex("sevennnn")); System.out.println(getHashCodeIndex("hate")); System.out.println(getHashCodeIndex("happyy")); System.out.println(getHashCodeIndex("hapqw")); System.out.println(getHashCodeIndex("mg")); System.out.println(getHashCodeIndex("vqv")); System.out.println(getHashCodeIndex("vaf")); System.out.println(getHashCodeIndex("vbde")); System.out.println("================"); map.put("caocao","11"); map.put("sevennnn","22"); map.put("hate","33"); map.put("happyy","44"); map.put("hapqw","55"); map.put("mg","66"); map.put("vqv","77"); map.put("vaf","88"); map.put("vbde","99"); } /** * @Description table大小为128,添加元素时在数组中的下标index * @Param [key] * @return int * @date 2020/8/28 14:32 * @auther Administrator */ public static int getHashCodeIndex(String key){ int h; h = key.hashCode(); int hash = h ^ (h >>> 16); return 127 & hash; } }
输出:
index=======26时的key:sdf15 index=======26时的key:sdf59 26 26 26 26 26 26 26 26 26 ================
所以,当map添加("vqv","77")时,链表中的元素将转化成红黑树
/** * Replaces all linked nodes in bin at index for given hash unless * table is too small, in which case resizes instead. */ final void treeifyBin(Node<K,V>[] tab, int hash) { int n, index; Node<K,V> e; if (tab == null || (n = tab.length) < MIN_TREEIFY_CAPACITY) resize(); else if ((e = tab[index = (n - 1) & hash]) != null) { TreeNode<K,V> hd = null, tl = null; do { TreeNode<K,V> p = replacementTreeNode(e, null); if (tl == null) hd = p; else { p.prev = tl; tl.next = p; } tl = p; } while ((e = e.next) != null); if ((tab[index] = hd) != null) hd.treeify(tab); } }
treeifyBin(Node<K,V>[] tab, int hash)方法是将单向链表(Node)转化成双向链表(TreeNode)

TreeNode类的继承关系、属性等,所以treeNode中是含有next属性的。上述treeNode对象的parent,left,right属性都是null
/** * Entry for Tree bins. Extends LinkedHashMap.Entry (which in turn * extends Node) so can be used as extension of either regular or * linked node. */ static final class TreeNode<K,V> extends LinkedHashMap.Entry<K,V> { TreeNode<K,V> parent; // red-black tree links TreeNode<K,V> left; TreeNode<K,V> right; TreeNode<K,V> prev; // needed to unlink next upon deletion boolean red; TreeNode(int hash, K key, V val, Node<K,V> next) { super(hash, key, val, next); } }
/** * HashMap.Node subclass for normal LinkedHashMap entries. */ static class Entry<K,V> extends HashMap.Node<K,V> { Entry<K,V> before, after; Entry(int hash, K key, V value, Node<K,V> next) { super(hash, key, value, next); } }
static class Node<K,V> implements Map.Entry<K,V> { final int hash; final K key; V value; Node<K,V> next; }
然后treeify(Node<K,V>[] tab)方法形成具体的红黑树,每插入一个节点图示说明红黑树的变化
插入第一个节点("sdf15","s15"),该节点是红黑树的根节点,插入情况的第一种

插入第二个节点("sdf59","s59"),插入情况的第二种
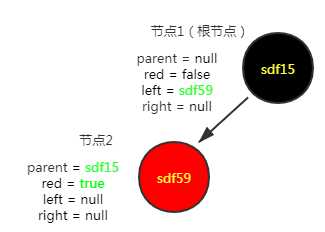
插入第三个节点("caocao","11"),插入情况的第五种
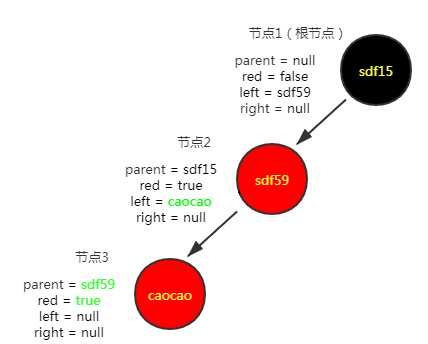
因为新插入的节点是红色,这样节点2和节点3都是红色,不符合红黑树特性,需要进行调整。首先将节点2改为黑色,节点1改为红色。此时节点1的平衡因子为2,不满足平衡二叉树的特性,且根节点为红色不满足红黑树特性,以节点1进行右旋
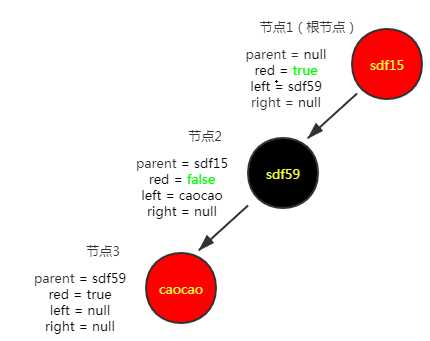
右旋过后的红黑树
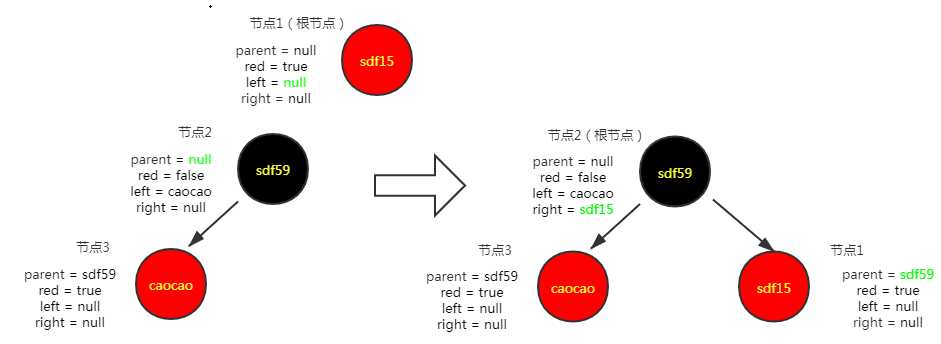
插入第四个节点("sevennnn","22"),插入情况的第三种
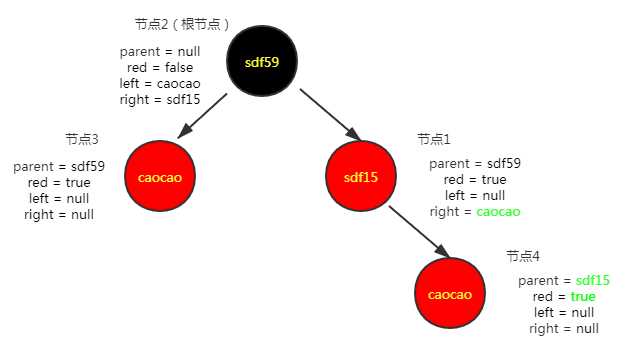
连续两个红色节点不满足红黑树特性,进行维护
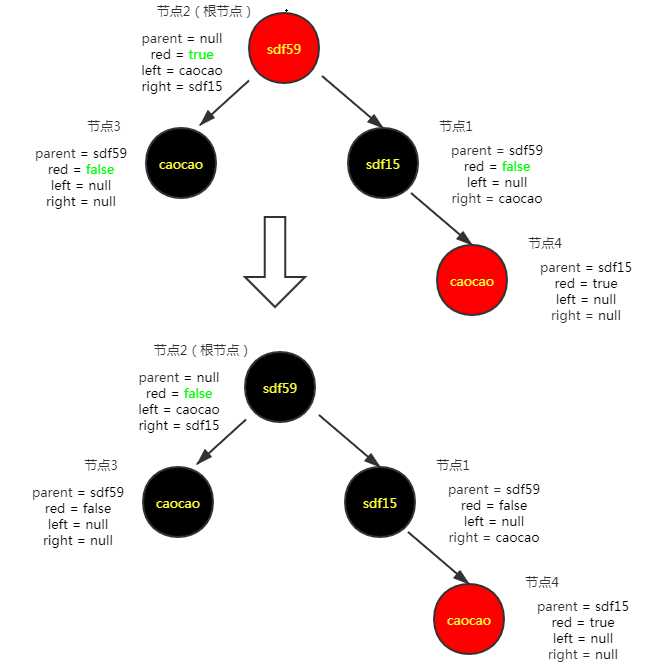
插入第五个节点("hate","33")
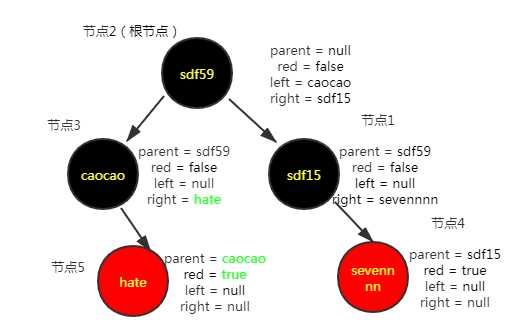
插入第六个节点("happyy","44")
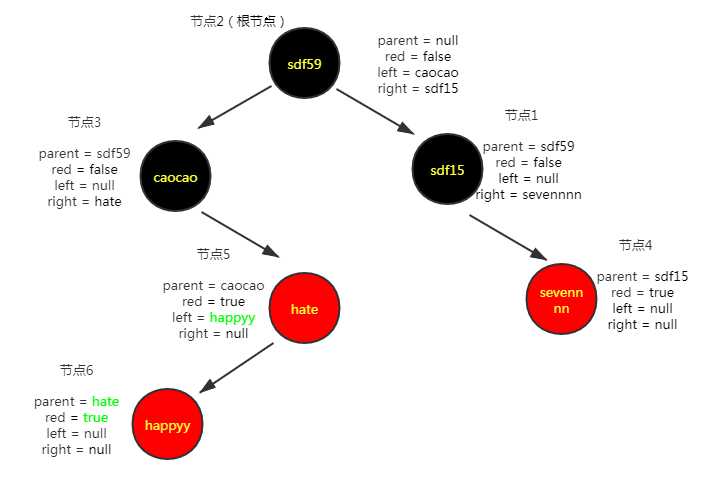
进行右旋
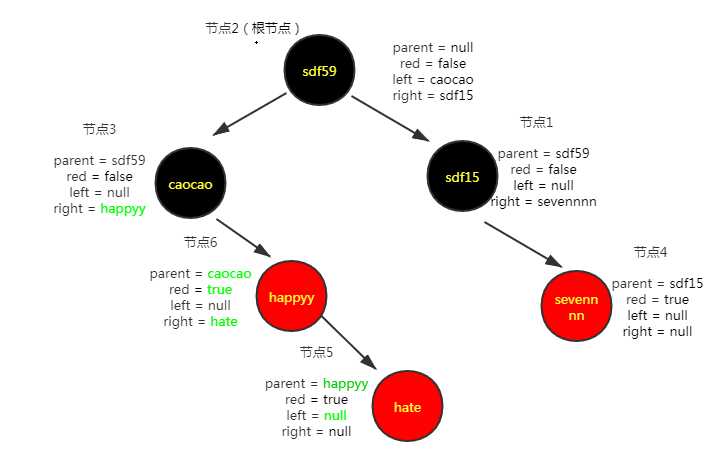
然后是左旋之前
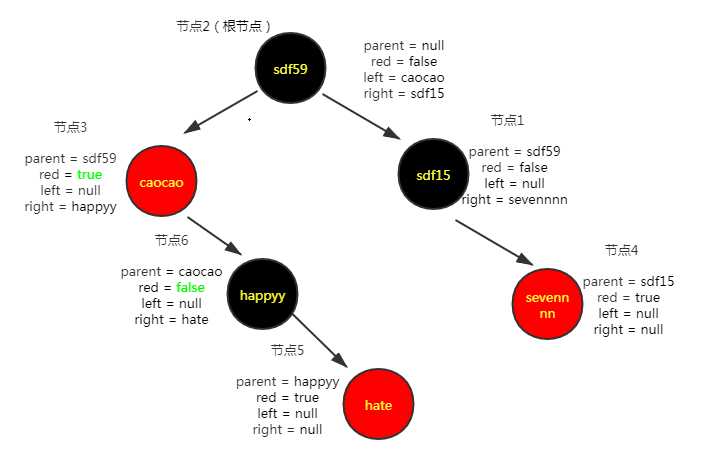
进行左旋
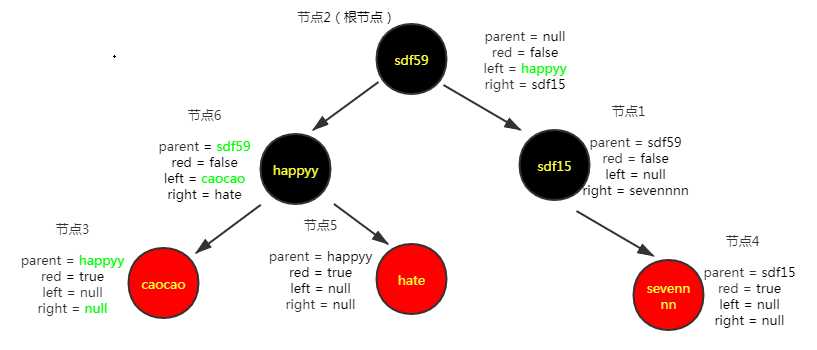
插入第七个节点("hapqw","55")
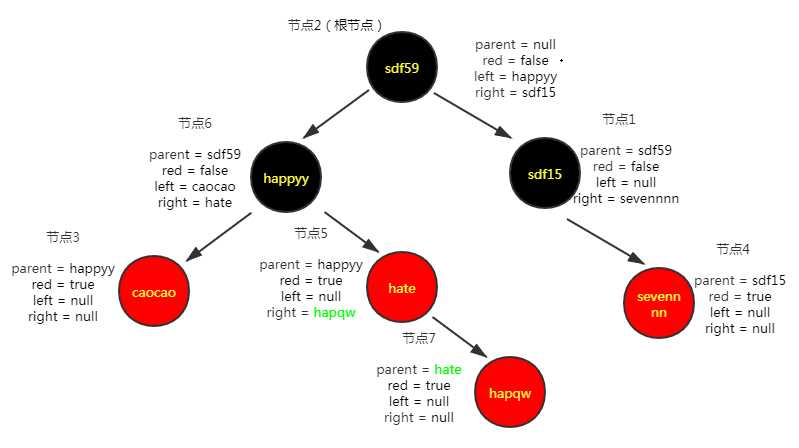
插入节点之后红黑树的维护
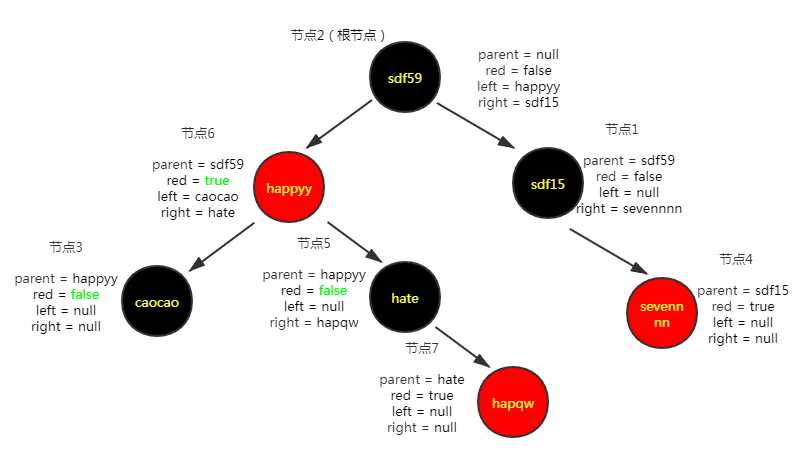
插入第八个节点("mg","66")
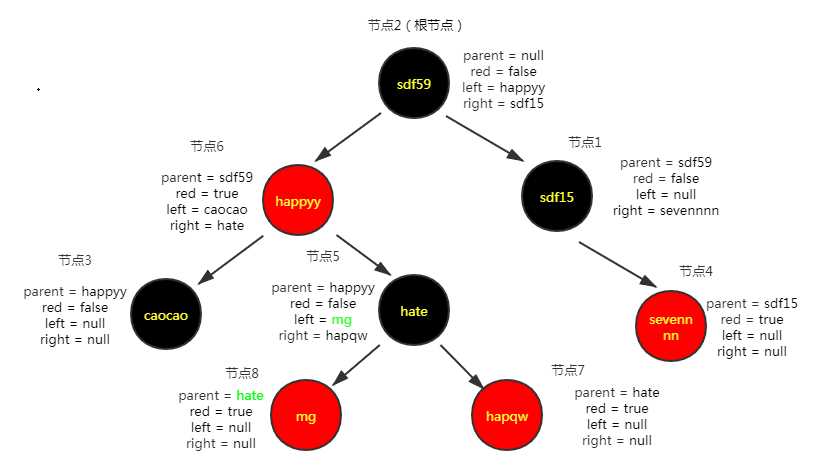
插入第九个节点("vqv","77")
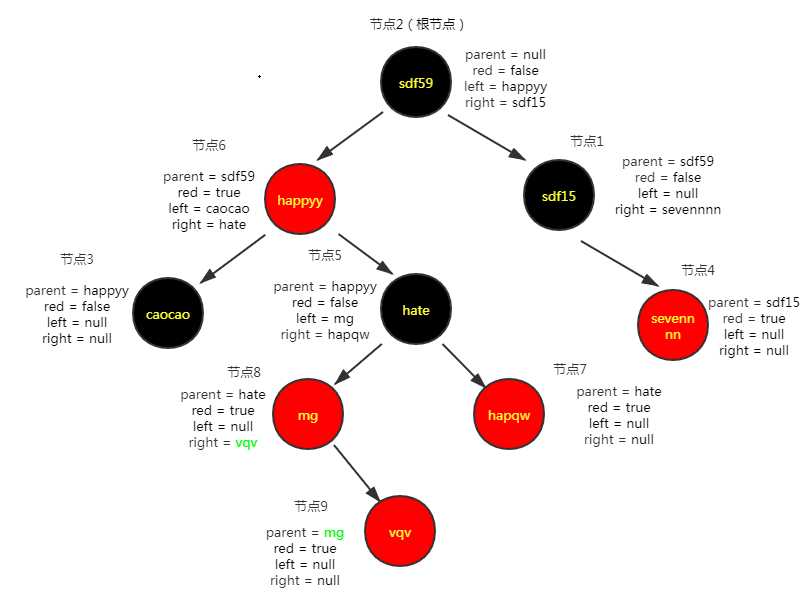
插入节点后进行红黑树的维护
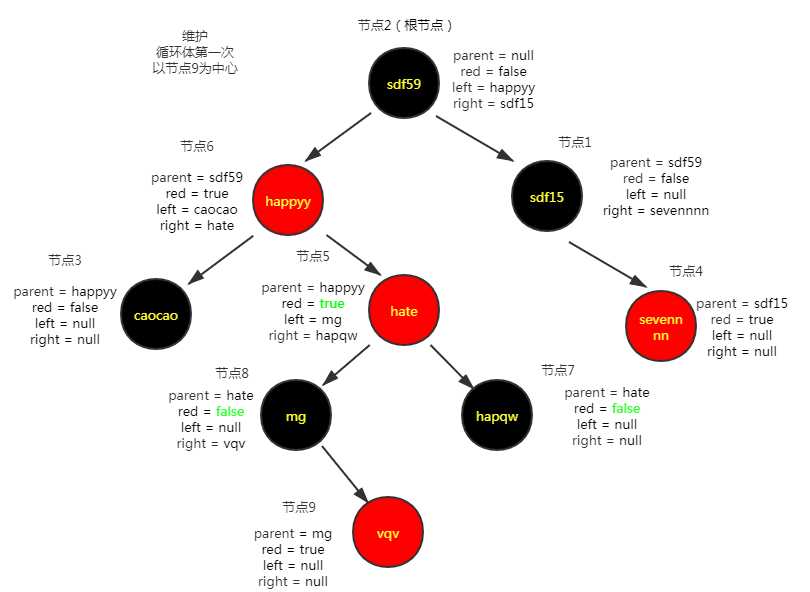
参考:
AVL树平衡因子详解(左子树-右子树)
原文:https://www.cnblogs.com/zfyang2429/p/13577767.html