AtCoder Beginner Contest 177 D - Friends (并查集)

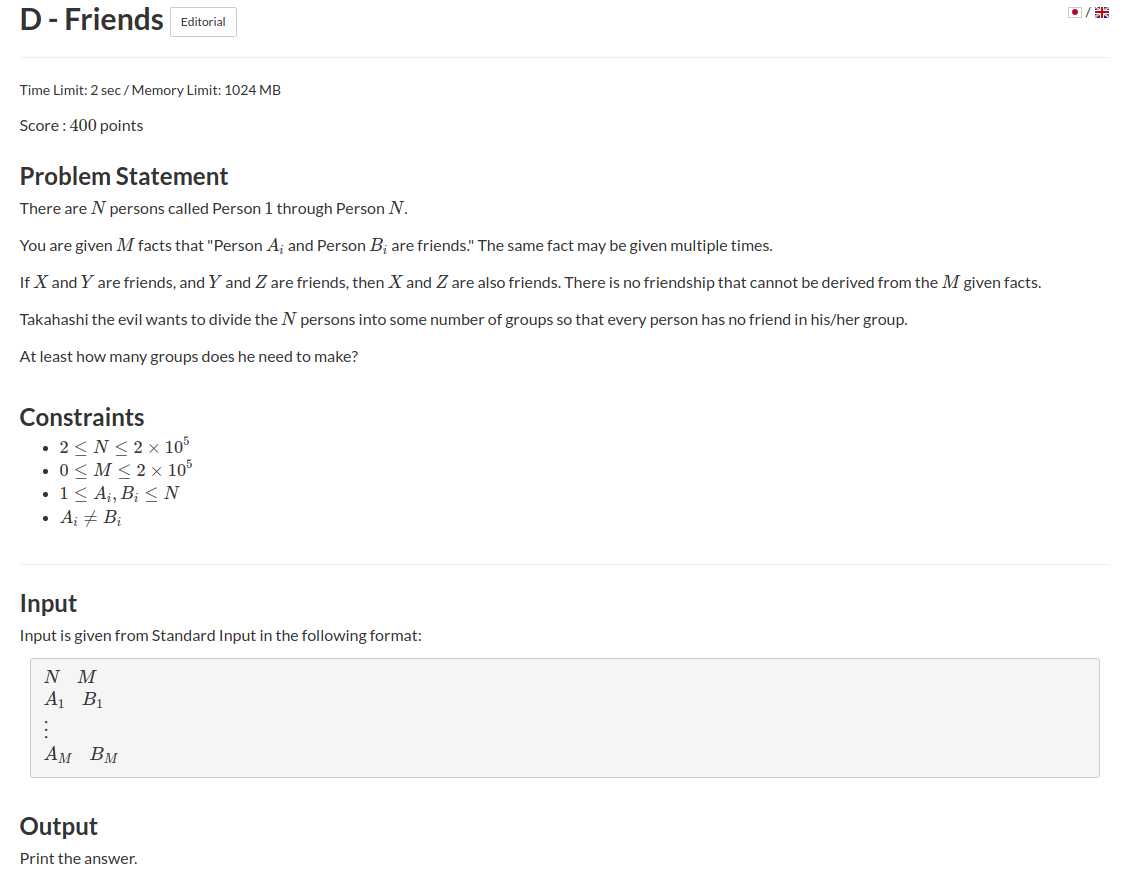
• 题意:有\(n\)个人,给你\(m\)对朋友关系,朋友的朋友也是朋友,现在你想要将他们拆散放到不同的集合中,且每个集合中的人没有任何一对朋友关系,问最少需要多少集合.

• 题解:首先用并查集将朋友关系维护到集合中,然后贪心,其实我们所需要的集合数就是之前并查集维护的集合中的最大元素个数.

• 代码:

  int n,m;
  int u,v;
  int p[N];
  map<int,int> mp;
  
  int find(int x){
  	if(p[x]!=x) p[x]=find(p[x]);
  	return p[x];
  }
  
  int main() {
      //ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
  	n=read();
  	m=read();
  	for(int i=1;i<=n;++i) p[i]=i;
  	for(int i=1;i<=m;++i){
  		u=read();
  		v=read();
  		p[find(u)]=find(v);
  	}
  
  	for(int i=1;i<=n;++i){
  		mp[find(i)]++;
  	}
  
  	int res=0;
  	for(auto w:mp){
  		res=max(res,w.se);
  	}
  
  	printf("%d\n",res);
  
      return 0;
  }
  

AtCoder Beginner Contest 177 D - Friends (并查集)

原文：https://www.cnblogs.com/lr599909928/p/13600141.html