损失函数

一、损失函数和代价函数、目标函数的区别和练习

在机器学习中，经常会碰到 Loss Function、Cost Function 和 Objective Function，这三个术语，我们要了解他们之间的区别和联系。

（1）损失函数（Loss Function）通常是针对单个训练样本而言，给定一个模型输出 y^‘  （预测值）和一个真实的y，损失函数输出一个实值 

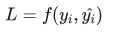
（2）代价函数（Cost Function）通常是针对整个训练集的总损失

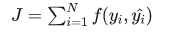
（3）目标函数（Objective Function）表示任意希望被优化的函数，用于机器学习领域和非机器学习领域

 一句话总结三者的关系就是：A loss function is a part of a cost function which is a type of an objective function。

二、损失函数的类别

通常机器学习每一个算法中都会有一个目标函数，算法的求解过程是通过对这个目标函数优化的过程。在分类或者回归问题中，通常使用损失函数（代价函数）作为其目标函数。损失函数用来评价模型的预测值和真实值不一样的程度，损失函数越好，通常模型的性能越好。不同的算法使用的损失函数不一样。

损失函数分为经验风险损失函数和结构风险损失函数。经验风险损失函数指预测结果和实际结果的差别，结构风险损失函数是指经验风险损失函数加上正则项。通常表示为如下：

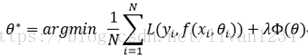其中，前面的均值项表示经验风险函数，L表示损失函数，后面的是正则化项（regularizer）或惩罚项（penalty term），它可以是L1、L2或者其他正则函数。整个式子表示要找到使得目标函数最小的值

（1）均方差（Mean Squared Error (MSE）损失（Mean Squared Error Loss）是机器学习、深度学习回归任务中最常用的一种损失函数，也称为 L2 Loss。其基本形式如下

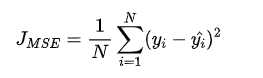
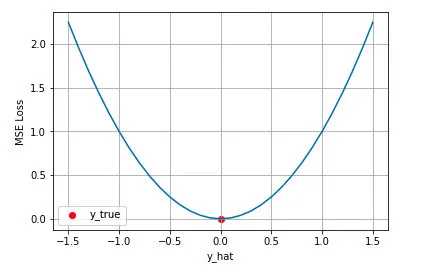
从直觉上理解均方差损失，这个损失函数的最小值为 0（当预测等于真实值时），最大值为无穷大。下图是对于真实值 y=0  ，不同的预测值 [-1.5,1.5]  的均方差损失的变化图。横轴是不同的预测值，纵轴是均方差损失，可以看到随着预测与真实值绝对误差 的增加，均方差损失呈二次方地增加。

实际上在一定的假设下，我们可以使用最大化似然得到均方差损失的形式。假设模型预测与真实值之间的误差服从标准正态分布(高斯分布)（ μ=0，σ=1 ），则给定一个 x_i  , 模型输出真实值y_i   的概率为

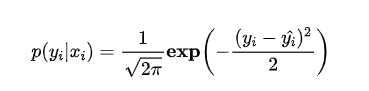
进一步我们假设数据集中 N 个样本点之间相互独立，则给定所有  输出所有真实值  的概率，即似然 Likelihood，为所有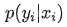的累乘，

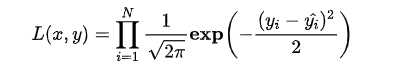
通常为了计算方便，我们通常最大化对数似然 Log-Likelihood，

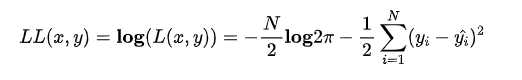
去掉与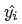无关的第一项，然后转化为最小化负对数似然 Negative Log-Likelihood

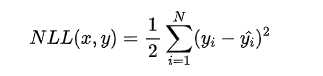
可以看到这个实际上就是均方差损失的形式。也就是说在模型输出与真实值的误差服从（正态分布）高斯分布的假设下，最小化均方差损失函数与极大似然估计本质上是一致的，因此在这个假设能被满足的场景中（比如回归），均方差损失是一个很好的损失函数选择；当这个假设没能被满足的场景中（比如分类），均方差损失不是一个好的选择 

 （2）平均绝对误差（Mean Absolute Error Loss）

基本形式和原理：

损失函数

原文：https://www.cnblogs.com/cgmcoding/p/13606876.html