前面一篇文章我们讲了栈,现在来讲另一个构思算法的辅助工具--队列。它的访问规则与栈相反,采取先进先出的规则
队列(queue)是一种抽象的数据结构(ADT),它也可以用其他的数据结构来实现,比如说前面讲过的数组。
它是一种受限访问的数据结构,遵循先进后先(FIFO)的规则,即最先进入队列的最先出来的原则。
就像排队一样,最先到的最先买票,最后到的,排到队伍的最后
队列分为:
①单向队列:限制在一端插入数据(队尾),一端删除数据(队头)
②双向队列:两端都可以插入和删除数据
③优先队列:维护好队列数据的顺序,使队列数据呈从大到小或从小到大的顺序
在写代码之前,我们需要知道队列的实现与栈有点稍微的不同。
正常的想法是,队列删除了队头元素,将后面的元素往前移动一位,就像排队一样,不断向前移动
但实际上,看过之前排序的朋友应该知道,数据移动是比较麻烦的,尤其是队列数据较多的时候,效率很低
我们选择的做法是移动队头和队尾,如下图:
在队头或队尾到头的时候,将其移动到另一端。循环利用:
Java实现代码:
/** * 队列 */ public class MyQueue { private Object[] array; private int maxSize;//最大容量 private int head;//队头 private int tail;//队尾 private int nItem;//实际元素数 public MyQueue(int size){ maxSize = size; array = new Object[size]; head = 0; tail = -1; nItem = 0; } /** * 插入 * @param obj */ public void insert(Object obj){ //判断是否超过最大容量 if(!isFull()){ //到头时,将尾部移到队列开头 if(tail == maxSize-1)tail=-1; array[++tail] = obj; nItem++; } } /** * 删除 * @return */ public Object remove(){ Object removeValue = null; //判断队列是否为空 if(!isEmpty()){ Object headValue = array[head]; array[head] = null;//gc if(head == maxSize-1) head=0; else head++; removeValue = headValue; nItem--; } return removeValue; } /** * 查看队头元素 * @return */ public Object peekHead(){ return array[head]; } /** * 查看队尾元素 * @return */ public Object peekTail(){ return array[tail]; } public boolean isFull(){ return nItem == maxSize; } public boolean isEmpty(){ return nItem == 0; }
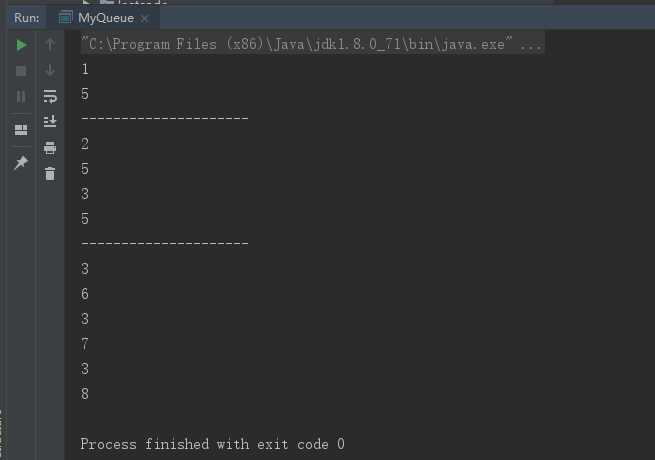
我们来测试以下:
public static void main(String[] args) { MyQueue queue = new MyQueue(5); queue.insert(1); queue.insert(2); queue.insert(3); queue.insert(4); queue.insert(5); System.out.println(queue.peekHead()); System.out.println(queue.peekTail());//[1,2,3,4,5] System.out.println("---------------------"); queue.remove(); System.out.println(queue.peekHead()); System.out.println(queue.peekTail());//[null,2,3,4,5] queue.remove(); System.out.println(queue.peekHead()); System.out.println(queue.peekTail());//[null,null,3,4,5] System.out.println("---------------------"); queue.insert(6); System.out.println(queue.peekHead()); System.out.println(queue.peekTail());//[6,null,3,4,5] queue.insert(7); System.out.println(queue.peekHead()); System.out.println(queue.peekTail());//[6,7,3,4,5] queue.insert(8); System.out.println(queue.peekHead()); System.out.println(queue.peekTail());//满了[6,7,3,4,5] }
测试结果:
双端就是队头和队尾都可以进行操作的队列,也可以通过限制操作来实现单向队列和栈。
我们来讲下优先队列,优先级队列(priority queue)是比栈和队列更专用的数据结构,在优先级队列中,数据项按照关键字进行排序,
关键字最小(或者最大)的数据项往往在队列的最前面,而数据项在插入的时候都会插入到合适的位置以确保队列的有序。
我们也可以通过数组来实现,不过实际优先队列通过堆来实现,可参考public class PriorityQueue<E> extends AbstractQueue<E>
代码实现:
/** * 优先队列 */ public class MyPriorityQueue { private int[] array;//使用int[]便于比较 private int maxSize;//最大容量 private int nItem;//实际元素数 public MyPriorityQueue(int size){ maxSize = size; array = new int[size]; nItem = 0; } /** * 插入 */ public void insert(int s){ if(!isFull()){ if(nItem == 0){ array[nItem++] = s; }else{ int j = nItem - 1; //使用插入排序,从小到大排序 while(j >= 0 && array[j] > s){ array[j+1] = array[j]; j--; } array[j+1] = s; nItem++; } } } /** * 删除 */ public int remove(){ int removeValue = -1;//置为-1表示没有 //判断队列是否为空 if(!isEmpty()){ int k = nItem - 1; removeValue = array[k]; array[k] = -1; nItem--; } return removeValue; }
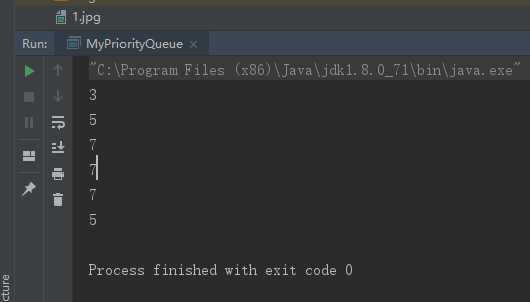
//获取最大值 public int peek(){ return array[nItem-1]; } public boolean isFull(){ return nItem == maxSize; } public boolean isEmpty(){ return nItem == 0; } public static void main(String[] args) { MyPriorityQueue queue = new MyPriorityQueue(5); queue.insert(3); System.out.println(queue.peek());//[3,0,0,0,0] queue.insert(5); System.out.println(queue.peek());//[3,5,0,0,0] queue.insert(7); System.out.println(queue.peek());//[3,5,7,0,0] queue.insert(2); System.out.println(queue.peek());//[2,3,5,7,0] queue.insert(1); System.out.println(queue.peek());//[1,2,3,5,7] queue.remove(); System.out.println(queue.peek());//[1,2,3,5,-1] } }
测试结果:
这里作简单处理,只有用比大小的方式模拟优先队列,可以优化直接传入Comparable作自定义的优先级比较
作为一个有序的集合,优先队列可以实现许多功能,比如数据排序,取最大,最小值等
插入数据时需要一一比较数据大小,时间复杂度为O(N),可以用堆来改进插入操作
①队列只允许访问第一个插入的数据项
②队列的重要操作是在队头删除数据,队尾添加数据
③队列可以实现成循环队列,将数据下标从末端移回开始位置
④优先队列可以访问最小或最大数据
⑤优先队列的重要操作是插入时比较数据的优先级,将数据插到正确优先级的位置
原文:https://www.cnblogs.com/ccxin/p/13617763.html