一、什么是堆?
堆是一种数据结构,是一种特殊的二叉树。堆安排在一个连续的数组中,这个数组的下标从 1 开始,节点 i 的子节点下标可以用 i * 2, i * 2 + 1 计算得到。
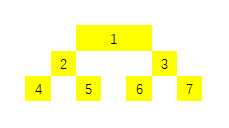
例如,3 的子节点就是 3 * 2 = 6, 3 * 2 + 1 = 7。
此外,节点直接还满足这样一个性质:父节点总是【大于/小于】它的两个子节点。父节点较大的称为大根堆,反之为小根堆。子节点之间没有大小关系的要求。
二、如何建堆?
对于只有一个元素的数组,很显然它不需要任何操作,就是一个堆。
如果一个数组有更多的元素,我们可以试图想想:如果二叉树根节点的左子树和右子树都是一个合法的堆,我们要如何调整根节点,使整个数组变为一个堆?
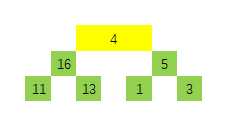
以大根堆为例,现在两边的子树都是一个合法的大根堆了,如何调整 4 的位置呢?答案是让 4 下沉,并让数值最大的子节点上浮。
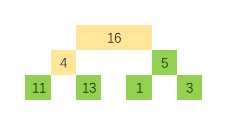
但是这样的话,左边这个堆的性质又被破坏了。我们如法炮制,继续让 4 下沉。
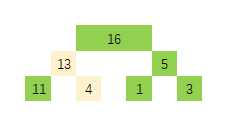
这样,我们就得到了一个合法的堆。
现在的问题就是如何把这个下沉操作应用到整个数组,使其成为堆。
解决方法如下:
1. 对于叶子节点,显然它是一个合法的堆。

2. 我们从最后一个非叶节点开始,对这些节点进行下沉操作。这相当于在包含非叶节点的倒数第一层开始。
3. 由于是包含非叶节点的倒数第一层,我们可以确保我们操作的节点全部具备了左右子树均为合法堆的性质。

4. 接着我们会前往包含非叶节点的倒数第二层。当我们在这一层的时候,底下的这一层已经全部是调整好的节点了。因此,我们可以逐个对它们进行下沉。

5. 这样子,我们就能得到一个完全的堆。
void heapify(vector<int> &a, int index) { // leftindex = (index + 1) * 2 - 1 = index * 2 + 1 // rightindex 同理 int leftIndex = index * 2 + 1; int rightIndex = index * 2 + 2; // 如果是叶节点,下沉结束。 // 由堆的性质,只需要检查左节点是否为空。 if (leftIndex >= a.size()) { return; } // 我们确保了 index 是非叶节点, // 因此至多只需要检查右节点是不是空。 if (rightIndex >= a.size()) { if (a[index] < a[leftIndex]) { swap(a[index], a[leftIndex]); heapify(a, leftIndex); } } else { int maxIndex = index; if (a[leftIndex] > a[maxIndex]) { maxIndex = leftIndex; } if (a[rightIndex] > a[maxIndex]) { maxIndex = rightIndex; } if (maxIndex != index) { swap(a[index], a[maxIndex]); heapify(a, maxIndex); } } } void makeheap(vector<int>& a) { int n = a.size(); // 因为数组的下标以 0 开始计,所以 n / 2 还要再 - 1 才是正确的下标。 for (int i = n / 2 - 1; i >= 0; i--) { heapify(a, i); } }
三、如何堆排序
当我们构建了大根堆之后,我们就可以提取堆的根,知道整个数组的最大值。
而取了这个节点之后,谁来当根?当了之后是怎么维护堆的性质的?

考虑到整个堆除了没有根之外,都是合法大根堆根节点,我们只需要把数组的最后一位拿出来放在堆顶。此时我们的堆就变成了“除了根节点,其它的节点都是合法”。
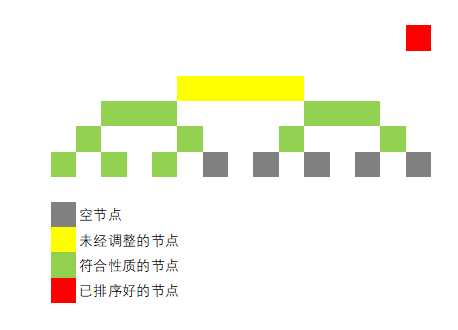
只需要经过提取 -> 调换 -> 维护 -> 提取 -> ... 这样的循环,我们就可以得到一个排序好的数组。

然而这样的话我们会有额外的 O(n) 空间开销,因此比起把提取的根节点放到一个新的数组里,我们不如直接置换到堆的末尾。

这样我们就完成了整个堆排序的算法。
// 注意:为了完成堆排序,heapify 函数额外添加了一个当前堆长度的参数。 void heapify(vector<int> &a, int index, int maxlen) { // leftindex = (index + 1) * 2 - 1 = index * 2 + 1 // rightindex 同理 int leftIndex = index * 2 + 1; int rightIndex = index * 2 + 2; // 如果是叶节点,下沉结束。 // 由堆的性质,只需要检查左节点是否为空。 if (leftIndex >= maxlen) { return; } // 我们确保了 index 是非叶节点, // 因此至多只需要检查右节点是不是空。 if (rightIndex >= maxlen) { if (a[index] < a[leftIndex]) { swap(a[index], a[leftIndex]); heapify(a, leftIndex, maxlen); } } else { int maxIndex = index; if (a[leftIndex] > a[maxIndex]) { maxIndex = leftIndex; } if (a[rightIndex] > a[maxIndex]) { maxIndex = rightIndex; } if (maxIndex != index) { swap(a[index], a[maxIndex]); heapify(a, maxIndex, maxlen); } } } void makeheap(vector<int>& a) { int n = a.size(); // 因为数组的下标以 0 开始计,所以 n / 2 还要再 - 1 才是正确的下标。 for (int i = n / 2 - 1; i >= 0; i--) { heapify(a, i, a.size()); } } void heapsort(vector<int>& heap) { for (int i = heap.size() - 1; i >= 1; i--) { swap(heap[0], heap[i]); heapify(heap, 0, i); } }
原文:https://www.cnblogs.com/KakagouLT/p/13622610.html