老是写不好二分，特此学习总结一下。

lower_bound 和 upper_bound

这两个函数基本上能替代手写的二分查找，但是千万别弄错俩函数的作用。
lower_bound 返回数组中第一个不小于目标值的元素的iterator，（第一个>=target的数）
upper_bound 返回数组中第一个大于目标值的元素的iterator， （第一个>target的数）

手写二分查找

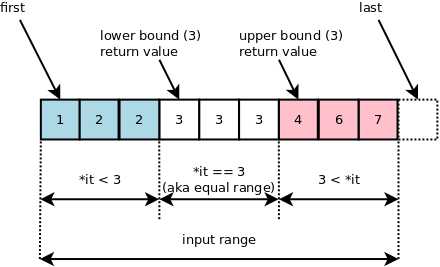
主要是熟练使用二分，不单单只是用来查找一个数 ，而是能指哪打哪，用来解决带有单调性的数组问题，这才是二分的威力。

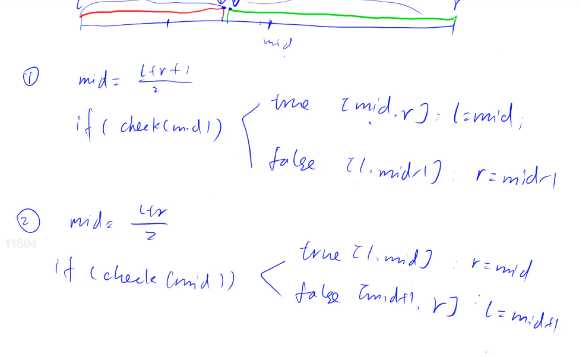
经典二分模板, 一个是区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用， 一个是区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用。当数组为前段false,后端true时候，用（1），前段true，后段false时，用（2）

bool check(int x) {/* ... */} // 检查x是否满足某种性质

// 区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用：
int bsearch_1(int l, int r)
{
    while (l < r)
    {
        int mid = l + r >> 1;
        if (check(mid)) r = mid;    // check()判断mid是否满足性质
        else l = mid + 1;
    }
    return l;
}
// 区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用：
int bsearch_2(int l, int r)
{
    while (l < r)
    {
        int mid = l + r + 1 >> 1;
        if (check(mid)) l = mid;
        else r = mid - 1;
    }
    return l;
}

// 作者：yxc
// 链接：https://www.acwing.com/blog/content/277/
// 来源：AcWing
// 著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

二分查找 ：数的范围

经典题AcWing 789. 数的范围，给定数组，如1 2 2 3 3 4， 和target， 如3，找到3的范围[3,4]。

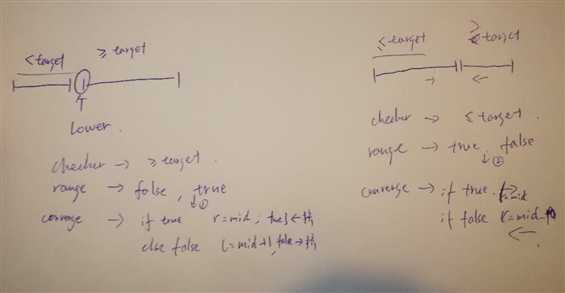
可见，本题需要找到arr[low] <= target的下界，还要找到arr[up] >= target的下界，根据区间是前false后true还是前true后false来使用二分方法。

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

vector<int> arr {};
int n, m, target;


// 两种方法用来找符合checker的最左边以及符合checker的最右边。
int low(int l, int r, int target) {
    while(l<r) {
        int mid = l+r>> 1;
        if (arr[mid]>=target) r = mid;
        else l = mid+1;
    }
    return l;
}

int up(int l, int r, int target) {
    while (l<r) {
        int mid = l+r+1 >> 1;
        if (arr[mid]<=target) l = mid;
        else r = mid-1;
    }
    return r;
}

int main() {
    cin >> n >> m;
    arr.resize(n);
    
    for (int i=0; i<n; i++) cin >> arr[i];
    
    for (int i=0; i<m; i++) {
        cin >> target;
        int lower = low(0, n-1, target);
        int upper = up(lower, n-1, target);
        if (arr[lower]!=target) cout << "-1 -1" << endl;
        else 
        cout << lower<< " " << upper << endl;
    }
}

lower_bound 和 二分

原文：https://www.cnblogs.com/linsinan1995/p/13620590.html