DP这个词,指的是一系列的算法,这些算法主要用来解决:当我有了一个可以完美模拟马尔可夫过程的模型之后,如何计算最优policies的问题。注意是policies,表明最优的策略可能不止一个。经典的DP算法在强化学习中的应用受限的原因有两个:一个是强假设满足不了,就是无法保证我能先有一个完美的模型来描述整个马尔可夫过程;另一个就是计算开销太大。但这仍掩盖不了其理论上的重要性。DP可以帮助我们更好地理解本书余下部分讨论的方法。事实上,这些方法都可以看成是尽可能的获得跟DP一样的效果,只是在强假设条件和计算开销上进行了优化。
从这章开始,我们假设我们面对的环境是有限MDP过程,也就是它的状态集合S和动作集合,都是有限的。其动态特性由一系列的状态转移矩阵给出:
当前reward的期望由下式给出:
尽管DP思想可以用于连续性的状态空间和动作空间,精确解只有在特定情形下才能得到。获得连续空间下的近似解的一种常用方法是把连续空间进行数值化变换,然后使用有限马尔可夫方法。我们第九章讨论的方法可以用于连续空间下的问题。
DP的核心思想,就是使用value function作为依据,指导policies的搜索过程。这一章我们讨论如何使用DP来计算第三章定义的value function。正如我们讨论过的,一旦我们找到了满足bellman 最优方程的最优value functions,我们就能找到最优policies。
回顾一下最优value function的定义:
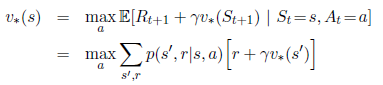
或者:

正如我们将要看到的那样,DP算法做的事情就是把这些bellman functions转变成优化value functions近似值的更新规则。
首先我们来看一下如何计算对应任一policy的value function。这个叫做策略评估。我们也称之为prediction problem。回忆一下第三章,对于所有,
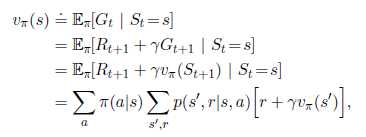
这里表示在policy为
,状态为s的情况下,action为a的概率。这个value function和上一段描述的并没有本质不同,只是多了policy的限制。只要满足
或者在策略
的情况下,所有的从状态s起始的路径都会有终止状态,那么这个valun function就是存在且唯一的。
如果环境的动态转移特性是完全可知的,那么上式其实就是个线性方程,带有
个未知数。在这种情况下,暴力解是可行的,也是是确定的。对于我们来说,迭代的计算方式是最适合的。假设我们有一系列的近似value function:
,每一个都把状态集合S映射到实数集R。最初的近似value function:
,是任意选择的(注意这里的0是指初始的value function,不是指状态的开始。事实上,每个迭代的value function都对所有的状态有个对应的实数映射。这也是为何后面会收敛于真实的
的原因)。然后后面的每一个近似value function都按照上式迭代求解。事实上,随着迭代的进行,最终value function会逐渐收敛于
。这个算法叫做iterative policy evaluation。
参考文献:
https://zhuanlan.zhihu.com/p/27659382
原文:https://www.cnblogs.com/Lee-yl/p/13636572.html