一.算法简介
模拟生物在自然环境中的遗传和进化的过程而形成的自适应全局优化搜索算法;本质是一种并行、高效、全局搜索的方法,能在搜索过程中自动获取和积累有关搜索空间的知识,并自适应地控制搜索过程以求得最优。
在遗传算法的每一代中,根据个体在问题域中的适应度值和从自然遗传学中借鉴来的再造方法进行个体选择,产生一个新的近似解。这个过程导致种群中个体的进化,得到的新个体比原个体更能适应环境,就像自然界中的改造一样。
二.算法理论
2.1 生物学基础
自然选择学说:遗传和变异是决定生物进化的内在因素。遗传:指父代与子代之间,在性状上存在的相似现象;变异:指父代与子代之间,以及子代的个体之间,在性状上存在的差异现象。
通过对环境的选择、基因的交叉和变异这一生物演化的迭代过程的模仿,才提出了能够用于求解最优化问题的强鲁棒性和自适应性的遗传算法。生物遗传和进化的规律有:
①生物的所有遗传信息都包含在其染色体中,染色体决定了生物的性状,染色体是由基因及其有规律的排列所构成的。
②生物的繁殖过程是由其基因的复制过程来完成的。同源染色体的交叉或变异会产生新的物种,使生物呈现新的性状。
③对环境适应能力强的基因或染色体,比适应能力差的基因或染色体有更多的机会遗传到下一代。
2.2 基本概念
遗传算法使用群体搜索技术,将种群代表一组问题解,通过对前种群施加选择、交叉和变异等一系列遗传操作来产生新一代的种群,并逐步使种群进化到包含近似最优解的状态。
| 群体 | 可行解集 |
| 个体 | 可行解 |
| 染色体 | 可行解的编码 |
| 基因 | 可行解编码的分量 |
| 基因形式 | 遗传编码 |
| 适应度 | 评价函数值 |
| 选择 | 选择操作 |
| 交叉 | 交叉操作 |
| 变异 | 变异操作 |
群体和个体:
群体:生物进化过程中的一个集团,表示可行解集
个体:组成群体的单个生物体,表示可行解
染色体和基因:
染色体:包含生物体所有遗传信息的化合物,表示可行解的编码
基因:控制生物体某种性状(即遗传信息)的基本单位,表示可行解编码的分量
遗传编码:
将优化变量转化为基因的组合表示形式,优化变量的编码机制有二进制编码、十进制编码(实数编码)等。
二进制编码和实数编码:
具体编码方法在此不做赘述
对于二进制编码,一般来说,编码精度越高,所得到的解的质量也越高,意味着解更为优良;但同时,由于遗传操作所需的计算量也更大,因此算法耗时更长。
人们在解决一些数值优化问题(尤其是高维、连续优化问题)时,经常采用实数编码方式。优点是计算精确度高,便于和经典连续优化算法结合,适用于数值优化问题;但缺点是适用范围有限,只能用于连续变量问题。
适应度:
生物群体中个体适应生存环境的能力。在遗传算法中,用来评价个体优劣的数学函数,称为个体的适应度函数。
常见的适应度函数构造方法主要有:目标函数映射成适应度函数,基于序的适应度函数等。
遗传操作:
优选强势个体的“选择”、个体间交换基因产生新个体的“交叉”、个体基因信息突变而产生新个体的“变异”这三种交换的统称。
遗传算子:
①选择算子:根据个体的适应度fi,按照一定的规则或方法,从第t代群体P(t)中选择出一些优良的个体遗传到下一代群体P(t+1)中,个体适应度越大,其被选择的机会越大
②交叉算子:将群体P(t)中选中的各个个体随机搭配,对每一对个体,以某一概率(交叉概率Pc)交换它们之间的部分染色体。通过交叉,遗传算法的搜索能力得以飞跃提高
交叉操作一般包括:首先从交配池中随机取出要交配的一对个体;然后根据位串长度L,对要交配的一对个体,随机选取[1,L-1]中的一个或多个整数k作为交叉位置;最后,根据交叉概率Pc实施交叉操作,配对个体在交叉位置处,相互交换各自的部分基因,从而形成新的一对个体。
③变异算子:对群体中的每个个体,以某一概率(变异概率Pm)将某一个或某一些基因座上的基因值改变为其他的等位基因值,包括实值变异、二进制变异。
变异操作一般包括:首先对种群中所有个体按实现设定的变异概率判断是否进行变异;然后对进行变异的个体随机选择变异位进行变异
2.3 标准遗传算法
又称经典遗传算法,优化变量由二进制编码来描述,多个优化变量的二进制编码串接在一起组成染色体,这种编码既适用于变异操作,又适用于交叉操作。在创建初始群体时,代表个体的二进制串是在一定字长的限制下随机产生的。交叉算子作用在按交叉概率选中的两个染色体上,随机选中交叉位置,将两个染色体上对应于这些位置上的二进制数值进行交换,生成两个新的个体;而变异算子作用在按变异概率随机选中的个体上,一般是随机选定变异位,将该位的二进制值取反,生成一个新的个体
2.4 算法特点
①以决策变量的编码作为运算对象
②直接以目标函数值作为搜索信息(避开了函数求导的障碍)
③同时使用多个搜索点的搜索信息
④是一种基于概率的搜索技术(增加了其搜索过程的灵活性)
⑤具有自组织、自适应和自学习等特性
⑥同时,遗传算法具有可扩展性,易于同别的算法相结合,生成综合双方优势的混合算法
2.5 改进方向
标准遗传算法的主要本质特征,在于群体搜索策略和简单的遗传算子,这使遗传算法有诸多优点,成为一种具有良好适应性和可规模化的求解方法。
但是其存在局部搜索能力差和“早熟”等缺陷,不能保证算法收敛。
对遗传算法的改进,主要集中在对遗传算法的性能有重大影响的6个方面:编码机制、选择策略、交叉算子、变异算子、特殊算子和参数设计(包括群体规模、交叉概率、变异概率)等
此外,遗传算法与其他算法结合构成的混合遗传算法,可以做到优点综合,提高运行效率和求解质量
三.算法流程
①初始化:设置进化代数计数器t=0,设置最大进化代数T,随机生成M个个体作为初始群体P(0);
②个体评价:计算群体P(t)中各个个体的适应度;
③选择运算:将选择算子作用于群体。选择的目的是把优化的个体直接遗传到下一代或通过配对交叉产生新的个体再遗传到下一代。选择操作是建立在群体中个体的适应度评估基础上的;
④交叉运算:将交叉算子作用于群体。对选中的成对个体,以某一概率交换它们之间的部分染色体,产生新的个体。遗传算法中起核心作用的就是交叉算子;
⑤变异运算:将变异算子作用于群体。即是对群体中的个体串的某些基因座上的基因值作变动。群体P(t)经过选择、交叉、变异运算之后得到下一代群体P(t+1)
⑥终止条件判断:若t=T,则以进化过程中所得到的具有最大适应度个体作为最优解输出,终止计算;否则进行下一次遗传操作。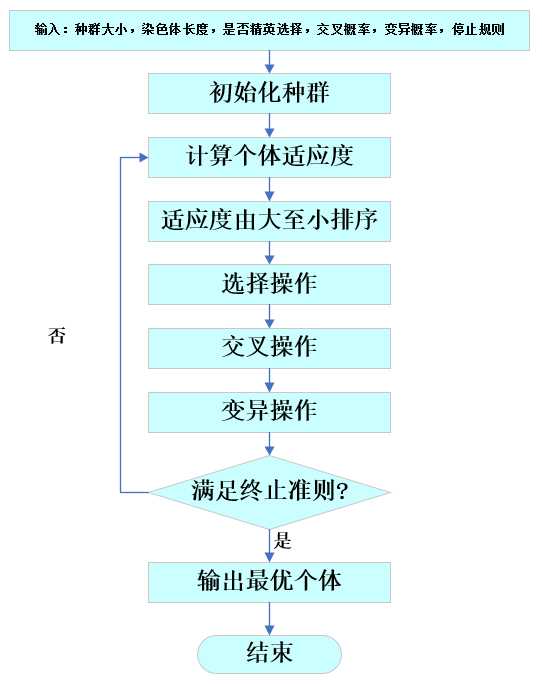
遗传算法运算流程图
四.关键参数
群体规模NP:
群体规模将影响遗传优化的最终结果以及遗传算法的执行效率。NP太小时,遗传优化性能一般不会太好。较大的NP可以减小遗传算法陷入局部最优解的机会,但往往意味着较高的计算复杂度。一般NP取10~100.
交叉概率Pc:
控制交叉操作被使用的频度。较大的交叉概率可以增强遗传算法开辟新的搜索区域的能力,但高性能的模式遭到破坏的可能性增大;若交叉概率太低,遗传算法搜索可能陷入迟钝状态。一般Pc取0.25~1.00.
变异概率Pm:
辅助性的搜索操作,主要目的是保持群体的多样性。一般低频度的变异可防止群体中重要基因的可能丢失,高频度的变异将使遗传算法趋于纯粹的随即搜索。通常Pm取0.001~0.1
运算的终止进化代数G:
表示遗传算法运行结束条件的一个参数。表示遗传算法运行到指定的进化代数之后就停止运行,并将当前群体中的最佳个体作为所求问题的最优解输出。一般视具体问题而定,G的取值可在100~1000之间。
五.MATLAB仿真实例
附:什么是P问题、NP问题和NPC问题(转自Matrix67)
原文:https://www.cnblogs.com/bitsjc/p/13634087.html