门电路
1、使用最少数量的两个输入与非门设计3输入与非门?
解析:Y=(ABC)’=((AB)’+C’)=(((AB)’)’C)’=((1(AB)’)’C)’,答案就出来了。
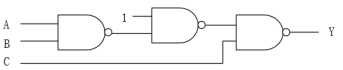
2、分别用两个输入的与非门实现OR GATE,AND GATE,画出门级电路。
分析: 或门,A+B = (A’B’)’=((1A)’(1B)’)’,三个与非门即可。
与门,AB=((AB)’)’,两个与非门即可。
3、画出assign out = (a[3:0] != 4’b0001)的门电路。
a[3:0] == 4’b0001 -> out = 1’b0;
a[3:0] != 4’b0001 -> out = 1’b1;
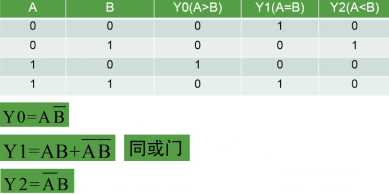
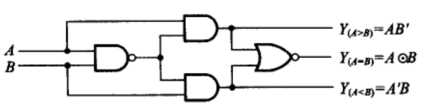
4、一位比较器的门电路实现,输出Y0(>)、Y1(=)、Y2(<)?
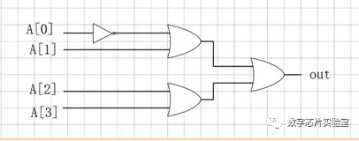
5、二选一选择器的门电路实现?
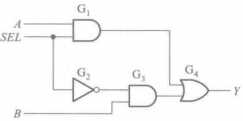
6、使用2x1MUX实现2输入AND门?
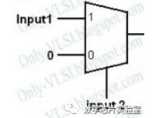
7、使用2x1MUX实现D锁存器?
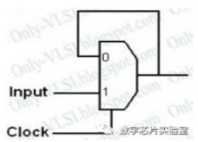
8、如果只使用2选1mux完成异或逻辑,至少需要几个mux?
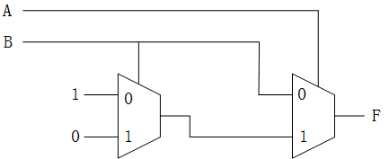
9、比较下面两个代码,利用FF、Mux、Adder、Dcmux等元件画出对应的框图,并比较这两个设计的不同以及优劣(注意:不要对加法器等进行细化处理,只要利用现有的模块,如DFF、Adder、减法器等)
(1)Always @(A or B or C or D) Sum = sel ?(A+B):(C+D) (2)always @(A or B or C or D) begin Switch0 = sel ? A:C; Switch1 = sel ? B:D; end assign sum = Switch0+Switch1;
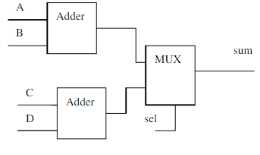
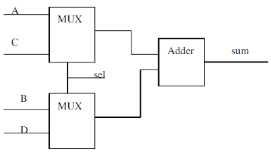
很明显第二种比第一种少了一个加法器,资源消耗减少,说明一个好的设计可以减少资源的占用,提高资源的利用率。
10、相同工艺条件下,下列哪种逻辑的组合逻辑延迟最长(A)
A、2输入异或门 B、2输入与非门
C、2输入或门 D、1输入反相器
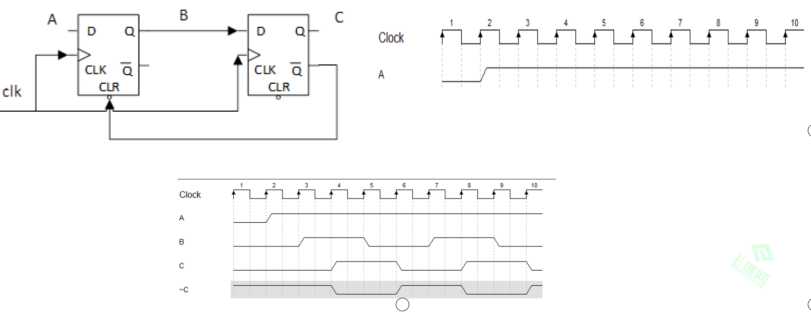
11、根据 A 的波形,画出 B、C 的波形,寄存器是同步清0的。
加法器专题
1、加法器分类
(1)半加器;
(2)全加器;
(3)进位延时加法器;
(4)进位保留加法器;
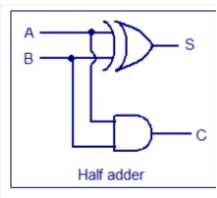
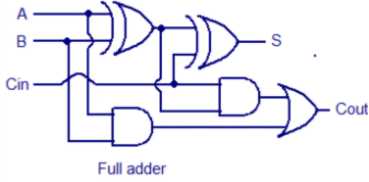
2、半加器和全加器结构
半加器:两个1位二进制相加,不考虑低位进位;
全加器:两个1位二进制相加,考虑低位进位;
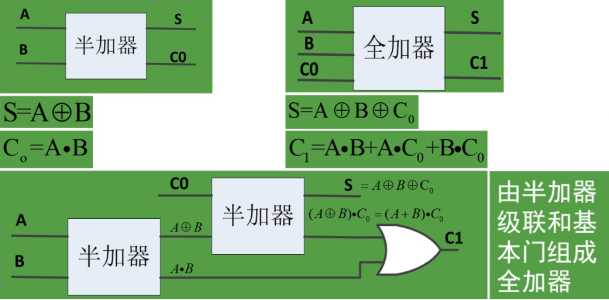
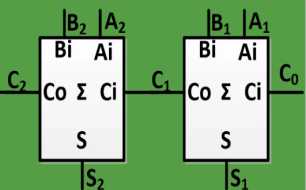
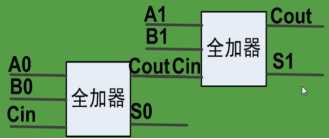
3、行波进位加法器RCA(串行进位加法器、逐位进位加法器)
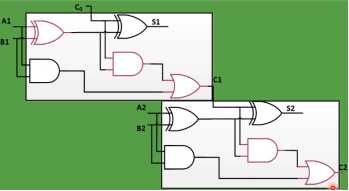
4、超前进位加法器
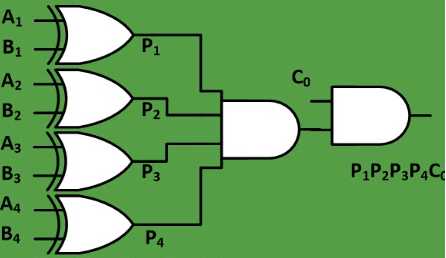
5、下图是一个全加器的电路图,假设每个门的延时为T,不考虑线延时的扇入扇出,下列说法正确的是(AD)
A) 4位Ripple-Carry Adder的最大延时为9T
B) 8位Ripple-Carry Adder的最大延时为9T
C) 4位Carry-Lookahead Adder的最大延时为3T
D) 8位Carry-Lookahead Adder的最大延时为4T
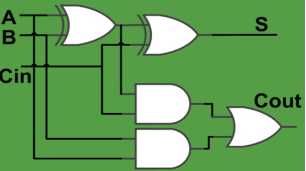
分析:首先明白两种加法器的结构,首先分析 Ripple-Carry Adder的结构,2bit的R加法器就是两个R加法器连接起来,如下图所示:
将这个图代入题干,可以得出最大延时是A到Count,然后再一个Cin到Count,即3+2=5,每再添一个R加法器,最长路径多2个门,因此4位R加法器最大延时为3+2+2+2=9;其次分析Carry-Lookahead Aheader的特点,C加法器的各级进位彼此独立产生,只与输入数据和Cin有关,因此超过1位的C加法器,其最大延时都是3位本体最大延时加上1位的进位延时,因此8位的C加法器的最大延时为3+1=4。(很多人分析的是3,他只算了输入到进位,但我们求的是和,所以得加一)。
6、加法器代码
//-------------------------------------------------------- //-- 半加器 //-------------------------------------------------------- module HALF_ADDER ( input wire a, input wire b, output reg s, output reg c ); always@(*)begin c = a & b; s = a ^ b; end endmodule //-------------------------------------------------------- //-- 全加器 //-------------------------------------------------------- module FULL_ADDER ( input wire ai, input wire bi, input wire ci, output reg s, output reg co ); wire gi; wire pi; wire pi_ci; wire si; HALF_ADDER U_HALF_ADDER_0 ( .a (ai ), .b (bi ), .c (gi ), .s (pi ) ); HALF_ADDER U_HALF_ADDER_1 ( .a (ci ), .b (pi ), .c (pi_ci ), .s (si ) ); always@(*)begin co = pi_ci | gi; s = si; end endmodule //-------------------------------------------------------- //-- 行波进位加法器 //-------------------------------------------------------- module RCA #( parameter N = 4) ( input wire [N-1:0] ai, input wire [N-1:0] bi, input wire ci, output wire [N-1:0] s, output wire co ); reg [N-1:0] ci_t; wire [N-1:0] co_t; always@(*)begin:ci_gen integer n; for(n = 0; n < N; n = n + 1)begin if(n == 0) ci_t[n] = ci; else ci_t[n] = co_t[n-1]; end end assign co = co_t[N-1]; genvar i; generate for(i = 0; i < N; i = i + 1)begin:rca_g FULL_ADDER U_FULL_ADDER ( .ai (ai[i] ), .bi (bi[i] ), .ci (ci_t[i] ), .co (co_t[i] ), .s (s[i] ) ); end endgenerate endmodule //-------------------------------------------------------- //-- 超前进位加法器 //-------------------------------------------------------- module CLA #( parameter N = 4) ( input wire [N-1:0] ai, input wire [N-1:0] bi, input wire ci, output reg [N-1:0] s, output reg co ); reg [N:0] c; reg [N:1] st; reg [N:1] g; reg [N:1] p; reg [N:1] a; reg [N:1] b; reg gp; reg gg; always@(*)begin s = st; a = ai; b = bi; co = c[N]; end always@(*)begin:cla_gen integer i; gp = 1; gg = 0; c[0] = ci; for(i=1; i<=N; i=i+1)begin g[i] = a[i] & b[i]; p[i] = a[i] ^ b[i]; gp = p[i] & gp; gg = g[i] + (p[i] & gg); c[i] = gg | (gp & c[i-1]); st[i] = p[i] ^ c[i-1]; end end endmodule
原文:https://www.cnblogs.com/xianyufpga/p/13642359.html