面试官问我什么是「栈」，我随手画了10张图来解释

栈的概念

栈（stack）是限定仅在表的一端进行操作的数据结构，且栈是一种先进后出的数据结构，允许操作的一端称为栈顶，不允许操作的称为栈底，如下图所示：

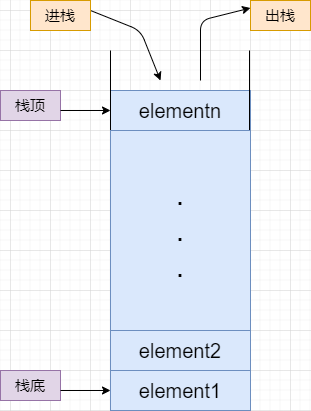
之前我们讲到了链表，我们只能够对其链表的表尾结点进行操作，并且只能进行插入一个新的结点与删除最末尾的这个结点两个操作，而这样强限制性的‘链表’，就是我们所说的栈。

就像是一个死胡同一样，只有一个出口，如图所示，有个概念：

栈的结点设计

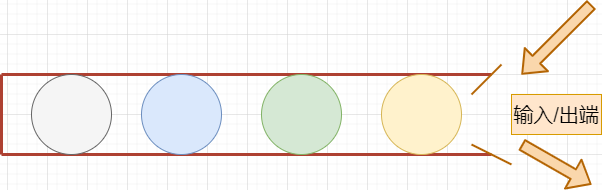
栈分为数组栈和链表栈，其区别如下：

• 数组栈使用数组进行功能的模拟，实现较为快速和便利；

• 链表栈使用链表的思路去设计，实现相比较说较为麻烦，但是其稳定，且不易出错；

在链表栈中又分为静态链表栈和动态链表栈，其区别如下：

• 静态链表栈给定栈的空间大小，不允许超过存储超过给定数据大小的元素；

• 动态栈使用的是自动创建空间的方法进行创建，只要符合机器的硬件要求以及编译器的控制，其理论上是极大的。

数组栈

其实际就是用一段连续的存储空间来存储栈中的数据元素，有以下特点：

1. 元素所占的存储空间必须连续，这里的连续是指的逻辑连续，而不是物理连续。

2. 元素在存储空间的位置是按逻辑顺序存放的

我们来举例说明，鉴于C语言数组下标都是0开始，并且栈的使用需要的空间大小难以估计，所以初始化空栈的时候，不应该设定栈的最大容量。

我们先为栈设定一个基本容量，在应用过STACK_程当中，当栈的空间不够用时，再逐渐扩大。

设定2个常量，STACK_INIT_SIZE(存储空间初始化分配量)和STACK_INCREMENT(存储空间分配增量),宏定义如下

#define STACK_INIT_SIZE 1000 //数值可以根据实际情况确定
#define STACK_INCREMENT 10   //数值可以根据实际情况确定

栈的定义如下

typedef struct      
{
    void *base; 
    void *top;
    int stackSize;
} SqSTACK;

• base 表示栈底指针

• top 表示栈顶指针

• stackSize 表示栈当前可以使用的最大容量

若base的值是NULL，表示栈结构不存在;top初始值指向栈底，即top = base;

每当插入新的元素时，指针top就增1，反之删除就减1，非空栈中的栈顶指针始终在栈顶元素的下一个指针上面。

数据元素和栈顶指针的关系如下图所示：

链表栈

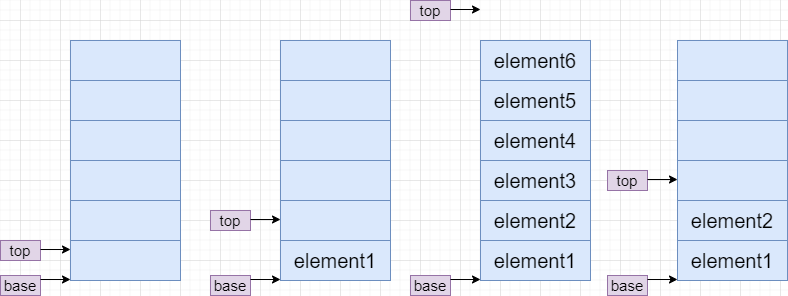
我们以链表栈的动态链表栈为例子，进行栈的设计。

首先是栈的结点，设计出两个结构体，一个结构体Node表示结点，其中包含有一个data域和next指针，如图所示：

Node

其中data表示数据，next指针表示下一个的指针，其指向下一个结点，通过next指针将各个结点链接。

接下来是我们设计的重点，为这个进行限制性的设计，我们需要额外添加一个结构体，其包括了一个永远指向栈头的指针top和一个计数器count记录元素个数。

其主要功效就是设定允许操作元素的指针以及确定栈何时为空，如图所示：

Stack

这里我采用的是top和count组合的方法。其代码可以表示为：

//栈的结点设计
//单个结点设计，数据和下一个指针
typedef struct node     
{
    int data; 
    struct node *next;
} Node;

利用上面的结点创建栈，分为指向头结点的top指针和计数用的count

typedef struct stack    
{
    Node *top;
    int count;
} Link_Stack;

栈的基本操作—入栈（压栈）

入栈的基本顺序可以用以下图所示：

入栈(push)操作时，我们只需要找到top所指向的空间，创建一个新的结点，将新的结点的next指针指向top指针指向的空间，再将top指针转移，并且指向新的结点，这就是是入栈操作。

其代码可以表示为：

//入栈 push
Link_Stack *Push_stack(Link_Stack *p, int elem)
{
    if (p == NULL)
        return NULL;
    Node *temp;
    temp=(Node*)malloc(sizeof(Node));
    //temp = new Node;
    temp->data = elem;
    temp->next = p->top;
    p->top = temp;
    p->count++;
    return p;
}

栈的基本操作—出栈

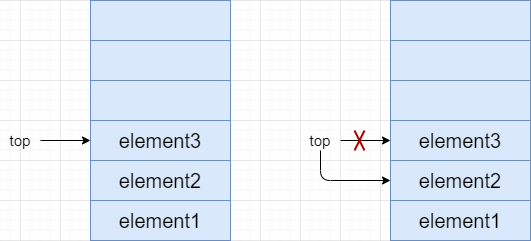
出栈（pop）操作，是在栈不为空的情况下，重复说一次，一定要进行判空操作，将栈顶的元素删除，同时top指针，next向下进行移动即可的操作。

其代码可以表示为：

//出栈 pop
Link_Stack *Pop_stack(Link_Stack *p)
{
    Node *temp;
    temp = p->top;
    if (p->top == NULL)
    {
        printf("错误：栈为空");
        return p;
    }
    else
    {
        p->top = p->top->next;
        free(temp);
        //delete temp;
        p->count--;
        return p;
    }
}

栈的基本操作—遍历

这个就很常见了，也是我们调试必须的手段。

栈的遍历相对而言比较复杂，由于栈的特殊性质，其只允许在一端进行操作，所以遍历操作操作永远都是逆序的。

简单一点描述，其过程为，在栈不为空的情况下，一次从栈顶元素向下访问，直到指针指向空（即到栈尾）为结束。

其代码可以表示为：

//遍历栈：输出栈中所有元素
int show_stack(Link_Stack *p)
{
    Node *temp;
    temp = p->top;
    if (p->top == NULL)
    {
        printf("");
        printf("错误：栈为空");
        return 0;
    }
    while (temp != NULL)
    {
        printf("%d\t", temp->data);
        temp = temp->next;
    }
    printf("\n");
    return 0;
}

栈数组与栈链表的代码实现

最后呢，我们使用代码来帮助我们了解一下：

栈数组

数组栈是一种更为快速的模拟实现栈的方法，这里我们不多说。

模拟，就是不采用真实的链表设计，转而采用数组的方式进行模拟操作。

也就是说这是一种仿真类型的操作，其可以快速的帮助我们构建代码，分析过程，相应的实现起来也更加的便捷。

其代码如下:

#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#define maxn 10000
 
//结点设计
typedef struct stack{
    int data[maxn];
    int top;
}stack;
 
//创建
stack *init(){
    stack *s=(stack *)malloc(sizeof(stack));
    if(s==NULL){
        printf("分配内存空间失败");
        exit(0);
    }
    memset(s->data,0,sizeof(s->data));
    //memset操作来自于库文件string.h，其表示将整个空间进行初始化
    //不理解可以查阅百度百科https://baike.baidu.com/item/memset/4747579?fr=aladdin
    s->top=0;     //栈的top和bottom均为0（表示为空）
    return s;
}
 
//入栈push
void push(stack *s,int data){
    s->data[s->top]=data;
    s->top++;
}
 
//出栈pop
void pop(stack *s){
    if(s->top!=0){
        s->data[s->top]=0;  //让其回归0模拟表示未初始化即可
        s->top--;
    }
}
 
//模拟打印栈中元素
void print_stack(stack *s){
    for(int n=s->top-1;n>=0;n--){
        printf("%d\t",s->data[n]);
    }
    printf("\n");   //习惯性换行
}
 
int main(){
    stack *s=init();
    int input[5]={11,22,33,44,55};  //模拟五个输入数据
    for(int i=0;i<5;i++){
        push(s,input[i]);
    }
    print_stack(s);
    /////////////
    pop(s);
    print_stack(s);
    return 0;
}

其编译结果如下：

栈链表

#include <stdio.h>
#include <stdlib.h>
//栈的结点设计
//单个结点设计，数据和下一个指针
typedef struct node     
{
    int data; 
    struct node *next;
} Node;
//利用上面的结点创建栈，分为指向头结点的top指针和计数用的count
typedef struct stack    
{
    Node *top;
    int count;
} Link_Stack;
 
//创建栈
Link_Stack *Creat_stack()
{
    Link_Stack *p;
    //p = new Link_Stack;
    p=(Link_Stack*)malloc(sizeof(Link_Stack));
    if(p==NULL){
        printf("创建失败，即将退出程序");
        exit(0);
    }
 else
 {printf("创建成功\n");
 }
    p->count = 0;
    p->top = NULL;
    return p;
}
 
//入栈 push
Link_Stack *Push_stack(Link_Stack *p, int elem)
{
    if (p == NULL)
        return NULL;
    Node *temp;
    temp=(Node*)malloc(sizeof(Node));
    //temp = new Node;
    temp->data = elem;
    temp->next = p->top;
    p->top = temp;
    p->count++;
    return p;
}
 
//出栈 pop
Link_Stack *Pop_stack(Link_Stack *p)
{
    Node *temp;
    temp = p->top;
    if (p->top == NULL)
    {
        printf("错误：栈为空");
        return p;
    }
    else
    {
   printf("\npop success");
        p->top = p->top->next;
        free(temp);
        //delete temp;
        p->count--;
        return p;
    }
}
 
//遍历栈：输出栈中所有元素
int show_stack(Link_Stack *p)
{
    Node *temp;
    temp = p->top;
    if (p->top == NULL)
    {
        printf("");
        printf("错误：栈为空");
        return 0;
    }
    while (temp != NULL)
    {
        printf("%d\t", temp->data);
        temp = temp->next;
    }
    printf("\n");
    return 0;
}
 
int main()
{ //用主函数测试一下功能
 int i;
    Link_Stack *p;
    p = Creat_stack();
    int n = 5;
    int input[6] = {10,20,30,40,50,60};
    /////////////以依次入栈的方式创建整个栈//////////////
    for(i=0;i<n;i++){
        Push_stack(p, input[i]);
    }
    show_stack(p);
    ////////////////////出栈///////////////////////
    Pop_stack(p);
    show_stack(p);
    return 0;
}

编译结果如下：

关于栈的总结

栈-它是一种运算受限的线性表，在数制转换，括号匹配的检验，表达式求值等方面都可以使用，并且较为简便的解决问题。

今天栈基础就讲到这里，下一期，我们再见！

来源：站长资讯中心

面试官问我什么是「栈」，我随手画了10张图来解释

原文：https://www.cnblogs.com/0591jb/p/13642378.html