本文提出了一种六面体体细分的方案,可以将六面体分成比较光顺的六面体。同时增加六面体的数量且不改变六面体的拓扑。
本文作者 Bajaj =.=
主要由两个步骤组成 split & average
将CC四边形细分变为简单的方案可以通过 bi-linear subdivision followed by a simple averaging operation.
一个双线性细分然后跟着一个均值的操作。
简单来说差值细分,作者没有对于表面点进行详细的说明。
但是对于内部的点
作者提出了一种mask的思想。
找到一篇文章讲mask的思想。就是新产生的点的权重的确定的矩阵
More precisely:
? What are good averaging masks?
? The averaging mask determines the weights by which the new point positions are computed

对于一个面来说,mask矩阵就是中心点和它四个角的加权平均
不知道能否这么解释。
核心语句 reposition a vertex at the centroid of the centroids of the eight hexahedra that contain the vertex.
对于在中心点来说,一个点连接着8个cell(六面体),如何移动这个顶点的坐标呢?首先求这8个cell的重心(每个cell8个顶点的均值),
求出8个cell均值,然后8个cell均值的均值,也就是这个点应在存在的位置了。 下图的公式就是对于这个思想的简单解释了

但是核心的是如何确定边缘的点,边缘的点只连接了4个cell,如果采用上述方法,那么将导致急剧的收缩。
所以作者在2.3节提出了复合细分规则。
\(ring[v1, v2..]\) 表示一些列顶点的多面体
\(val[v1,v2..]\) 表示这一系列点含有的多面体的个数。
\(dim[v1, v2..]\) 表示最小的维度 0 表示他们重合在了一起,1表示他们在边上,2表示他们在公共面上。
对于一个旧顶点,他的新坐标表示在周围一圈旧多面体的加权求和上。
作者提出了这个公式
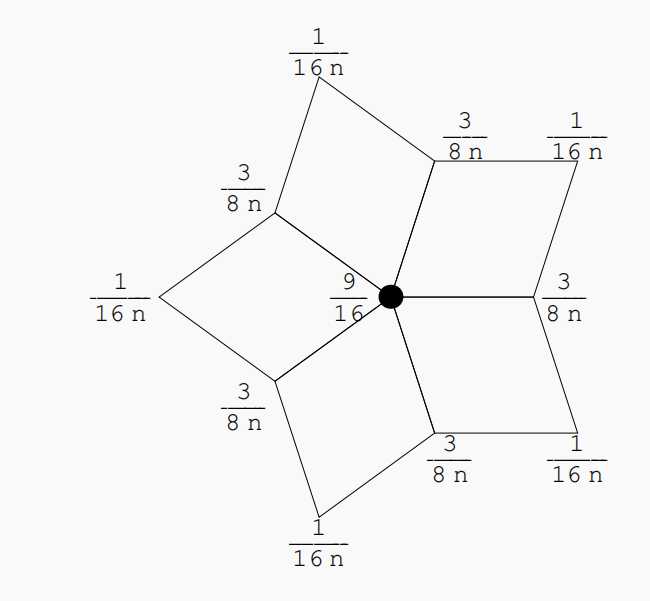
这个图就是对于公式的应用。
n表示中心黑点的度,也就是中心黑点和几个四边形相互连接。
如果只有一个四边形的话,那么 n = 1, val[v] = 1
\(\frac{1}{16} = \frac{1}{4^2 * 1} * 3^{2-2} * 1\) 因为共面所以dim=2, val[u,v] = 1 是因为包含u,v的顶点的面只有一个面。
对于数学没有太敏感的我,没什么软用。
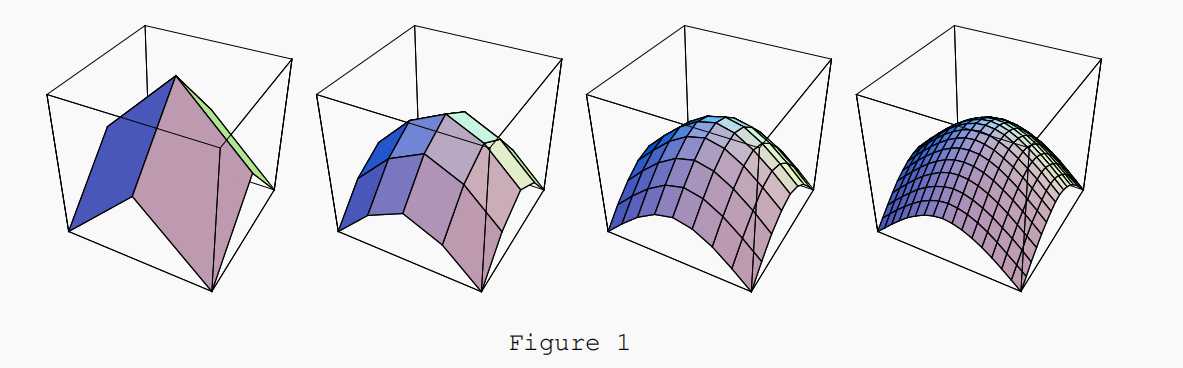
演示了对于面进行split & average 之后的结果。然后作者依据这种现象构建了新的六面体细分方案。
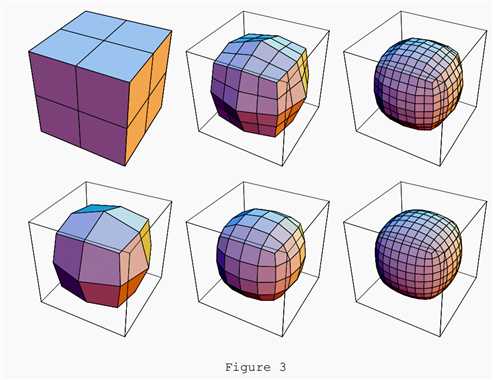
可以通过上面的图看出来有两个操作,一个是简单的差值,另一个是average。中间的图是差值的操作。
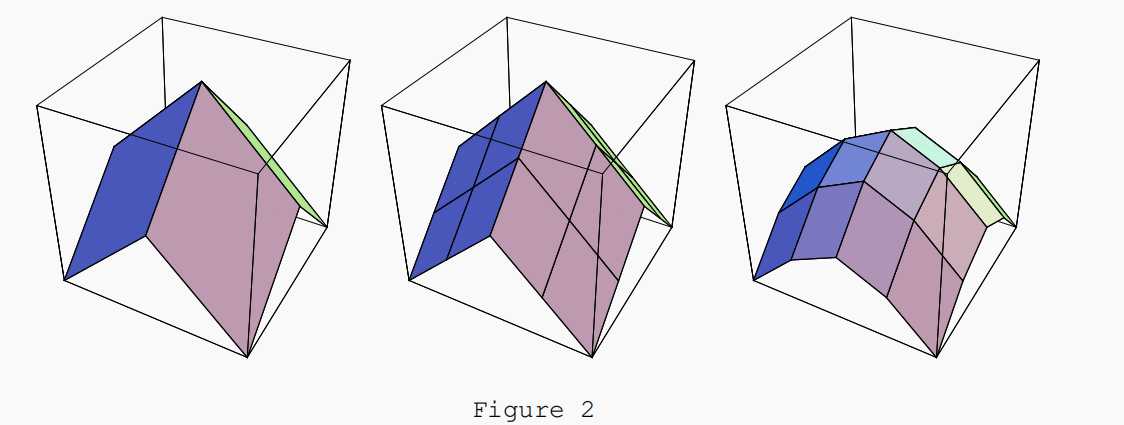
上面一行是差值,下面一行是average的效果图。
Unfortunately, these rules only apply to quadrilateral meshes with tensor product topology (i.e. each
interior vertex is shared by four quadrilaterals). 作者说,简单的四边形细分规则,只能应用于张量积形式的拓扑(作者举了一个例子,就是内部点,周围有四个顶点。)
可以应用于非流形拓扑,证明了这种方案生成的六面体网络的连续性。
文章的难点 均分可以解决内部点的问题如何将表面的点进行均分???
参考链接 https://www.cnblogs.com/sybil-hxl/p/12804765.html
https://img2020.cnblogs.com/blog/968024/202005/968024-20200515231824101-870579029.png
猜测 应该是沿着两个维度进行细分
类比3线性细分 应该是沿着三个维度进行细分
文献阅读 A Subdivision Scheme for Hexahedral Meshes
原文:https://www.cnblogs.com/eat-too-much/p/13642865.html