The Biggest Triangle-布布扣-bubuko.com

题目描

Three in?nite lines de?ne a triangle, unless they meet at a common point or some of them are parallel.

Given a collection of in?nite lines, what is the largest possible perimeter of a triangle de?ned by some three lines in the collection?

输入

The ?rst line of input contains a single integer n (3 ≤ n ≤ 100) indicating the number of in?nite lines.
The next n lines describe the collection of in?nite lines. The ith such line contains four integers x1, y1, x2, y2 (−10 000 ≤ x1, y1, x2, y2 ≤ 10 000) where (x1, y1) ≠ (x2, y2) are two points lying on the ith in?nite line.

输出

Display a single real value which is the perimeter of the largest triangle that can be formed from three of the in?nite lines. Your output will be considered correct if it is within an absolute or relative error of 10−5 of the correct answer.
If no triangle can be formed using the given lines, then you should instead display the message no triangle.

样例输入

样例输出

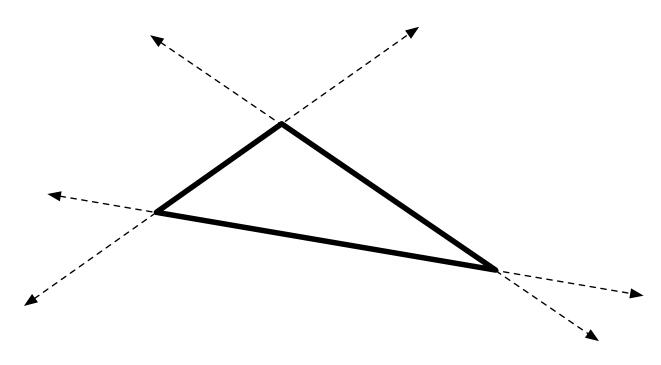
【样例1】
3.4142135624
【样例2】
no triangle
【样例3】
12.0000000000

 1 #include <cmath>
 2 #include <cstdio>
 3 #include <iostream>
 4 #include <algorithm>
 5 #define EPS 1e-9
 6 using namespace std;
 7 typedef double DB;
 8 struct Point
 9 {
10     Point(){}
11     Point(DB x,DB y):x(x),y(y){}
12     DB x, y;
13 };
14 struct Vector
15 {
16     Vector(){}
17     Vector(DB x,DB y):x(x),y(y){}
18     DB x, y;
19 };
20 int n;
21 Point g[109][3];
22 DB Cross(Vector a, Vector b)
23 {
24     return a.x*b.y-a.y*b.x;
25 }
26 DB Area(Point a, Point b, Point c)
27 {
28     return abs(Cross(Vector(b.x-a.x, b.y-a.y), Vector(c.x-a.x, c.y-a.y)));
29 }
30 Point getPoi(int i, int j)
31 {
32     DB s1 = Area(g[i][1], g[i][2], g[j][1]);
33     DB s2 = Area(g[i][1], g[i][2], g[j][2]);
34     DB k1 = Cross(Vector(g[i][2].x-g[i][1].x, g[i][2].y-g[i][1].y), Vector(g[j][1].x-g[i][1].x, g[j][1].y-g[i][1].y));
35     DB k2 = Cross(Vector(g[i][2].x-g[i][1].x, g[i][2].y-g[i][1].y), Vector(g[j][2].x-g[i][1].x, g[j][2].y-g[i][1].y));
36     Vector G = Vector(g[j][2].x-g[j][1].x, g[j][2].y-g[j][1].y);
37     if(k1*k2>0)
38         return Point(g[j][1].x-G.x*s1/(s2-s1), g[j][1].y-G.y*s1/(s2-s1));
39     else
40         return Point(g[j][1].x+G.x*s1/(s1+s2), g[j][1].y+G.y*s1/(s1+s2));
41 }
42 DB getDis(Point a, Point b)
43 {
44     return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
45 }
46 DB calc(int i, int j, int k)
47 {
48     Vector a, b, c;
49     a = Vector(g[i][2].x-g[i][1].x, g[i][2].y-g[i][1].y);
50     b = Vector(g[j][2].x-g[j][1].x, g[j][2].y-g[j][1].y);
51     c = Vector(g[k][2].x-g[k][1].x, g[k][2].y-g[k][1].y);
52     DB A = abs(Cross(a, b)), B = abs(Cross(a, c)), C = abs(Cross(b, c));
53     if(A<EPS || B<EPS || C<EPS) return -1e9;
54     Point X = getPoi(i, j), Y = getPoi(i, k), Z = getPoi(j, k);
55     DB dA = getDis(X, Y), dB = getDis(X, Z), dC = getDis(Y, Z);
56     if(dA+dB+dC > EPS) return dA+dB+dC;
57     else return -1e9;
58 
59 }
60 int main()
61 {
62     scanf("%d", &n);
63     for(int i = 1; i <= n; i++)
64         scanf("%lf%lf%lf%lf", &g[i][1].x, &g[i][1].y, &g[i][2].x, &g[i][2].y);
65     DB ans = -1e9;
66     for(int i = 1; i <= n; i++)
67         for(int j = i+1; j<= n; j++)
68             for(int k = j+1; k <= n; k++)
69                 ans = max(ans, calc(i, j, k));
70     if(ans > EPS) printf("%.10lf\n", ans);
71     else puts("no triangle");
72     return 0;
73 }

View Code