#浮点数的表示
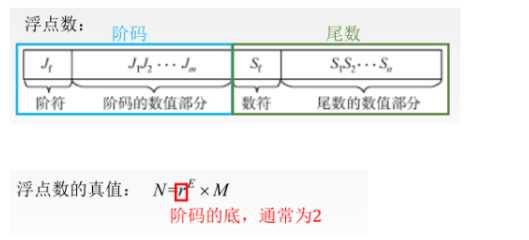
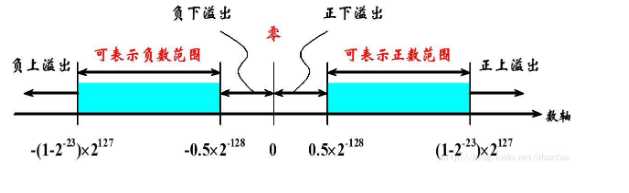
阶码:阶码是整数,阶符和 m 位阶码的数值部分共同反映 浮点数的表示范围及小数点的实际位置 ,常用移码或补码表示。IEEE754标准中采用移码的表示形式。 尾数:数符表示浮点数的符号,尾数的数值部分的位数 n 反映浮点数的 精度 ,常用原码或补码表示。IEEE754标准中采用原码的表示形式。

左规:当浮点数运算的结果为非规格化时要进行规格化处理,将尾数算术左移一位,阶码减1(基数为2时)。
右规:当浮点数运算的结果尾数出现溢出(双符号位为01或10)时,将尾数算术右移一位,阶码加1(基数为2时)。

当浮点数尾数的基数为2时,原码规格化数的尾数最高位一定是1,补码规格化数的尾数最高位一定与尾数符号位相反,基数不同,浮点数的规格化形式也不同。当基数为4时,原码规格化形式的尾数最高两位不全为0,当基数为8时,原码规格化形式的尾数最高3位不全为0。


 #补充:变形补码
###概念:变形补码,又称”模4补码“即用两个二进制位来表示数字的符号位,其余与补码相同。变形补码,用“00”表示正,用“11”表示负,也称为模4的补码。用变形补码进行加减运算时,当运算结果的符号位出现“01”或者“10”时,则表示产生溢出。变形补码的最高位(第一个符号位)总是表示正确的符号,比如"00"、 “01”分别表示正数、正溢出(上溢),"11"、“10”表示负数、负溢出(下溢)。
##示例:
1、产生01的情况:
补码:
0 111
+ 0 010
————
1 001
两个正数相加出现了负数,明显有误,就是说此时产生了上溢出(注:补码运算时符号位也参与运算)
变形补码:
00 111
+ 00 010
————
01 001
此时读数时,由于左边的符号位是0,所以表示正数,读成+9,而不像模二补码中变成了-7
2、产生10的情况:
补码:
1 001
+ 1 010
————
10 011
溢出一位后,结果变成了0 011,两个负数相加出现了正数,明显有误,就是说此时产生了下溢出(注:补码运算时符号位也参与运算)
变形补码:
11 001
+ 11 010
————
110 011
溢出一位后,结果变成了10 011,此时读数时,由于左边的符号位是1,所以表示负数,读成-3,而不像模二补码中变成了+3
(注:产生01和10时,读数时右边那一位符号也要算在数字里面)
#补充:变形补码
###概念:变形补码,又称”模4补码“即用两个二进制位来表示数字的符号位,其余与补码相同。变形补码,用“00”表示正,用“11”表示负,也称为模4的补码。用变形补码进行加减运算时,当运算结果的符号位出现“01”或者“10”时,则表示产生溢出。变形补码的最高位(第一个符号位)总是表示正确的符号,比如"00"、 “01”分别表示正数、正溢出(上溢),"11"、“10”表示负数、负溢出(下溢)。
##示例:
1、产生01的情况:
补码:
0 111
+ 0 010
————
1 001
两个正数相加出现了负数,明显有误,就是说此时产生了上溢出(注:补码运算时符号位也参与运算)
变形补码:
00 111
+ 00 010
————
01 001
此时读数时,由于左边的符号位是0,所以表示正数,读成+9,而不像模二补码中变成了-7
2、产生10的情况:
补码:
1 001
+ 1 010
————
10 011
溢出一位后,结果变成了0 011,两个负数相加出现了正数,明显有误,就是说此时产生了下溢出(注:补码运算时符号位也参与运算)
变形补码:
11 001
+ 11 010
————
110 011
溢出一位后,结果变成了10 011,此时读数时,由于左边的符号位是1,所以表示负数,读成-3,而不像模二补码中变成了+3
(注:产生01和10时,读数时右边那一位符号也要算在数字里面)原文:https://www.cnblogs.com/just-like-me/p/13656774.html