我们将从 \(b\) 投影到 \(a\) 说起,\(a\) 上离 \(b\) 点最近的点是 \(p\) ,\(bp\) 垂直于 \(a\) ,距离 \(e=b-p\) (向量减法),\(p\) 就是投影点。
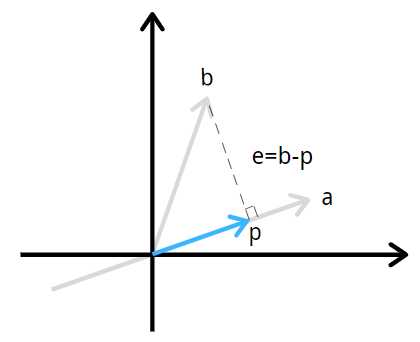
向量 \(p\) 就是 \(b\) 在 \(a\) 的投影。关键就是垂直。
\(p\) 是 \(a\) 的某个倍数。我们可以记为 \(p=xa\) .
\(x\) 就是我们要找的。
因为 \(a\) 与 \(e\) 垂直,可得
展开得
从矩阵乘法可以知道(一行点乘一列), \(a^Ta\) 是一个数字,所以我们可以两边同时除以 \(a^Ta\)
所以 \(p\) 可以表示为
先消化一下这个式子
若 \(b\) 翻了一倍变成 \(2b\) ,投影 \(p\) 也变成 \(2\) 倍。
若 \(a\) 变成 \(2a\) ,投影 \(p\) 不变。从几何看,就是 \(p\) 还是那个位置;从 \(p\) 式子上看,分母和分子会乘以相同倍数,抵消掉了。
让我们从矩阵角度思考这个式子,投影 \(p\) 是一个投影矩阵作用于某个向量。我们将投影矩阵记为 \(P\) ,该例子作用于 \(b\) :
而且可知
她不等于 \(1\) ,因为分母是行乘列,结果一个数字,而分子是列乘行,结果是一个矩阵。
如果 \(a\) 是 $ n$ 维,那么 \(a.a^T\) 是 \(n*n\) 矩阵。
\(P\) 将 \(b\) 投影于 \(a\) ,是这个矩阵生成了投影。
列空间定义告诉我们,无论把矩阵乘以什么,最终都会停留在该列空间,所以\(P\) 乘以任何向量 \(b\) ,最终都会停留在 \(P\) 的列空间 \(C(A)\).
\(C(A)\) 是通过 \(a\) 的一条直线。
\(P\) 的秩是 \(1\).
\(P\) 是对称矩阵,有 \(P^T=P\)
将 \(b\) 投影两次,第二次投影的结果和第一次一样,投影还是在相同的位置,有 \(P^2=P\)
上一解我们就讨论过,\(Ax=b\) 也许无解。而我们希望利用上所有的数据,问题就在于怎么微调 \(b\) .
我们可以将 \(b\) 变为列空间中最接近她的那一个,把无解变成有解,将\(Ax=b\) 变为
其中,\(p\) 是 \(b\) 在列空间上的投影。
\(\hat x\) 不同于 \(x\) ,因为 \(x\) 是不存在的,\(\hat x\) 表示的是最接近结果的解。
解决 \(Ax=b\) 无解问题,我们首先需要找到列空间中最接近 \(b\) 的是什么,这就是投影的意义。
一维中,我们将 \(b\) 投影到 \(a\) ,求得 \(a\) 空间中距离 \(b\) 最近的向量 \(p\).
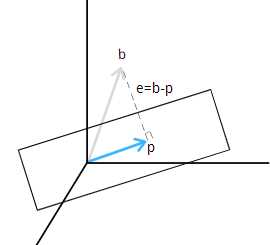
我们将其与方程 \(Ax=b\) 联系起来。平面是 \(A\) 的列空间\(C(A)\),
\(a_1、a_2\)线性无关构成 \(C(A)\) 的一组基。
若 \(b\) 在 \(C(A)\) 里面,投影结果就是 \(b\) 自己。但显然,上图向量 \(b\) 不在 \(C(A)\) 里面。我们希望找到将 \(b\) 投影到平面上最近点的漂亮公式。
通常有一个误差向量 \(e=b-p\) ,一般不为零。当 \(e\) 垂直于平面时长度最小。
\(p\) 在 \(C(A)\) 中,所以 \(p\) 可以由平面的基向量表示为
所以我们的问题到这里就转换为,寻找合适的 \(A\) 的列组合,让 \(e=b-p=b-A\hat x\) 垂直于平面。
由于 \(e\) 垂直于平面, 所以\(e\) 垂直于平面里面任意向量,可得
可以将其表示为矩阵形式:
等价于
\(e\) 位于 左零空间 \(N(A^T)\) .由上节课可知,左零空间和列空间是正交关系,所以 \(e\) 垂直于 \(A\) 的列空间。
现在开始解方程 \(A^T(b-A\hat x)=0\)
展开:
两边同时乘以 \((A^TA)^{-1}\),
这就是方程的解。
投影 \(p\) 的公式为:
投影矩阵 \(P\) :
\(\hat x、p、P\) 这三个公式适用于 \(n\) 维情况。
需要注意的是,如果矩阵 \(A\) 不是方阵,那么 \(A^{-1}\) 是不存在的,所以我们不能把 \((A^TA)^{-1}\) 展开,只能保留。
和一维一样,同样存在
\(P^T=P\)
\(P^2=P\)
证明过程改变乘法顺序,就能得到单位阵消掉,不再累述。
最常见的例子是通过最小二乘法拟合一条直线。
比如,我们现在有3个点,\((1,1)、(2,2)、(3,2)\),横坐标表示时间 \(t\) ,纵坐标bi表示数据 \(b\) .我们希望求出 "最优的直线",误差越小越好。
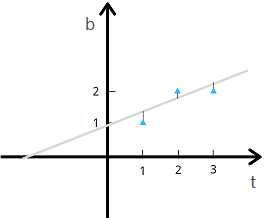
设最优直线为 \(b=C+Dt\) ,我们的目标就是求出 \(C、D\)。
根据三个点我们可以得到三个方程:
从而可以得到 \(Ax=b\) 的矩阵形式:
注意这个方程无解。但我们可以求出最优解。
我们将两边同时乘以\(A^T\),通过投影获得一个有解的方程。
下节课继续。
原文:https://www.cnblogs.com/ckk-blog/p/13658849.html