最简单的方法是将矩阵先转置,然后翻转每一行元素,就得到旋转90°的矩阵了
我用的另一种思路,就是真的旋转
例如如下矩阵
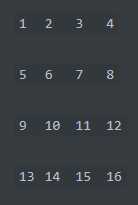
然后先旋转最外层:

然后再旋转内层

也就是每个元素挪动到它最终的位置上,并用临时变量存储被占用位置的元素,每一次需要挪动元素个数4个
最外层的循环是从1 2 3这三个元素开始的
到了内层,它的开始元素的个数少了2个,就只剩1个,也就是6
当开始元素没有了,那么我们的递归思路就可以退出了
顺时针旋转90°的坐标变化如下:
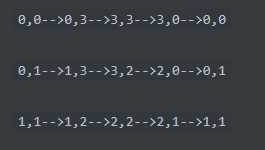
总结就是加入下标从0开始,0-n*0-n的矩阵
那么坐标(i,j)旋转以后的位置是(j,n-i)
使用递归的方式,按照每次开始元素数量减少两个的方式直到没有开始元素退出递归
找到一个开始旋转的元素,按照上面的坐标变换关系,变换4次
继续下一个开始元素,直到所有开始元素旋转完成
进入下一层递归,开始元素数量减少两个
func rotate(matrix [][]int) {
length := len(matrix)
var interRotateFunc func(n int)
interRotateFunc = func(n int) {
if (length - n) > 1 {
//首先旋转最外层
// 因为这几个开始的元素具有相同的横坐标,所以将他们的横坐标固定
stableRow := n / 2
for i := stableRow; i < length-stableRow-1; i++ {
// 开始元素所在那一行的最后一个元素会被开始元素的第一个元素占据位置,所以这最后一个不能作为开始元素
// 每一次要替换4个元素的位置
tmp := matrix[stableRow][i]
row, column := stableRow, i
// 每个开始元素旋转4次,旋转关系[i][j]-->[j][length-i-1]
for count := 0; count < 4; count++ {
tmp, matrix[column][length-row-1], row, column = matrix[column][length-row-1], tmp, column, length-row-1
}
}
// 开始元素数量减少两个,进入深层递归
interRotateFunc(n + 2)
}
return
}
interRotateFunc(0)
}
原文:https://www.cnblogs.com/gyyyl/p/13668064.html