COCI 2019/2020 CONTEST #1 - Zoo
动物园中有不限数量的两种动物\(T\)与\(B\)
动物园可以看成是\(n\times m\)的一张图,每只动物都会从起点\((1,1)\)开始,在终点\((n,m)\)结束,过程中可能会随机走动
每种动物会在它走过的路径上留下脚印
后一只动物如果走过前一只动物的路径,则后一只动物的脚印会覆盖前一只的脚印
给定一张走完后的图,问这张图表示至少有多少只动物从起点走到终点
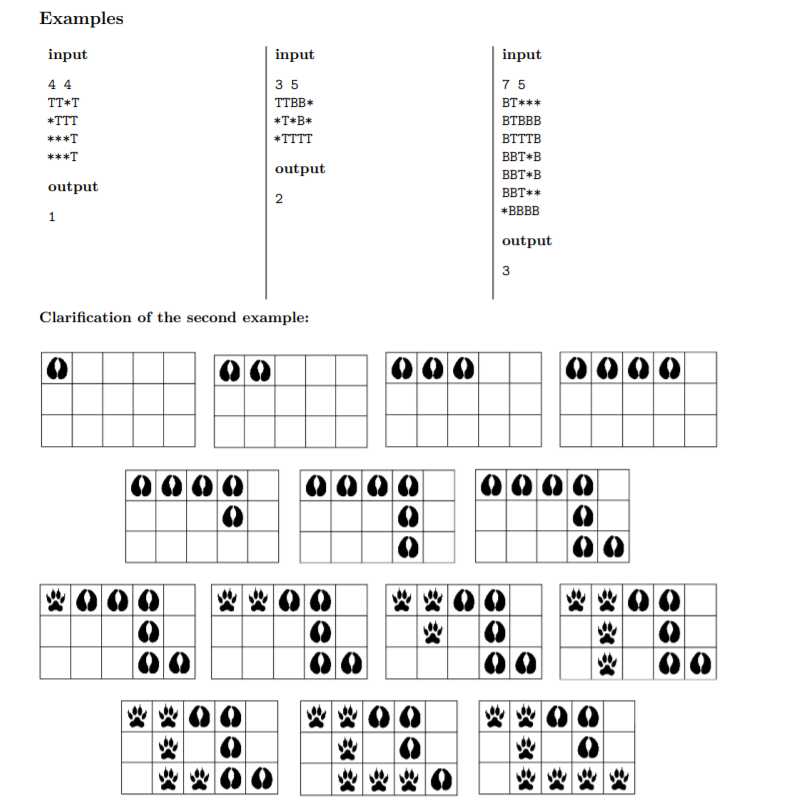
\(2\leq n,m\leq 1000\)
由于每只动物的脚印会覆盖前一只动物的脚印
并且每只动物都会从\((1,1)\)走到\((n,m)\)
那么也就表示每只动物走完后,\((1,1)\)与\((n,m)\)一定在同一连通块中
由于求的是至少有多少只动物
所以可以看成这个连通块代表最后一只动物走过的地点,并且两种动物交替进行
因此对于这张图,可以从最后一只动物开始倒过来推导
每次\((1,1)\)与\((n,m)\)所属连通块都能看成最后一只动物走过的地点
且对于所有动物,这两个点他们一定会经过
所以可以假设后一只动物所走过的地点,前一只动物必定也走过
换言之,除了第一只动物外,后一只动物所走过的点一定是前一只动物走过的点的一部分
那么做法就很明显了,每次从\((1,1)\)搜索相同种类脚印的连通块,并且全部将其翻转成另外一种动物的脚印(\(B\)转\(T\),\(T\)转\(B\))
一直这样循环搜索下去,直到某一次搜索的连通块包含了全图的所有脚印(或者说全图只剩下一种脚印)
那么搜索的次数就表示至少的动物数量,见下方程序一
明显对于上述做法,每次会对当前搜索到的连通块进行翻转,假如所能判断出的动物数量很多,那么翻转的次数将会大大增加(最高时间复杂度大概为\(O(n^4)\))
而对于上面的想法,如果不进行脚印的翻转
可以发现,实际上可以对图进行分层处理
假设刚开始的\((1,1)\)点所在连通块深度为\(1\),那么以独立的相同种类脚印的连通块为一层,通过搜索让整幅图进行分层
那么答案就是脚印深度的最大值

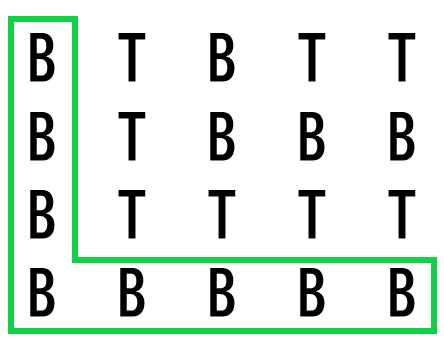

所以直接搜索进行深度计算即可,见下方程序二
如程序二中的写法,借助\(bfs\)来每次判断相邻格子脚印的种类,并根据种类来分类将深度取小
如果种类相同,则深度与“自身”取小
如果种类不同,则深度与“自身+1”取小
明显的,这种方法也可以被一种“环形迷宫”形的样例给卡住,主要是搜索连通块时每次都会根据“是否能够取小”来决定是否进入队列,对于某些点可能会重复进入队列,导致时间复杂度剧增
时间复杂度定高于\(O(n^3)\),接近\(O(n^4)\)
鉴于“可能会重复进入队列”这一点,可以对其专门进行优化
由于我们需要对图进行分层,就能够保证相邻连通块深度差值必为\(1\)
所以每次我们只需要对相同深度的节点进行一次搜索
定义两个队列,交替使用
如果搜索到的某个点种类与当前不一致且“能够取小”,则代表它的深度为当前搜索的连通块深度+1,则放入另外一个队列中
如果搜索到的某个点种类与当前不一致且“不能够取小”,则代表它的深度为当前搜索的连通块深度+1,但已经放入另一个队列中了,无需重复放入
如果搜索到的某个点种类与当前一致且“能够取小”,则代表与当前点属于同一连通块中,放入当前队列
如果搜索到的某个点种类与当前一致且“不能够取小”,则代表与当前点属于同一连通块中,但当前这一遍搜索已经搜索过这个点了,无需重复搜索
根据这四条规则(实际上只要写两条就行),可以将时间复杂度严格控制在\(O(n^2)\)
搜索到两个队列均没有剩余内容为止
#include<bits/stdc++.h>
using namespace std;
typedef pair<int,int> P;
int dx[4]={0,1,0,-1},dy[4]={1,0,-1,0};
int n,m;
char mp[1050][1050];
inline bool prim(int x,int y)
{
return x>0&&y>0&&x<=n&&y<=m;
}
int main()
{
bool flag=false;
int cnt=0;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
{
scanf("%s",mp[i]+1);
for(int j=1;j<=m;j++)
if(mp[i][j]!=‘*‘)
flag=true,cnt++;
}
if(!flag)
{
puts("0");
return 0;
}
int ans=0;
while(true)
{
ans++; //记录搜索次数
queue<P> q;
q.push(P(1,1));
char c=mp[1][1];
mp[1][1]=(mp[1][1]==‘B‘?‘T‘:‘B‘); //翻转(1,1)
int cntd=1;
while(!q.empty())
{
P pd=q.front();
q.pop();
for(int i=0;i<4;i++)
{
int px=pd.first+dx[i],py=pd.second+dy[i];
if(prim(px,py)&&mp[px][py]==c) //相同种类连通块
{
mp[px][py]=mp[1][1]; //连通块内全部翻转
cntd++;
q.push(P(px,py));
}
}
}
if(cnt==cntd) //只剩一个连通块时
break;
}
printf("%d\n",ans);
return 0;
}
#include<bits/stdc++.h>
using namespace std;
typedef pair<int,int> P;
int dx[4]={0,1,0,-1},dy[4]={1,0,-1,0};
int n,m,dep[1050][1050];
char mp[1050][1050];
inline bool prim(int x,int y)
{
return x>0&&y>0&&x<=n&&y<=m;
}
int main()
{
bool flag=false;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
{
scanf("%s",mp[i]+1);
for(int j=1;j<=m;j++)
{
dep[i][j]=0x3f3f3f3f;
if(mp[i][j]!=‘*‘)
flag=true;
}
}
dep[1][1]=1; //起始点深度定作1
if(!flag)
{
puts("0");
return 0;
}
queue<P> q;
q.push(P(1,1));
while(!q.empty())
{
P pd=q.front();
q.pop();
for(int i=0;i<4;i++)
{
int px=pd.first+dx[i],py=pd.second+dy[i];
if(prim(px,py)&&mp[px][py]!=‘*‘)
{
if(mp[px][py]==mp[pd.first][pd.second]&&dep[px][py]>dep[pd.first][pd.second])
{ //如果脚印相同,与深度取小
dep[px][py]=dep[pd.first][pd.second];
q.push(P(px,py));
}
else if(mp[px][py]!=mp[pd.first][pd.second]&&dep[px][py]>dep[pd.first][pd.second]+1)
{ //如果脚印不同,与深度+1取小
dep[px][py]=dep[pd.first][pd.second]+1;
q.push(P(px,py));
}
}
}
}
int ans=1;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
if(mp[i][j]!=‘*‘)
ans=max(ans,dep[i][j]); //找出最大深度作为答案
printf("%d\n",ans);
return 0;
}
#include<bits/stdc++.h>
using namespace std;
typedef pair<int,int> P;
int dx[4]={0,1,0,-1},dy[4]={1,0,-1,0};
int n,m,dep[1050][1050];
char mp[1050][1050];
inline bool prim(int x,int y)
{
return x>0&&y>0&&x<=n&&y<=m;
}
int main()
{
bool flag=false;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
{
scanf("%s",mp[i]+1);
for(int j=1;j<=m;j++)
{
dep[i][j]=0x3f3f3f3f;
if(mp[i][j]!=‘*‘)
flag=true;
}
}
dep[1][1]=1;
if(!flag)
{
puts("0");
return 0;
}
queue<P> q[2];
q[0].push(P(1,1));
int cur=0;
while(!q[cur].empty()) //假如另一队列非空,则将另一队列作为当前队列
{
while(!q[cur].empty()) //假如当前队列非空
{
P pd=q[cur].front();
q[cur].pop();
for(int i=0;i<4;i++)
{
int px=pd.first+dx[i],py=pd.second+dy[i];
if(prim(px,py)&&mp[px][py]!=‘*‘)
{
if(mp[px][py]==mp[pd.first][pd.second]&&dep[px][py]>dep[pd.first][pd.second])
{ //同类且能取小
dep[px][py]=dep[pd.first][pd.second];
q[cur].push(P(px,py)); //放入当前队列
}
else if(mp[px][py]!=mp[pd.first][pd.second]&&dep[px][py]>dep[pd.first][pd.second]+1)
{ //不同类且能取小
dep[px][py]=dep[pd.first][pd.second]+1;
q[cur^1].push(P(px,py)); //放入另一个队列
}
}
}
}
cur^=1; //队列下标切换
}
int ans=1;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
if(mp[i][j]!=‘*‘)
ans=max(ans,dep[i][j]); //取大输出
printf("%d\n",ans);
return 0;
}
原文:https://www.cnblogs.com/stelayuri/p/13670275.html