散列表(Hash table,也叫哈希表),是根据键(Key)而直接访问在内存储存位置的数据结构。它通过计算一个关于键值的函数,将所需查询的数据映射到表中一个位置来访问记录,这加快了查找速度。这个映射函数称做散列函数(Hash Function),存放记录的数组称做散列表。
哈希表工程实践:
顾名思义,我们可以把散列函数定义为hash(key),其中key表示元素的键值,hash(key)的值表示经过散列函数计算得到的散列值。
构成散列函数的基本要求:
实际情况中,想要找到一个不同key对应的散列值都不一样的散列函数几乎是不可能的,再好的散列函数也无法避免散列冲突。常用的散列冲突解决办法有两种,开放寻址法(open addressing)和链表法(chaining)。
开放寻址法的核心思想是,如果出现了散列冲突,我们就重新探测一个空闲位置,将其插入。那如何重新探测新的位置呢?经典探测方法有线性探测(Linear Probing)、二次探测(Quadratic probing)和双重散列(Double hashing)。
不管采用哪种探测方法,当散列表中空闲位置不多的时候,散列冲突的概率就会大大提高。为了尽可能保证散列表的操作效率,一般情况下,我们会尽可能保证散列表中有一定比例的空闲槽位。我们用装载因子(load factor)来表示空位的多少。
装载因子的计算公式是:
散列表的装载因子 = 填入表中的元素个数 / 散列表的长度
往散列表中插入数据时,如果某个数据经过散列函数散列之后,存储位置已经被占用了,我们就从当前位置开始,依次往后查找,看是否有空闲位置,直到找到为止。

白色区域表示空闲位置,绿色区域表示已经存储数据
从图中可以看出,散列表的大小为 10,x 不在散列中时,插入散列表之前,已经有 7 个元素插入到散列表中。x 经过 Hash 算法之后,被散列到位置下标为 7 的位置,但是这个位置已经有数据了,所以就产生了冲突。于是就顺序地往后一个一个找,看有没有空闲的位置,遍历到尾部都没有找到空闲的位置,于是我们再从表头开始找,直到找到空闲位置 3,于是将其插入到这个位置。

在散列表中查找元素的过程类似插入过程。通过散列函数求出要查找元素的键值对应的散列值,然后比较数组中下标为散列值的元素和要查找的元素。如果相等,则说明就是要找的元素;否则就顺序往后依次查找。如果遍历到数组中的空闲位置,还没有找到,就说明要查找的元素并没有在散列表中。
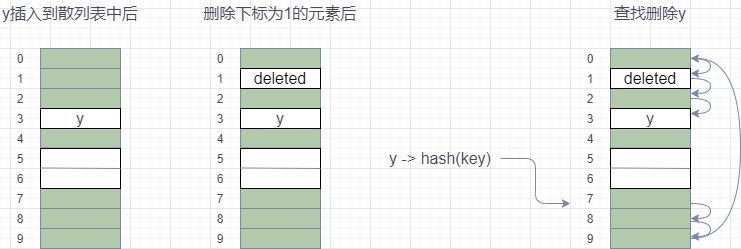
散列表跟数组一样,不仅支持插入、查找操作,还支持删除操作。对于使用线性探测法解决冲突的散列表,删除操作稍微有些特别。删除的元素被特殊标记为 deleted。当线性探测查找的时候,遇到标记为 deleted 的空间,并不是停下来,而是继续往下探测。
所谓二次探测,跟线性探测很像,线性探测每次探测的步长是 1,那它探测的下标序列就是 hash(key)+0,hash(key)+1,hash(key)+2……而二次探测探测的步长就变成了原来的“二次方”,也就是说,它探测的下标序列就是 hash(key)+0,hash(key)+12,hash(key)+22……
所谓双重散列,意思就是不仅要使用一个散列函数。我们使用一组散列函数 hash1(key),hash2(key),hash3(key)……我们先用第一个散列函数,如果计算得到的存储位置已经被占用,再用第二个散列函数,依次类推,直到找到空闲的存储位置。
链表法是一种更加常用的散列冲突解决办法,相比开放寻址法,它要简单很多。我们来看这个图,在散列表中,每个“桶(bucket)”或者“槽(slot)”会对应一条链表,所有散列值相同的元素我们都放到相同槽位对应的链表中。
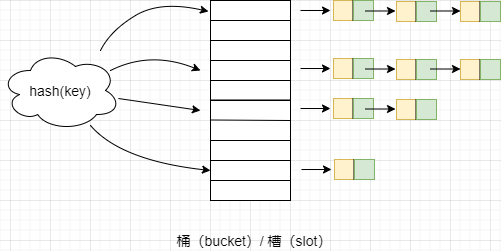
当插入的时候,只需要通过散列函数计算出对应的散列槽位,将其插入到对应链表中即可,所以插入的时间复杂度是O(1)。当查找、删除一个元素时,同样通过散列函数计算出对应的槽,然后遍历链表查找或者删除。查找或删除操作的时间复杂度跟链表的长度 k 成正比,也就是 O(k)。对于散列比较均匀的散列函数来说,理论上讲,k=n/m,其中 n 表示散列中数据的个数,m 表示散列表中“槽”的个数。
给定两个字符串 s 和 t ,编写一个函数来判断 t 是否是 s 的字母异位词。
示例1:
输入: s = "anagram", t = "nagaram"
输出: true
示例 2:
输入: s = "rat", t = "car"
输出: false
说明:
你可以假设字符串只包含小写字母。
进阶:
如果输入字符串包含 unicode 字符怎么办?你能否调整你的解法来应对这种情况?
// 1. 暴力求解 排序 O(nlogn)
public boolean isAnagram(String s, String t) {
if (s.length() != t.length()) {
return false;
}
char[] str1 = s.toCharArray();
char[] str2 = t.toCharArray();
Arrays.sort(str1);
Arrays.sort(str2);
return Arrays.equals(str1, str2);
}
// 2. 哈希表 O(n)
// 用一个计数器表计算 s 字母的频率,用 t 减少计数器表中的每个字母的计数器,然后检查计数器是否回到零
public boolean isAnagram(String s, String t) {
if (s.length() != t.length()) {
return false;
}
int[] counter = new int[26];
for (int i = 0; i < s.length(); i++) {
counter[s.charAt(i) - ‘a‘]++;
counter[t.charAt(i) - ‘a‘]--;
}
for (int count : counter) {
if (count != 0) {
return false;
}
}
return true;
}
给定一个字符串数组,将字母异位词组合在一起。字母异位词指字母相同,但排列不同的字符串。
示例:
输入: ["eat", "tea", "tan", "ate", "nat", "bat"]
输出:
[
["ate","eat","tea"],
["nat","tan"],
["bat"]
]
说明:
所有输入均为小写字母。
不考虑答案输出的顺序。
// 1. 排序数组分类
// 当且仅当它们的排序字符串相等时,两个字符串是字母异位词
// 时间复杂度:O(NKlogK),其中 N 是 strs 的长度,而 K 是 strs 中字符串的最大长度。当我们遍历每个字符串时,外部循环具有的复杂度为 O(N))。然后,我们在O(KlogK) 的时间内对每个字符串排序。
public List<List<String>> groupAnagrams(String[] strs) {
if (strs.length == 0) return new ArrayList();
Map<String, List> ans = new HashMap<String, List>();
for (String s : strs) {
char[] ca = s.toCharArray();
Arrays.sort(ca);
String key = String.valueOf(ca);
if (!ans.containsKey(key)) ans.put(key, new ArrayList());
ans.get(key).add(s);
}
return new ArrayList(ans.values());
}
// 2. 按计数分类
/** 思路:当且仅当它们的字符计数(每个字符的出现次数)相同时,两个字符串是字母异位词
* 算法: 将每个字符串 s 转换为字符数 count,由26个非负整数组成,表示 a,b,c 的数量等。我们使用这些计数作为哈希映射的基础。
* 在 Java 中,我们的字符数 count 的散列化表示将是一个用 **#** 字符分隔的字符串。
* 例如,abbccc 将表示为 #1#2#3#0#0#0 ...#0,其中总共有26个条目。
* 在 python 中,表示将是一个计数的元组。 例如,abbccc 将表示为 (1,2,3,0,0,...,0),其中总共有 26 个条目。
* 时间复杂度: O(NK)
*/
public List<List<String>> groupAnagrams(String[] strs) {
if (strs.length == 0) return new ArrayList();
Map<String, List> ans = new HashMap<String, List>();
int[] count = new int[26];
for (String s : strs) {
Arrays.fill(count, 0);
for (char c : s.toCharArray()) count[c - ‘a‘]++;
StringBuilder sb = new StringBuilder("");
for (int i = 0; i < 26; i++) {
sb.append(‘#‘);
sb.append(count[i]);
}
String key = sb.toString();
if (!ans.containsKey(key)) ans.put(key, new ArrayList());
ans.get(key).add(s);
}
return new ArrayList(ans.values());
}
原文:https://www.cnblogs.com/haif/p/13670274.html