Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 229 Accepted Submission(s): 117
Problem Description
Bit operation is a common computing method in computer science ,Now we have two positive integers A and B ,Please find a positive integer C that minimize the value of the formula (A xor C) & (B xor C) .Sometimes we can find a lot of C to do this ,So you need to find the smallest C that meets the criteria .
For example ,Let‘s say A is equal to 5 and B is equal to 3 ,we can choose C=1,3.... ,so the answer we‘re looking for C is equal to 1.
If the value of the expression is 0 when C=0, please print 1.
Input
The input file contains T test samples.(1<=T<=100)
The first line of input file is an integer T.
Then the T lines contains 2 positive integers, A and B, (1≤A,B<232)
Output
For each test case,you should output the answer and a line for each answer.
Sample Input
1
3 5
Sample Output
1
纪念一下我的傻逼脑子,这个题目肯定是将两个位都是1的消掉,也就是同时异或上a&b ,但是我当时没想到会超int。日,,,wa了多少,还是队友写对的,我真想撞死算了,以后直接longlong,,,,
#include <iostream>
using namespace std;
typedef long long ll ;
int main()
{
int t ;
cin >> t ;
while(t --)
{
ll n , m ;
cin >> n >> m ;
n = 1ll * n & m ;
if(n == 0) n = 1 ;
cout << n << endl ;
}
return 0 ;
}
Problem Description
Heard that eom is a fishing MASTER, you want to acknowledge him as your mentor. As everybody knows, if you want to be a MASTER‘s apprentice, you should pass the trial. So when you find fishing MASTER eom, the trial is as follow:
There are n fish in the pool. For the i - th fish, it takes at least ti minutes to stew(overcook is acceptable). To simplify this problem, the time spent catching a fish is k minutes. You can catch fish one at a time and because there is only one pot, only one fish can be stewed in the pot at a time. While you are catching a fish, you can not put a raw fish you have caught into the pot, that means if you begin to catch a fish, you can‘t stop until after k minutes; when you are not catching fish, you can take a cooked fish (stewed for no less than ti) out of the pot or put a raw fish into the pot, these two operations take no time. Note that if the fish stewed in the pot is not stewed for enough time, you cannot take it out, but you can go to catch another fish or just wait for a while doing nothing until it is sufficiently stewed.
Now eom wants you to catch and stew all the fish as soon as possible (you definitely know that a fish can be eaten only after sufficiently stewed), so that he can have a satisfying meal. If you can complete that in the shortest possible time, eom will accept you as his apprentice and say "I am done! I am full!". If you can‘t, eom will not accept you and say "You are done! You are fool!".
So what‘s the shortest time to pass the trial if you arrange the time optimally?
Input
The first line of input consists of a single integer T(1≤T≤20), denoting the number of test cases.
For each test case, the first line contains two integers n(1≤n≤105),k(1≤k≤109), denoting the number of fish in the pool and the time needed to catch a fish.
the second line contains n integers, t1,t2,…,tn(1≤ti≤109) ,denoting the least time needed to cook the i - th fish.
Output
For each test case, print a single integer in one line, denoting the shortest time to pass the trial.
Sample Input
2
3 5
5 5 8
2 4
3 3
Sample Output
23
11
Hint
Case 1: Catch the 3rd fish (5 mins), put the 3rd fish in, catch the 1st fish (5 mins), wait (3 mins),
take the 3rd fish out, put the 1st fish in, catch the 2nd fish(5 mins),
take the 1st fish out, put the 2nd fish in, wait (5 mins), take the 2nd fish out.
Case 2: Catch the 1st fish (4 mins), put the 1st fish in, catch the 2nd fish (4 mins),
take the 1st fish out, put the 2nd fish in, wait (3 mins), take the 2nd fish out.
这个题目我知道是用贪心做,但是不管怎么想都是错的,根本原因是我没想到可以不止捕一条鱼,我以为在煮鱼的同时只能补一条,也就是即使剩下可以再捕几条鱼的时间也只能捕一条,然后就一直wawawawa的哭啊,
抓第一条鱼的耗时是无法避免的,抓鱼应该从烹饪时间最长的开始抓起,这样才可以用烹饪时间去抓更多的鱼,而剩下的不够抓一条鱼的烹饪时间应该存下来,后面在抓鱼的时候从这些时间中选出最大的x,抓鱼的时间会和烹饪的时间重合最多,这样可以使时间(k-x)最小。
#include <iostream>
#include <queue>
#include <algorithm>
using namespace std;
typedef long long ll ;
priority_queue<int> q ;
const int N = 1e5 + 10 ;
int a[N] ;
bool cmp(int a, int b)
{
return a > b ;
}
int main()
{
int T ;
scanf("%d",&T) ;
while(T --)
{
while(q.size()) q.pop() ;
int n , k ;
scanf("%d%d",&n,&k) ;
for(int i = 1;i <= n;i ++)
scanf("%d" , &a[i]) ;
sort(a + 1 , a + n + 1 , cmp) ;
ll ans = k + a[1] ;
int t = a[1] / k ;
if(a[1] % k)
q.push(a[1] % k) ;
int i ;
for(i = 2;i <= n;i ++)
{
if(t)
{
t -- ;
t += a[i] / k;
ans += a[i] ;
if(a[i] % k)
q.push(a[i] % k) ;
}
else
break ;
}
for(;i <= n;i ++)
{
int x = q.top() ;
q.pop() ;
ans += k - x + a[i] ;
q.push(a[i]) ;
}
cout << ans << endl ;
}
return 0 ;
}
Problem Description
In recent years, CCPC has developed rapidly and gained a large number of competitors .One contestant designed a design called CCPC Windows .The 1-st order CCPC window is shown in the figure:
And the 2-nd order CCPC window is shown in the figure:
We can easily find that the window of CCPC of order k is generated by taking the window of CCPC of order k?1 as C of order k, and the result of inverting C/P in the window of CCPC of order k?1 as P of order k.
And now I have an order k ,please output k-order CCPC Windows , The CCPC window of order k is a 2k?2k matrix.
Input
The input file contains T test samples.(1<=T<=10)
The first line of input file is an integer T.
Then the T lines contains a positive integers k , (1≤k≤10)
Output
For each test case,you should output the answer .
Sample Input
3
1
2
3
Sample Output
CC
PC
CCCC
PCPC
PPCC
CPPC
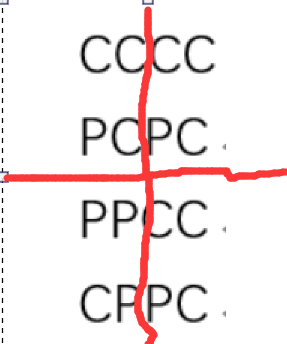
CCCCCCCC
PCPCPCPC
PPCCPPCC
CPPCCPPC
PPPPCCCC
CPCPPCPC
CCPPPPCC
PCCPCPPC
一共要输出2^n行,那么可以一行一行的输出,假设我要输出总行为8行,现在要输出第1行,
那么其实是输出总行为4行的第1行输出两遍,
当输出左下角的部分时,这是总行为4行的相应行相反输出1遍,在输出1遍相同的。
#include <iostream>
#include <algorithm>
#include <cmath>
using namespace std;
void f(int n , int s , int t)
{
if(n == 2)
{
if(t == 1)
{
if(s == 1) cout << "CC" ;
else cout << "PC" ;
}
else
{
if(s == 1) cout << "PP" ;
else cout << "CP" ;
}
return ;
}
int x = s % (n / 2) ;
if(x == 0) x = n / 2 ;
if(t == 1)
{
if(s > n / 2) f(n / 2 , x , 0) ;
else f(n / 2 , x , 1) ;
f(n / 2 , x , 1) ;
}
else if(t == 0)
{
if(s > n / 2)
f(n / 2 , x , 1) ;
else f(n / 2 , x , 0) ;
f(n / 2 , x , 0) ;
}
}
int main()
{
int n , t ;
scanf("%d",&t) ;
while(t --)
{
int n ;
scanf("%d" , &n) ;
n = pow(2 , n) ;
for(int i = 1;i <= n;i ++)
{
f(n , i , 1) ;
puts("") ;
}
}
return 0 ;
}
Problem Description
A deck of card consists of n cards. Each card is different, numbered from 1 to n. At first, the cards were ordered from 1 to n. We complete the shuffle process in the following way, In each operation, we will draw a card and put it in the position of the first card, and repeat this operation for m times.
Please output the order of cards after m operations.
Input
The first line of input contains two positive integers n and m.(1<=n,m<=105)
The second line of the input file has n Numbers, a sequence of 1 through n.
Next there are m rows, each of which has a positive integer si, representing the card number extracted by the i-th operation.
Output
Please output the order of cards after m operations. (There should be one space after each number.)
Sample Input
5 3
1 2 3 4 5
3
4
3
Sample Output
3 4 1 2 5
这个题目说是把每一次操作的牌都放第一位,我踏马,,,,,看错了,这个样例设置的也是够绝,让自己误以为自己写的没错啊,然后直接甩给队友,让他刷水题,一次就AC了 ,,,,
#include <iostream>
using namespace std;
const int N = 1e5 + 10 ;
int a[N] , vis[N] , b[N] , tot , d[N];
int main()
{
int n , m ;
scanf("%d%d",&n,&m);
for(int i = 1;i <= n;i ++)
scanf("%d",&a[i]) ;
for(int i = 1;i <= m;i ++)
scanf("%d",&d[i]) ;
for(int i = m;i >= 1;i --)
if(!vis[d[i]])
b[++ tot] = d[i] , vis[d[i]] = 1 ;
for(int i = 1;i <= n;i ++)
if(!vis[a[i]])
b[++ tot] = a[i] ;
for(int i = 1;i <= tot ;i ++)
printf("%d " , b[i]) ;
return 0 ;
}
上面的四题都是水题,但是我全部栽上面了 ,
Time Limit: 3000/3000 MS (Java/Others) Memory Limit: 524288/524288 K (Java/Others)
Total Submission(s): 2644 Accepted Submission(s): 815
Problem Description
You are given a string S consisting of only lowercase english letters and some queries.
For each query (l,r,k), please output the starting position of the k-th occurence of the substring SlSl+1...Sr in S.
Input
The first line contains an integer T(1≤T≤20), denoting the number of test cases.
The first line of each test case contains two integer N(1≤N≤105),Q(1≤Q≤105), denoting the length of S and the number of queries.
The second line of each test case contains a string S(|S|=N) consisting of only lowercase english letters.
Then Q lines follow, each line contains three integer l,r(1≤l≤r≤N) and k(1≤k≤N), denoting a query.
There are at most 5 testcases which N is greater than 103.
Output
For each query, output the starting position of the k-th occurence of the given substring.
If such position don‘t exists, output ?1 instead.
Sample Input
2
12 6
aaabaabaaaab
3 3 4
2 3 2
7 8 3
3 4 2
1 4 2
8 12 1
1 1
a
1 1 1
Sample Output
5
2
-1
6
9
8
1
(好骚的操作)后缀数组+ st表+二分+主席树
后缀数组,就是将所有后缀按照字典序排序的一个复杂度很低的算法,sa[i]表示第i个小字典序的后缀字符串位置。对于一个字串而言,这个字串肯定是某一个后缀的前缀, 这个整个后缀数组排好序之后,完全符合二分规则,因为字典序已经从小到大弄好了,然后从L开始向左二分一次,向右二分一下,就得到了目标字串的所在sa数组下标区间,::在向左二分的时候,然后如果二分的时候发现这个字串的字典序比mid字典序大了, 那么肯定要往右,因为右边字典序大,否则的话,往左。向右二分的时候反过来。然后此时通过二分得到的sa下标[x , y] , 全部满足suf(sa[i])的前缀都和目标字串相符合,然后在根据主席树求[x , y] , 区间内,sa数组的第k大,即为答案
二分的原理讲解,后缀数组讲解
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <unordered_map>
#include <vector>
#include <map>
#include <list>
#include <queue>
#include <cstring>
#include <cstdlib>
#include <ctime>
#include <cmath>
#include <stack>
#include <set>
#include <bitset>
#include <deque>
#pragma GCC optimize(3 , "Ofast" , "inline")
#pragma GCC optimize("Ofast")
#pragma GCC target("avx,avx2,fma")
#pragma GCC optimization("unroll-loops")
using namespace std ;
#define ios ios::sync_with_stdio(false) , cin.tie(0) , cout.tie(0)
#define x first
#define y second
#define pb push_back
#define ls rt << 1
#define rs rt << 1 | 1
typedef long long ll ;
const double esp = 1e-6 , pi = acos(-1) ;
typedef pair<int , int> PII ;
const int N = 1e6 + 10 , INF = 0x3f3f3f3f , mod = 1e9 + 7;
char s[N];
int n, m;
int y[N], x[N], c[N], sa[N], rk[N], height[N] , st[30][N] ;
int get_SA() {
memset(c, 0, sizeof(c));
for (int i = 1; i <= n; ++i) ++c[x[i] = s[i]];
for (int i = 2; i <= m; ++i) c[i] += c[i - 1];
for (int i = n; i >= 1; --i) sa[c[x[i]]--] = i;
for (int k = 1; k <= n; k <<= 1) {
int num = 0;
for (int i = n - k + 1; i <= n; ++i) y[++num] = i;
for (int i = 1; i <= n; ++i) if (sa[i] > k) y[++num] = sa[i] - k;
for (int i = 1; i <= m; ++i) c[i] = 0;
for (int i = 1; i <= n; ++i) ++c[x[i]];
for (int i = 2; i <= m; ++i) c[i] += c[i - 1];
for (int i = n; i >= 1; --i) sa[c[x[y[i]]]--] = y[i], y[i] = 0;
swap(x, y);
x[sa[1]] = 1;
num = 1;
for (int i = 2; i <= n; ++i)
x[sa[i]] = (y[sa[i]] == y[sa[i - 1]] && y[sa[i] + k] == y[sa[i - 1] + k]) ? num : ++num;
if (num == n) break;
m = num;
}
return 0;
}
int get_height() {
int k = 0;
for (int i = 1; i <= n; ++i) rk[sa[i]] = i;
for (int i = 1; i <= n; ++i) {
if (rk[i] == 1) continue;
if (k) --k;
int j = sa[rk[i] - 1];
while (j + k <= n && i + k <= n && s[i + k] == s[j + k]) ++k;
height[rk[i]] = k;
}
return 0 ;
}
void build_st() {
for (int i = 1; i <= n; i++) st[0][i] = height[i];
for (int k = 1; k <= 19; k++) {
for (int i = 1; i + (1 << k) - 1 <= n; i++) {
st[k][i] = min(st[k - 1][i], st[k - 1][i + (1 << k - 1)]);
}
}
return ;
}
int lcp(int x, int y) {
int l = rk[x], r = rk[y];
if (l > r) swap(l, r);
if (l == r) return n - x + 1;
int t = log2(r - l);
return min(st[t][l + 1], st[t][r - (1 << t) + 1]);
}
struct node {
int l , r , sum ;
}t[N * 4];
int tot = 0 ;
void up(int now) {
t[now].sum = t[t[now].l].sum + t[t[now].r].sum ;
}
void build(int &now , int l , int r) {
t[now = ++ tot].sum = 0 ;
if(l == r) return ;
int mid = l + r >> 1 ;
build(t[now].l , l , mid) ;
build(t[now].r , mid + 1 , r) ;
return ;
}
void update(int &now , int last , int l , int r , int pos) {
t[now = ++ tot] = t[last] ;
t[now].sum ++ ;
if(l == r) return ;
int mid = l + r >> 1 ;
if(pos <= mid) update(t[now].l , t[last].l , l , mid , pos) ;
else update(t[now].r , t[last].r , mid + 1 , r , pos) ;
return ;
}
int ask(int now , int last , int l , int r , int k) {
if(l == r) return l ;
int sum = t[t[now].l].sum - t[t[last].l].sum ;
int mid = l + r>> 1 ;
if(sum >= k) return ask(t[now].l , t[last].l , l , mid , k) ;
else return ask(t[now].r , t[last].r , mid + 1 , r , k - sum) ;
}
int root[N] ;
int work()
{
int q ;
tot = 0 ;
scanf("%d%d" , &n , &q) ;
scanf("%s" , s + 1) ;
m = 123 ;
get_SA() ;
get_height() ;
build_st() ;
build(root[0] , 1, n ) ;
for(int i = 1; i <= n; i ++ ) update(root[i] , root[i - 1] , 1 , n , sa[i]) ;
while(q --) {
int l , r , k ;
scanf("%d%d%d" , &l , &r , &k) ;
int len = r - l + 1 ;
int left = 1 , right = rk[l] ;
int ans = rk[l] ;
while(left <= right) {
int mid = left + right >> 1 ;
if(lcp(sa[mid] , l) >= len) right = mid - 1 , ans = mid ;
else left = mid + 1 ;
}
int LL = ans ;
ans = rk[l] ;
right = n ;
left = rk[l] ;
while(left <= right) {
int mid = left + right >> 1 ;
if(lcp(sa[mid] , l) >= len) left = mid + 1 , ans = mid ;
else right = mid - 1 ;
}
int RR = ans ;
if(RR - LL + 1 < k) puts("-1") ;
else printf("%d\n" , ask(root[RR] , root[LL - 1] , 1 , n , k)) ;
}
return 0 ;
}
int main()
{
// freopen("C://Users//spnooyseed//Desktop//in.txt" , "r" , stdin) ;
// freopen("C://Users//spnooyseed//Desktop//out.txt" , "w" , stdout) ;
int n ;
scanf("%d" , &n) ;
while(n --)
work() ;
return 0 ;
}
/*
*/
原文:https://www.cnblogs.com/spnooyseed/p/13683151.html