蛮力法(brute force)是一种简单直接地解决问题的方法,常常基于问题的描述和所设计的概念定义。
虽然巧妙和高效的算法很少来自于蛮力法,但它在算法设计策略中仍然具有重要地位。
蛮力法适应能力强,是唯一一种几乎什么问题都能解决的一般性方法。
蛮力法一般容易实现,在问题规模不大的情况下,蛮力法能够快速给出一种可接受速度下的求解方法.
虽然通常情况下蛮力法效率很低,但可以作为衡量同类问题更高效算法的准绳。
考虑蛮力法在排序问题中的应用:给定一个可排序的n元素序列,将他们按照非降序方式重新排列。这里讨论两个算法——选择排序和冒泡排序——似乎是两个主要的候选者。
选择排序开始的时候,扫描整个列表,找到它的最小元素然后和第一个元素交换,将最小元素放到它在有序表中的最终位置上。然后我们从第二个元素开始扫描列表,找到最后n-1个元素中的最小元素,再和第二个元素交换位置,把第二小的元素放到它在有序表中的最终位置上。一般来说,在对该列表做第 i 遍扫描的时候(i 的值从0到n-2),该算法在最后n-1个元素中寻找最小元素,然后拿它和A[i]交换。
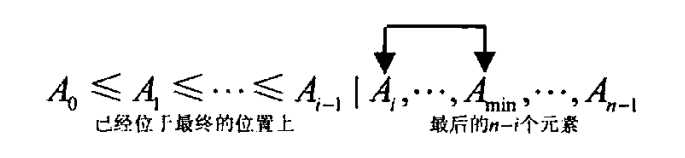
在n-1遍以后,该列表就被排好序了。
下面是算法的伪代码

import java.util.Arrays;
/**
* 选择排序
*/
public class SelectionSort {
/**
* 选择排序
*
* @param arr 待排序的数组
* @return toString输出
*/
public static String selectionSort(Integer[] arr) {
for (int i = 0; i < arr.length; i++) {
// 初始化最小的索引
int minIndex = i;
for (int j = i; j < arr.length; j++) {
// 找到当前的i之后最小数,并记录最小数的索引
if (arr[j] < arr[minIndex]) {
minIndex = j;
}
}
// 交换符合条件的数
int temp = arr[i];
arr[i] = arr[minIndex];
arr[minIndex] = temp;
}
return Arrays.deepToString(arr);
}
public static void main(String[] args) {
Integer[] arr = { 89, 45, 68, 90, 29, 34, 17 };
System.out.println(selectionSort(arr));
}
}
蛮力法在排序问题上还有另一个应用,它比较表中的相邻元素,如果它们是逆序的话就交换他们的位置。重复多次以后,最终,最大的元素“沉到”列表的最后一个位置,第二遍操作将第二大的元素沉下去。这样一直做,直到n-1遍以后,列表就排好序了。
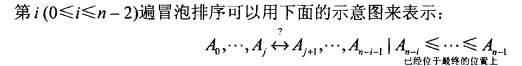
下面是算法的伪代码

Java实现:
import java.util.Arrays;
public class BubbleSort {
/**
* 冒泡排序
*
* @param arr 待排序数组
*/
public static void bubbleSort(int[] arr) {
// 冒泡趟数,n-1趟
for (int i = 0; i < arr.length - 1; i++) {
for (int j = 0; j < arr.length - i - 1; j++) {
if (arr[j + 1] < arr[j]) {
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
}
public static void main(String[] args) {
int[] arr = new int[] { 89, 45, 68, 90, 29, 34, 17 };
bubbleSort(arr);
System.out.println(Arrays.toString(arr));
}
}
作为一个例子,图3.2给出了该算法对于序列89,45,68,90,29,34,17所作操作

我们在前一节中看到了蛮力法在排序问题上的两个应用,这里我们讨论该策略在查找问题中的两个应用。第一个应用处理一个经典的问题,即如何在一个给定的列表中查找一个给定的值。第二个应用则处理字符串匹配问题
顺序查找只是简单地将给定列表中的连续元素和给定的查找键进行比较,直到遇到一个匹配的元素,或者在遇到匹配元素前就遍历了整个列表,也就是查找失败了。

import java.util.stream.IntStream;
public class SequentialSearch {
/**
* 顺序查找
*
* @param a 被查询的数组
* @param key 要查找的key
* @return key所在索引
*/
public static int select(int[] a, int key) {
return IntStream.range(0, a.length)
.filter(i -> a[i] == key)
.findFirst()
.orElse(-1);
}
public static void main(String[] args) {
int[] a = {1, 2, 3, 2, 4, 3, 4, 4, 5};
int key = 5;
select(a, key);
System.out.print(select(a, key));
}
}
如果已知给定的数组是有序的。我们可以对该算法做另外一个简单的改进:在这种列表中,只要遇到一个大于或者等于查找键的元素,查找就可以停止了。
顺序查找是阐释蛮力法的很好的工具,他有蛮力法典型的有点(简单)和缺点(效率低)。
给定一个n个字符组成的串[称为文本(text)],一个m(m≤n)个字符的串[称为模式(pattern)],从文本中寻找匹配模式的字串,更精确的说,我们球的是i——文本中第一个匹配字串最左元素的下标——使得ti = p0, ..., ti+j = pj, ..., ti+m-1 = pm-1
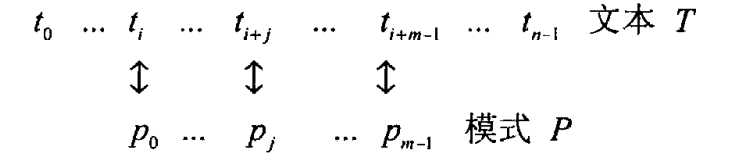
如果还需要寻找另一个匹配子串,字符串匹配算法可以继续工作,直到搜索完全部文本。
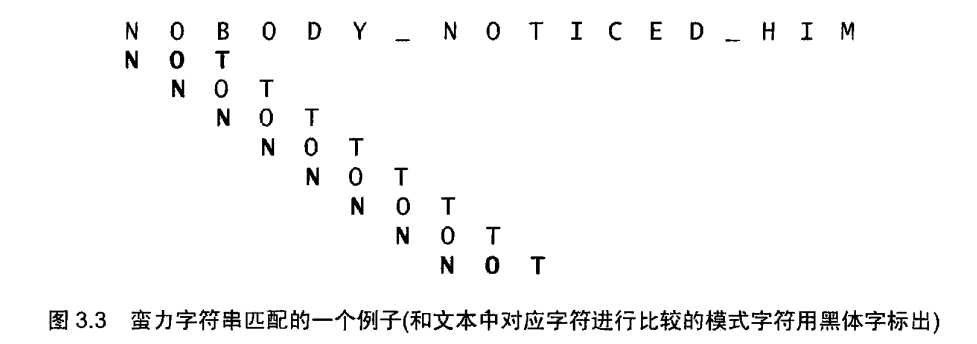
字符串匹配问题的蛮力算法是显而易见的:将模式对准文本的前m个字符,然后从左到右匹配每一对相应的字符,直到m对字符串全部匹配(算法就可以停止了)或者遇到一对不匹配的字符。在后一种情况下,模式向右移一位,然后从模式的第一个字符开始,继续把模式和文本中的对应字符进行比较,请注意,在文本总,最又一轮字串匹配的起始位置是n-m(假设文本位置的下表是从0到n-1)。在这个位置以后,再也没有足够的字符可以匹配整个模式了,因此,该算法也就没有必要在做比较了。

/**
* BF模式匹配算法
*/
public class BruteForceStringMatch {
public static void main(String[] args) {
String src = "NOBODY_NOTTICED_HIM";
String sub = "NOT";
int index = bruteForce(src, sub);
System.out.printf("%s在%s的位置是%d%n", sub, src, index);
}
/**
* BF算法
*
* @param src 主串
* @param sub 模式串
* @return 模式在主串所在索引
*/
public static int bruteForce(String src, String sub) {
int i = 0, j = 0;
while (i < src.length() && j < sub.length()) {
// 如果当前的字符匹配,则主串和模式串继续向后移动
if (src.charAt(i) == sub.charAt(j)) {
i++;
j++;
} else {
// 如果不相同,则主串的指针后移一个,模式串的指针恢复到最开始的位置
i = i - j + 1;
j = 0;
}
}
if (j >= sub.length()) {
// 如果匹配大于等于被匹配字符串长度,说明匹配成功
return i - sub.length();
} else {
return Integer.MIN_VALUE;
}
}
}
本节中,我们考虑两个著名问题的简单解法,这两个问题处理都是平面上的有限点集合。他们除了具有理论上的意义意外,还分别来自于两个重要领域:计算机和和运筹学
最近对问题要求在一个包含n个点的集合,找出距离最近的两个点。
为了简单起见,我们只考虑最近对问题的二维版本。假设所讨论的点都是以标准笛卡尔坐标形式(x,y)给出的,两个点\(p_i=(x_i,y_i)\)和\(p_j=(x_j,y_j)\)之间的距离是标准欧几里得距离。
很显然,求解该问题的蛮力算法应该是这样:分别计算每一对点之间的距离,然后找出距离最小的那一对。当然,我们不希望对同一对点计算两次距离。为了避免这种状况,我们只考虑i<j的那些对\((p_i,p_j)\)。
以下伪代码可以计算两个最近点的距离。如果需要得到最近点对是那两个,则需要对伪代码做一点小小的修改。

import java.util.Arrays;
import java.util.List;
/**
* BruteForceClosestPoints
*/
public class BruteForceClosestPoints {
public static void main(String[] args) {
List<Point> points = Arrays.asList(new Point(1, 1), new Point(1, 9), new Point(2, 5), new Point(3, 1),
new Point(4, 4), new Point(5, 8), new Point(6, 2));
double distance = bruteForceClosestPoints(points);
System.out.printf("最近距离为:%s%n", distance);
}
/**
* 最近点对问题蛮力法
*
* @param points 点list
* @return 最近距离
*/
public static double bruteForceClosestPoints(List<Point> points) {
double dist, minDist = Double.MAX_VALUE;
int size = points.size();
Point p1 = new Point();
Point p2 = new Point();
for (int i = 0; i < size; i++) {
for (int j = i + 1; j < size; j++) {
dist = Math.sqrt(Math.pow(points.get(i).getX() - points.get(j).getX(), 2)
+ Math.pow(points.get(i).getY() - points.get(j).getY(), 2));
if (dist < minDist) {
minDist = dist;
p1 = points.get(i);
p2 = points.get(j);
}
}
}
System.out.printf("最近点对为:%s, %s%n", p1, p2);
return minDist;
}
}
/**
* 点
*/
class Point {
/**
* 横坐标
*/
private double x = Integer.MIN_VALUE;
/**
* 纵坐标
*/
private double y = Integer.MIN_VALUE;
public Point() {
}
public Point(int x, int y) {
this.x = x;
this.y = y;
}
public int getX() {
return x;
}
public void setX(int x) {
this.x = x;
}
public int getY() {
return y;
}
public void setY(int y) {
this.y = y;
}
@Override
public String toString() {
return "Point{" + "x=" + x + ", y=" + y + ‘}‘;
}
}
现在讨论另一个问题——计算凸包。在平面或者高维空间的一个给定点集合中寻找凸包。
先来定义什么是凸集合:
定义对于平面上的一个点集合(有限的或无限的),如果以集合中任意两点p和q为端点的线段都属于该集合,我们说这个集合是凸的。
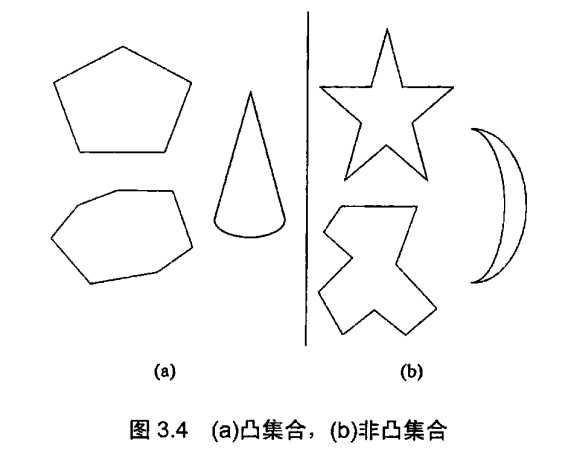
现在可以介绍凸包的概念了,直观地来讲,对于平面上n个点的集合,它的凸包就是包含所有这些点(或者在内部,或者在边界上)的最小凸多边形。如果这个表述还不能激起大家的兴趣,我们可以吧这个问题看作如何用长度最短的栅栏把n头熟睡的老虎围起来。
下面对凸包的正式定义可以应用于任意集合,包括那些正好位于一条直线上的点的集合。
定义一个点的集合S的凸包(convex hull)是包含S的最小凸集合(“最小”意指,S的凸包一定是所有包含S的凸集合的子集)
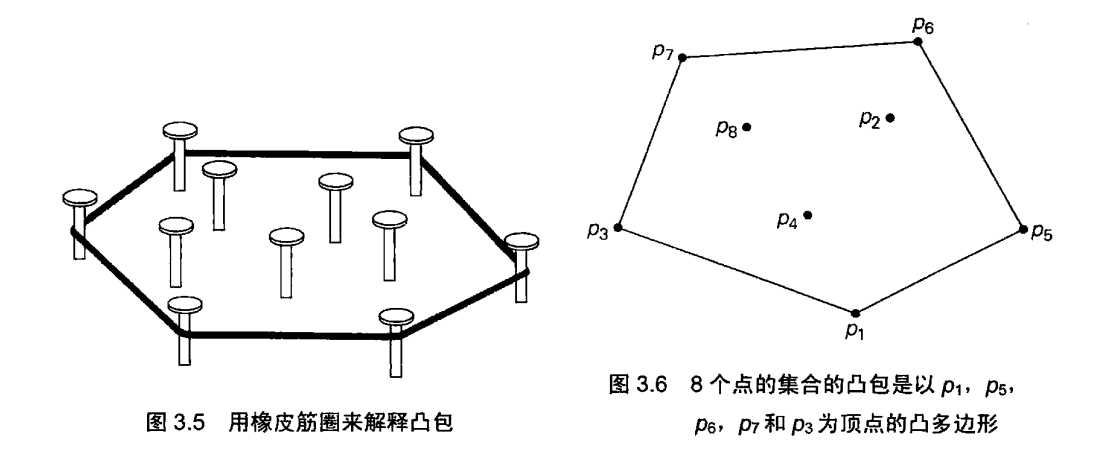
在研究了这个例子以后,下面这个定理其实已经在我们意料之中了
定理 任意包含n>2个点(不共线的点)的集合S的凸包是以S中的某些点为顶点的凸多边形(如果所有的点都位于一条直线上,多边形退化为一条线段,但它的两个端点仍包含在S中)
凸包问题(convex-hull problem)是为一个由n个点的集合构造凸包的问题。为了解决该问题,需要找出某些点,它们将作为这个集合的凸多边形的顶点。数学家将这种多边形的顶点称为“极点”。根据定义,凸集合的极点是这个集合中这样的点:对于任何以集合中的点为端点的线段来说,他们不是这个线段的中点。
极点具有的一些特性是凸集合中的其他点所不具备的。一个称为单纯形法(simplex method)的重要算法利用了其中的一个特性, 10.1节将对此进行讨论。该算法解决的是线性规划(linear programming)问题,这是一种求一个n元线性方程的最大值或最小值的问题(本节习题第12题给出了一个例子,6.6节和10.1节对它做了一般性的讨论),该方程需要满足某些线性约束。然而,这里我们之所以对极点感兴趣,是因为找到了极点,也就解岀了凸
包问题。实际上,为了完全解决该问题,除了知道给定集合中的哪些点是该集合的凸包极点之外,还需要知道另外一些信息:哪几对点需要连接起来以构成凸包的边界。注意,这个问题也可以这样表述:请将极点按照顺时针方向或者逆时针方向排列。
对于一个n个点集合中的两个点p~i~和p~j~,当且仅当该集合中的其他店都位于穿过这两点的直线的通一遍时,他们的连线是该集合凸包边界的一部分,对每一对点都做一遍检验之后,满足条件的线段构成了该凸包的边界。
为了实现一些算法,需要用到一些解析几何的基本知识。首先,在坐标平面上穿过两个点(x~1~, y~1~),(x~2~, y~2~)的直线是有下列方程定义的:
其中,a=y~2~-y~1~,b=x~1~-x~2~,c=x~1~y~2~-y~1~x~2~。
其次,这样一根直线吧平面分为两个半平面:其中一个半平面中的点都满足ax+by>c,而另一个半平面中的点都满足ax+by>c(当然,对于线上的点来说,ax+by=c)。因此,为了检验某些点是否位于这条直线的通一遍,只需要吧每个点带入ax+by-c,检验这个表达式的符号是否相同。
算法的时间复杂度为O(n^3^)。
import java.util.Arrays;
import java.util.stream.IntStream;
public class ConvexHull {
/**
* 蛮力法解决凸包问题
*
* @param points 凸多边形的点数组
* @return 凸多边形的点集合
*/
public static Point[] getConvexPoint(Point[] points) {
Point[] result = new Point[points.length];
// 用于计算最终返回结果中是凸包中点的个数
int len = 0;
for (int i = 0; i < points.length; i++) {
for (int j = 0; j < points.length; j++) {
// 除去选中作为确定直线的第一个点
if (j == i)
continue;
// 存放点到直线距离所使用判断公式的结果
int[] judge = new int[points.length];
for (int k = 0; k < points.length; k++) {
int a = points[j].getY() - points[i].getY();
int b = points[i].getX() - points[j].getX();
int c = (points[i].getX()) * (points[j].getY()) - (points[i].getY()) * (points[j].getX());
// 根据公式计算具体判断结果
judge[k] = a * (points[k].getX()) + b * (points[k].getY()) - c;
}
// 如果点均在直线的一边,则相应的A[i]是凸包中的点
if (judgeArray(judge)) {
result[len++] = points[i];
break;
}
}
}
Point[] result1 = new Point[len];
if (len >= 0) System.arraycopy(result, 0, result1, 0, len);
return result1;
}
/**
* 判断数组中元素是否全部大于等于0或者小于等于0
*
* @param array 数组
* @return 是则返回true,否则返回false
*/
public static boolean judgeArray(int[] array) {
boolean judge = Boolean.FALSE;
int len1, len2;
len1 = (int) IntStream.range(0, array.length).filter(i -> array[i] >= 0).count();
len2 = (int) IntStream.range(0, array.length).filter(j -> array[j] <= 0).count();
if (len1 == array.length || len2 == array.length)
judge = true;
return judge;
}
public static void main(String[] args) {
Point[] A = new Point[8];
A[0] = new Point(1, 0);
A[1] = new Point(0, 1);
A[2] = new Point(0, -1);
A[3] = new Point(-1, 0);
A[4] = new Point(2, 0);
A[5] = new Point(0, 2);
A[6] = new Point(0, -2);
A[7] = new Point(-2, 0);
Point[] result = getConvexPoint(A);
System.out.println("集合A中满足凸包的点集为:");
Arrays.stream(result).forEach(System.out::println);
}
}
class Point {
private int x = 0;
private int y = 0;
public Point() {
}
Point(int x, int y) {
this.x = x;
this.y = y;
}
public void setX(int x) {
this.x = x;
}
public int getX() {
return x;
}
public void setY(int y) {
this.y = y;
}
public int getY() {
return y;
}
@Override
public String toString() {
return "Point{" +
"x=" + x +
", y=" + y +
‘}‘;
}
}
对于组合问题来说,琼剧查找(exhaustive search)是一种简单的蛮力方法,他要求生成问题域中的每一个元素,选出其中满足问题约束的元素,然后在找出一个期望元素。
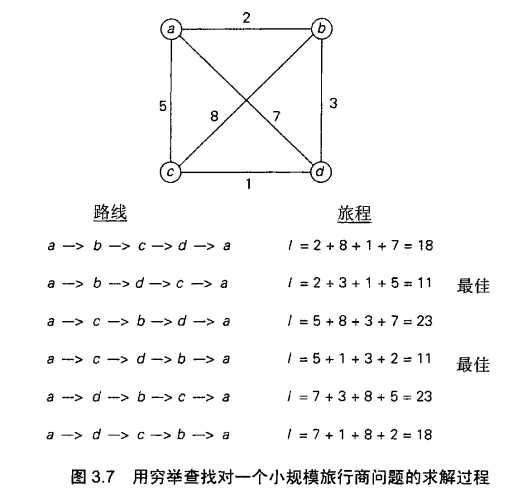
这个问题要求找出一条n个给定城市间的最短路径,使我们在回到出发的城市之前,对每个城市都只访问一次,这个问题可以很方便地用加权图来建模,也就是说,用图的顶点代表城市,用边的权重来表示城市间的距离,这样的问题可就可以表述为求一个图的最短哈密顿回路(Hamiltonian circuit)问题。我们把哈密顿贿赂定义为一个对图的每个顶点都只穿越一次的回路。
很容易看出来,哈密顿回路可以定义为n+1个相邻顶点的一列序列,其中,序列的第一个顶点和最后一个顶点是相同的,而其他的n-1个顶点是互不相同的。因此,可以通过生成n-1个中间城市的组合来得到所有旅行线路,计算这些线路的长度,然后求得最短的线路。
import java.util.Arrays;
import java.util.stream.IntStream;
public class TravelingSalesman {
/**
* 计算当前已行走方案的次数,初始化为0
*/
public static int count = 0;
/**
* 定义完成一个行走方案的最短距离
*/
public static int minDist = Integer.MAX_VALUE;
/**
* 使用二维数组的那个图的路径相关距离长度
*/
public static int[][] distance = { { 0, 2, 5, 7 }, { 2, 0, 8, 3 }, { 5, 8, 0, 1 }, { 7, 3, 1, 0 } };
public static void main(String[] args) {
int[] A = { 0, 1, 2, 3 };
arrange(A, 0, 0, 4, 24); // 此处Max = 4!=24
}
/**
* 旅行商问题
*
* @param arr 图
* @param start 开始进行排序的位置
* @param step 当前正在行走的位置
* @param n 需要排序的总位置数
* @param max n!值
*/
public static void arrange(int[] arr, int start, int step, int n, int max) {
if (step == n) {
count++;
printArray(arr);
}
// n!正好等于是所有的方案个数
if (count == max) {
System.out.println("已完成全部行走方案,最短路径距离为:" + minDist);
} else {
for (int i = start; i < n; i++) {
swapArray(arr, start, i);
arrange(arr, start + 1, step + 1, n, max);
swapArray(arr, i, start);
}
}
}
/**
* 输出数组A的序列,并输出当前行走序列所花距离,并得到已完成的行走方案中最短距离
*
* @param arr 数组
*/
public static void printArray(int[] arr) {
// 输出当前行走方案的序列
Arrays.stream(arr).mapToObj(j -> j + " ").forEachOrdered(System.out::print);
// 此处是因为,最终要返回出发地城市,所以总距离要加上最后到达的城市到出发点城市的距离
int tempDistance = distance[arr[0]][arr[3]];
// 输出当前行走方案所花距离
tempDistance += IntStream.range(0, arr.length - 1).map(i -> distance[arr[i]][arr[i + 1]]).sum();
// 返回当前已完成方案的最短行走距离
if (minDist > tempDistance) {
minDist = tempDistance;
}
System.out.println(" 行走路程总和:" + tempDistance);
}
/**
* 交换数组中两个位置上的数值
*
* @param arr 数组
* @param p 位置p
* @param q 位置q
*/
public static void swapArray(int[] arr, int p, int q) {
int temp = arr[p];
arr[p] = arr[q];
arr[q] = temp;
}
}
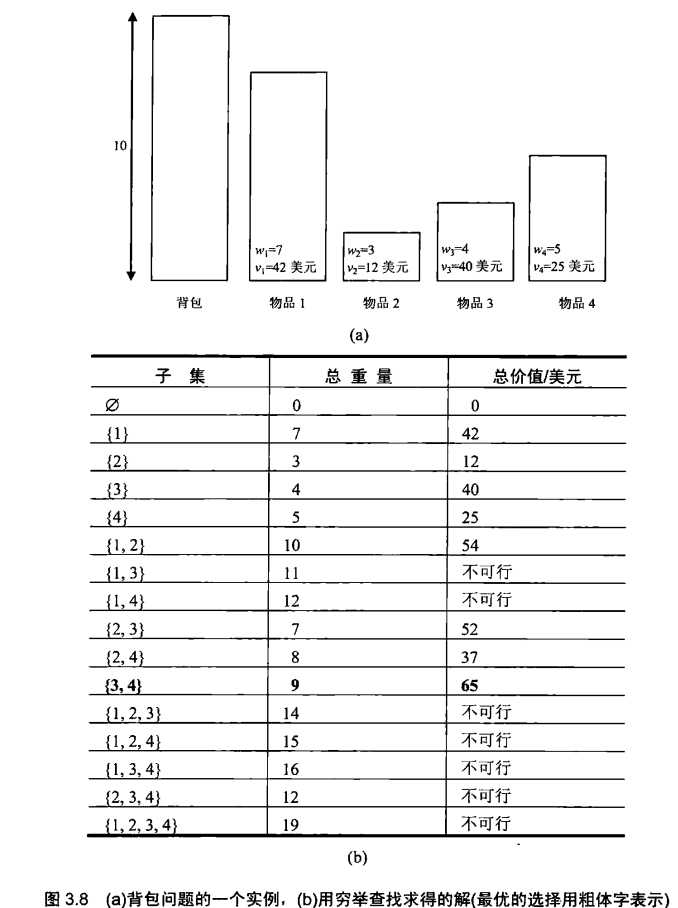
给定n个重量为w~1~,w~2~,...,w~n~,价值为v~1~,v~2~,...,v~n~的物品和一个承重为W的背包,求这些物品中一个最有价值的自己,而且要能够装入背包中。
穷举查找需要考虑给定的n个物品集合的所有子集,复杂度为Ω(2^n^)的算法。
public class BackPack {
public static void main(String[] args) {
int m = 10;
int[] w = {7, 3, 4, 5};
int[] p = {42, 12, 40, 25};
int maxPrice = maxPrice(m, w, p);
System.out.println("maxPrice = " + maxPrice);
}
/**
* 0-1背包问题
*
* @param m 背包总重量
* @param w 物品重量
* @param p 物品价值
* @return 最大价值
*/
public static int maxPrice(int m, int[] w, int[] p) {
// 最大价值,初始化为0
int maxPrice = 0;
// 穷举所有的情况,共2^n中
for (int i = 0; i < Math.pow(2, w.length - 1); i++) {
// 初始化当前的总重量
int weightTotal = 0;
// 初始化当前的总价值
int priceTotal = 0;
// 遍历当前的一种情况,每个物品的情况
for (int j = 0; j < w.length; j++) {
// 当前这种情况下相对应的二进制位上有没有物品
if (get2(i, j) == 1) {
weightTotal += w[j];
priceTotal += p[j];
}
}
if (weightTotal < m && priceTotal >= maxPrice) {
maxPrice = priceTotal;
}
}
return maxPrice;
}
/**
* 当前这种情况下相对应的二进制位上有没有物品,只要result为0,就表示不要,否则表示要这个物品
*
* @param a 遍历到哪一种情况
* @param b 这种情况下的第b个物品要不要算进去
* @return 1表示要,0表示不要
*/
public static int get2(int a, int b) {
int result = a & Double.valueOf(Math.pow(2, b - 1)).intValue();
return result == 0 ? 0 : 1;
}
}
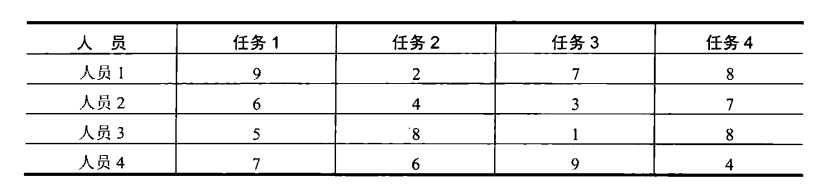
有n个任务需要分配给n个人执行,一个任务对应一个人(意思是说,每个任务只分配给一个人,每个人只分配一个任务),对于每一对i,j=1,2,...,n来说,将第j个任务分配给第i个人的成本是C[i,j]。该问题要找出总成本最小的分配方案。
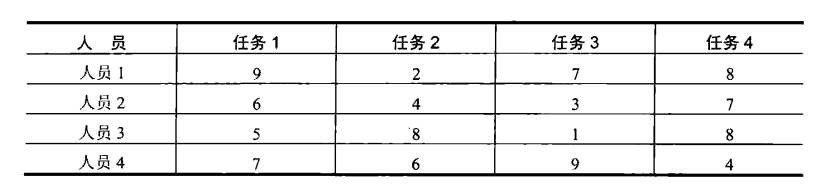
很容易发现,分配问题的实例完全可以用成本矩阵C来表示,就这个矩阵来说,这个问题要求在矩阵的每一行中选出一个元素,这些元素分别属于不同的列,而且元素的和是最小的。

我们可以用一个n维元组<j~1~,...,j~n~>来描述分配问题的一个可能的解,其中第i个分量(i=1,…,n)表示的是在第i行中选择的列号(也就是说,给第i个人分配的任务号)。例如,对于上面的成本矩阵来说,<2,3,4,1>表示这样一种可行的分配:任务2分配给人员1,任务3分配给人员2,任务4分配给人员3,任务1分配给人员4。分配问题的要求意味着,在可行的分配和前n个整数的排列之间存在着一一对应关系。因此,分配问题的穷举查找要求生成整数1,2,….n的全部排列,然后把成本矩阵中的相应元素相加来求得每种分配方案的总成本,最后选出其中具有最小和的方案。如果对上面的实例应用该算法,它的最初几次循环显示在图3.9中。
由于分配问题的一般情况下,需要考虑的排列数了是n!,所以除了该问题的一些规模非常小的实例,穷举查找发几乎是不适用的。幸运的是,对于该问题有一个效率高得多的算法,称为匈牙利方法(Hungarian method)。
深度优先搜索可以从图的任意顶点开始,然后把该顶点标记为已经访问,每次迭代的时候,深度搜索紧接着处理与当前顶点邻接的未访问顶点(如果有若干个顶点,则任意选择一个,也可以按自己的条件选择),让这个过程一直持续,直到遇到一个终点——该点的每个邻接点都被访问过了,然后在该终点上后退一条边,并继续搜索未访问的点,直到返回起点(就是开始搜索的点),直到发现起点的所有邻接点都已经访问过了,此时图的所有联通分量都已经访问过了,如果还有未访问的点,则从此点开始继续上面的过程。
用一个栈来跟踪深度优先查找的操作是比较方便的,在第一次访问一个顶点的时候,我们把该顶点入栈,当他成为要给终点时,我们把它出栈。
在深度优先查找遍历的时候构造一个所谓的深度优先查找森林(depth-first search forest)也是非常有用的。遍历的初始顶点可以作为这样一个森林中的第一棵树的根。无论何时,如果第一次遇到一个新的为访问顶点,它是从哪个顶点被访问到的,就把它附加为那个顶点的孩子。连接这样两个顶点的边称为树向边(tree edge),因为所有这种边的集合构成了一个森林。该算法也可能会遇到一条只想已访问顶点的边,并且这个顶点不是它的直接前驱(即它在树中的父母),我们把这种边称为回边(back edge),因为这条边在一个深度优先查找森林中,把一个顶点和它的非父母祖先连在了一起。
如果要检查一个图中是否包含回路,我们可以利用图的DFS森林形式的表示法。如果DFS森林不包含回边,这个图显然是无回路的。如果从某些节点u到它的祖先v之间有一条回边(例如,在图3.10(c)中从d到a的回边),则该图有一条回路,这个回路是由DFS森林中从v到u的路径上一系列树向边以及从u到v的回边构成的。
DFS一般有两种实现方法:栈和递归
其实递归便是应用了栈的思想,而一般递归的写法非常简单。
以下为伪代码:
public 参数1 DFS(参数2) {
if(返回条件成立) return 参数;
DFS(进行下一步的搜索遍历);
}
先分析if语句:
这句话的作用就是告诉小蛇:是否撞到南墙啦?撞到就返回啦,或者,是否到达终点啦?到了就结束啦!
所以我们在思考使用DFS进行解决问题的时候需要思考这两个问题:
还有一个非常重要的信息:是否需要标记访问节点。
下面来谈谈为什么要标记访问节点,以及如何来标记访问节点。
还是以刚才的路径为例:
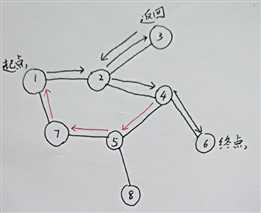
注意当我们的小蛇走到了4号节点时,没有选择去到6号节点,而是去到了5号节点,并沿红色路径行进,这样子是不是很有可能产生一个回环:
1->2->4->5->7->1,你会发现我们的小蛇在疯狂绕圈,肯定是到不了终点6号了。如何才能帮助我们的小蛇呢?
当然是通过标记路径了!
标记路径的原理是什么呢?
小蛇每走过一个节点便标记这个节点为已经访问,小蛇每次需要访问新节点时不会选择已经访问过的节点,这样就避免了出现回环的惨案。
如下图所示,红色的阴影表示已经访问过的节点,小蛇在7号节点时发现1号节点已经访问,所以只好返回,并标记7号节点为以访问。
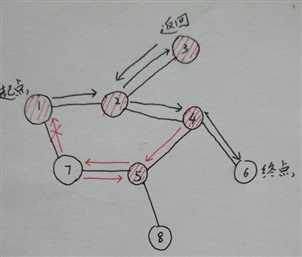
那么如何来标记一个节点是否访问过呢?
有超级多的方法来表示,常见的方法有数组法和HashSet法
// 数组表示,每访问过一个节点,数组将对应元素置为true
boolean[] visited = new boolean[length] ;
// 建立set,每访问一个节点,将该节点加入到set中去
Set<类型> set = new HashSet<>() ;
总结一下,在第一部分,我们要思考3个问题
是否有条件不成立的信息(撞南墙)
是否有条件成立的信息(到终点)
是否需要记录节点(记轨迹)
下面,提一个小问题:如果我要遍历一个图中的所有节点,以上的3个问题如何回答?
答:
所以这个问题的解就是让小蛇没有新节点访问,便完成了整个图的遍历

import java.util.HashMap;
import java.util.LinkedList;
public class DFSDemo {
public static void main(String[] args) {
//构造各顶点
LinkedList<Character> listU = new LinkedList<>();
listU.add(‘v‘);
listU.add(‘x‘);
LinkedList<Character> listV = new LinkedList<>();
listV.add(‘y‘);
LinkedList<Character> listY = new LinkedList<>();
listY.add(‘x‘);
LinkedList<Character> listX = new LinkedList<>();
listX.add(‘v‘);
LinkedList<Character> listW = new LinkedList<>();
listW.add(‘y‘);
listW.add(‘z‘);
LinkedList<Character> listZ = new LinkedList<>();
// 构造图
HashMap<Character, LinkedList<Character>> graph = new HashMap<>();
graph.put(‘u‘, listU);
graph.put(‘v‘, listV);
graph.put(‘y‘, listY);
graph.put(‘x‘, listX);
graph.put(‘w‘, listW);
graph.put(‘z‘, listZ);
HashMap<Character, Boolean> visited = new HashMap<>();
// 调用深度优先遍历方法
dfs(graph, visited);
}
private static void dfs(HashMap<Character, LinkedList<Character>> graph, HashMap<Character, Boolean> visited) {
// 为了和图中的顺序一样,我认为控制了DFS先访问u节点
visit(graph, visited, ‘u‘);
visit(graph, visited, ‘w‘);
}
// 通过一个全局变量count记录了进入每个节点和离开每个节点的时间
static int count;
private static void visit(HashMap<Character, LinkedList<Character>> graph, HashMap<Character, Boolean> visited, char start) {
if (!visited.containsKey(start)) {
count++;
// 记录进入该节点的时间
System.out.println("The time into element " + start + ":" + count);
visited.put(start, true);
for (char c : graph.get(start)) {
if (!visited.containsKey(c)) {
// 递归访问其邻近节点
visit(graph, visited, c);
}
}
count++;
// 记录离开该节点的时间
System.out.println("The time out element " + start + ":" + count);
}
}
}
BFS按照一种同心圆的方式,首先访问所有和初始顶点邻接的顶点,然后是离它两条边的所有未访问顶点,以此类推,知道所有初始顶点同在一个连通分量中的顶点都访问过了位置。如果仍然存在未被访问的顶点,该算法必须从图的其他连通分量中的任意顶点重新开始。
使用队列来跟踪广度优先查找的操作是比较方便的。该队列先从遍历的初始顶点开始,将该顶点标记为已访问,在每次迭代的时候,该算法找出所有和队首顶点领接的未访问顶点,把他们标记为已访问,再把他们入队,然后,将队首顶点从队列中移去。
和DFS遍历类似,在BFS遍历的同时,构造一个所谓的广度优先查找森林(breadth-first search forest)是有意义的。遍历的初始顶点可以作为这样一个森林中第一棵树的根,无论何时,只要第一次遇到一个新的为访问的顶点,它是从哪个顶点被访问到的,就把它附加为哪一个顶点的子女,链接这样两个顶点的边称为树向边。如果一条边只想的是一个曾经访问过的顶点,而且这个顶点不是他的直接前驱,这条边被称为交叉边。
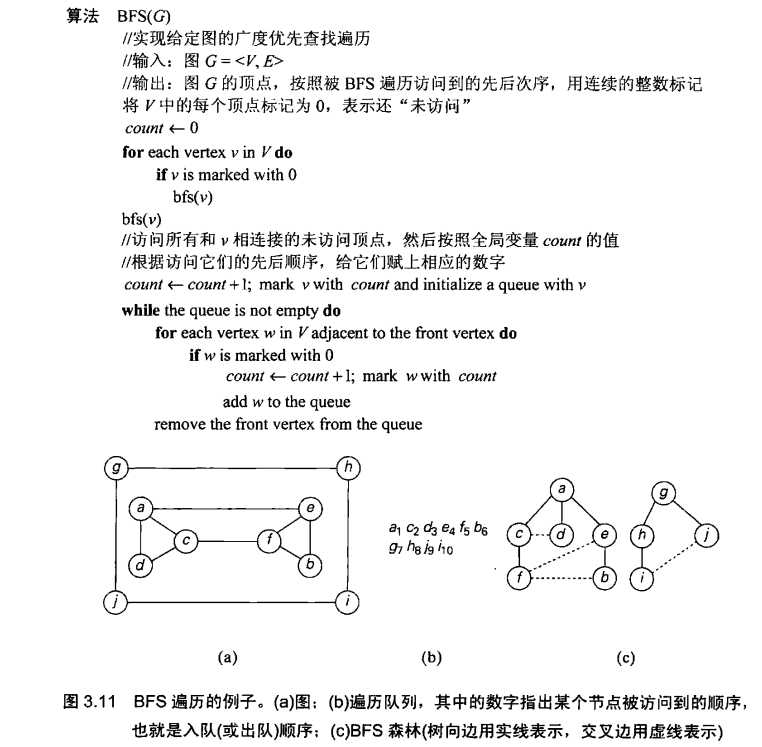
我们也可以用BFS来检查图的连通性和无环性,做法本质上和DFS是一样的。虽然它并不适用于一些较复杂的应用,但却可以用来处理一些DFS无法处理的情况。例如:BFS可以用来求两个给定顶点间边数量最少的路径。我们从两个给定的顶点中开始BFS遍历,一旦访问到了另一个顶点就结束。从BFS树的根到第二个顶点间的最简单路径就是我们所求的路径。
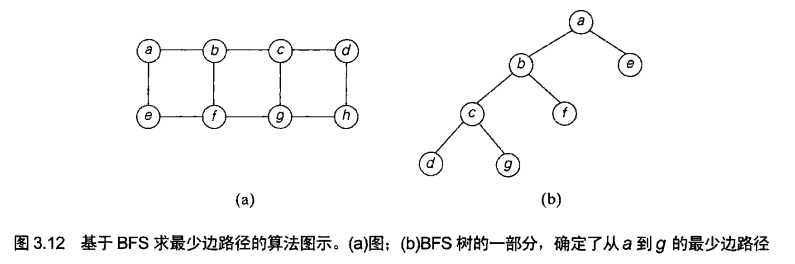
与DFS不同的是,这次不再是每个分叉路口一个一个走了,而是全部,同时遍历,直到找到终点,所对应的“层数”便是最短路径所需要的步数,BFS像是在剥洋葱,一层一层的拨开,最后到达终点。
我们利用队列来实现BFS,伪代码如下:
int BFS(Node root, Node target) {
Queue<Node> queue; // 建立队列
int step = 0; // 建立行动步数
// initialize
add root to queue;
// BFS
while (queue is not empty) {
step = step + 1;
// 记录此时的队列大小
int size = queue.size();
for (int i = 0; i < size; ++i) { //遍历队列中的元素,并将新元素加入到队列中
Node cur = the first node in queue;
return step if cur is target;
for (Node next : the neighbors of cur) {
add next to queue; //加入查找的方向
}
remove the first node from queue;
}
}
return -1; // 没有找到目标返回-1
}
队列整体由两个循环构成:外层循环查看队列是否为空(为空表示元素已经遍历完毕),内层循环用于对当前节点的遍历,以及加入新节点,这里要注意:内层循环的次数size应为queue.size()赋予,而不能直接使用queue.size(),因为在内循环中会对队列进行操作,从而使得队列的长度不停变化。
内层循环代表着一层遍历“一层洋葱皮”,所以在外层遍历与内层遍历直接需要加入步数的记录,最后算法结束时对应步数就是最短路径。

import java.util.HashMap;
import java.util.LinkedList;
import java.util.Queue;
public class BFSDemo {
public static void main(String[] args) {
// 构造各顶点
LinkedList<Character> listS = new LinkedList<>();
listS.add(‘w‘);
listS.add(‘r‘);
LinkedList<Character> listW = new LinkedList<>();
listW.add(‘s‘);
listW.add(‘i‘);
listW.add(‘x‘);
LinkedList<Character> listR = new LinkedList<>();
listR.add(‘s‘);
listR.add(‘v‘);
LinkedList<Character> listX = new LinkedList<>();
listX.add(‘w‘);
listX.add(‘i‘);
listX.add(‘u‘);
listX.add(‘y‘);
LinkedList<Character> listV = new LinkedList<>();
listV.add(‘r‘);
LinkedList<Character> listI = new LinkedList<>();
listI.add(‘u‘);
listI.add(‘x‘);
listI.add(‘w‘);
LinkedList<Character> listU = new LinkedList<>();
listU.add(‘i‘);
listU.add(‘x‘);
listU.add(‘y‘);
LinkedList<Character> listY = new LinkedList<>();
listY.add(‘u‘);
listY.add(‘x‘);
// 构造图
HashMap<Character, LinkedList<Character>> graph = new HashMap<>();
graph.put(‘s‘, listS);
graph.put(‘w‘, listW);
graph.put(‘r‘, listR);
graph.put(‘x‘, listX);
graph.put(‘v‘, listV);
graph.put(‘i‘, listI);
graph.put(‘y‘, listY);
graph.put(‘u‘, listU);
// 记录每个顶点离起始点的距离,也即最短距离
HashMap<Character, Integer> dist = new HashMap<>();
// 遍历的起始点
char start = ‘s‘;
// 调用广度优先方法
bfs(graph, dist, start);
}
private static void bfs(HashMap<Character, LinkedList<Character>> graph, HashMap<Character, Integer> dist, char start) {
Queue<Character> q = new LinkedList<>();
// 将s作为起始顶点加入队列
q.add(start);
dist.put(start, 0);
int i = 0;
while (!q.isEmpty()) {
// 取出队首元素
char top = q.poll();
i++;
System.out.println("The " + i + "th element:" + top + " Distance from s is:" + dist.get(top));
// 得出其周边还未被访问的节点的距离
int d = dist.get(top) + 1;
for (Character c : graph.get(top)) {
// 如果dist中还没有该元素说明还没有被访问
if (!dist.containsKey(c)) {
dist.put(c, d);
q.add(c);
}
}
}
}
}
原文:https://www.cnblogs.com/iamfatotaku/p/13693274.html