正常情况下,每个字或其他可寻址单位(字节、半字等)是作为一个整体数据单元看待的。但是,某些时候还需要将一个n位数据看成由n个1位数据组成,每个取值为0或1。
例如,有时需要存储一个布尔或二进制数据阵列,阵列中的每项只能取值为1或0;有时可能需要提取一个数据项中的某位进行诸如“置位”或“清零"等操作。当数据以这种方式看待
时,就被认为是逻辑数据。因此n位二进制数可表示n个逻辑值。逻辑数据只能参加逻辑运算,并且是按位进行的,如按位“与”按位“或”逻辑左移、逻辑右移等。
逻辑数据和数值数据都是一串0/1序列,在形式上无任何差异,需要通过指令的操作码类型来识别它们。
西文由拉丁字母、数字、标点符号及一些特殊符号所组成,它们统称为字符(character)。所有字符的集合叫做字符集。字符不能直接在计算机内部进行处理,因而也必须对其进行
数字化编码,字符集中每一个字符都有一个代码(即二进制编码的0/1序列),构成了该字符集的代码表,简称码表。码表中的代码具有唯一性。
字符主要用于外部设备和计算机之间交换信息。一旦确定了所使用的字符集和编码方法后,计算机内部所表示的二进制代码和外部设备输入,打印和显示的字符之间就有唯一的对应关系。
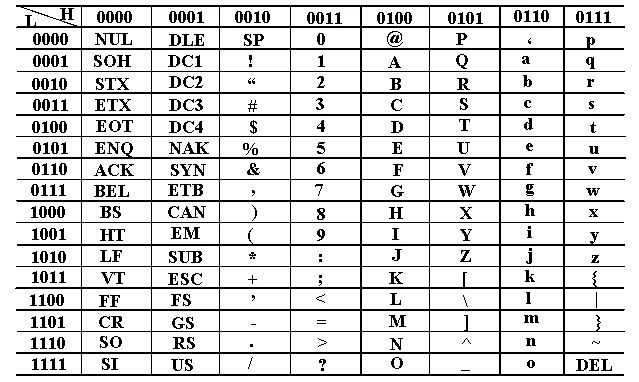
(1)字符0~9这10个数字字符的高3位编码为011,低4位分别为0000~1001。当去掉高3位时﹐低4位正好是0~9这10个数字的8421码。
这样既满足了正常的排序关系,又有利于实现 ASCII码与十进制数之间的转换。
(2)英文字母字符的编码值也满足正常的字母排序关系,而且大,小写字母的编码之间有简单的对应关系,差别仅在b。这一位上,若这一位为0,
则是大写字母;若为1,则是小写字母。这使得大,小写字母之间的转换非常方便。
目前来说,最简便、最广泛采用的汉字输人方法是利用英文键盘输人汉字。由于汉字字数多,无法使每个汉字与西文键盘上的一个键相对应,因此必须使每个汉字用一个或几个键来表示,
这种对每个汉字用相应的按键进行的编码表示就称为汉字的输人码,又称外码。因此汉字的输人码的码元(即组成编码的基本元素)是西文键盘中的某个按键。
汉字被输人到计算机内部后,就按照一种称为内码的编码形式在系统中进行存储、查找,传送等处理。对于西文字符,它的内码就是ASCII码。对于汉字内码的选择,必须考虑以下几个因素:
(1)不能有二义性,即不能和 ASCII 码有相同的编码。
(2)要与汉字在字库中的位置有关系,以便于汉字的处理、查找。
(3)编码应尽量短。
每一个汉字的字形都必须预先存放在计算机内,一套汉字(例如GB2312国标汉字字符集)的所有字符的形状描述信息集合在一起称为字形信息库,简称字库(font)。不同的字
体(如宋体、仿宋、楷体、黑体等)对应不同的字库。在输出每一个汉字时,计算机都要先到字库中去找到它的字形描述信息,然后把字形信息送到相应的设备输出。
汉字的字形主要有两种描述方法:字模点阵描述和轮廓描述。字模点阵描述是将字库中的各个汉字或其他字符的字形(即字模)用一个其元素由0和1组成的方阵(如16×16、
24×24,32×32甚至更大)来表示,汉字或字符中有里占的地方用1表示.空白处用0表示,这种用来描述汉字字模的二进制点阵数据称为汉字的字模点阵码。汉字的轮廓描述方法比
较复杂,它把汉字笔画的轮廓用一组直线和曲线来勾画,记下每一直线和曲线的数学描述公式。目前已有两类国际标准:Adobe Typel和TrueType。这种用轮廓线描述字形的方式精度高,字形大小可以任意变化。
计算机内部任何信息都被表示成二进制编码形式。二进制数据的每一位(0或1)是组成二进制信息的最小单位,称为一个比特(bit),或称位元,简称位。比特是计算机中处理、
存储和传输信息的最小单位。
每个西文字符需要用8个比特表示,而每个汉字需要用16个比特才能表示。在计算机内部,二进制信息的计量单位是字节(byte),也称位组。一个字节等于8个比特。
计算机中运算和处理二进制信息时使用的单位除了比特和字节之外,还经常使用字(word)作为单位。必须注意,不同的计算机,字的长度和组成不完全相同,有的由两个字节
组成,有的由4个、8个甚至16个字节组成。
在考察计算机性能时,一个很重要的性能参数就是机器的字长。平时所说的“某种机器是16位机或是32位机”中的16、32就是指字长。所谓字长通常是指CPU内部用于
整数运算的数据通路的宽度。CPU内部数据通路是指CPU内部的数据流经的路径以及路径上的部件,主要是CPU内部进行数据运算、存储和传送的部件,这些部件的宽度基本
上要一致,才能相互匹配。因此,字长等于CPU内部用于整数运算的运算器位数和通用寄存器宽度。
字和字长的概念不同。字用来表示被处理信息的单位,用来度量各种数据类型的宽度。而字长表示进行数据运算、存储和传送的部件的宽度,它反映了计算机处理信息的一种能力。
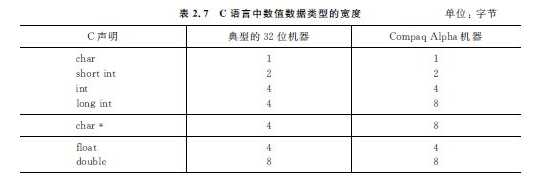
任何信息在计算机中用二进制编码后,得到的都是一串0/1序列,每8位构成一个字节,不同的数据类型具有不同的字节宽度。在计算机中存储数据时,数据从低位到高位可以
按从左到右排列,也可以按从右到左排列。所以,用最左位和最右位来表示数据中的数位时会发生歧义。因此,一般用最低有效位和最高有效位来分别表示数的最低位和最高位。对于带符号
数,最高位是符号位,所以MSB就是符号位。这样,不管数是从左往右排,还是从右往左排,只要明确MSB和LSB的位置,就可以明确数的符号和数值。例如,数5在32位机器上
用int类型表示时的0/1序列为0000 0000 0000 0000 0000:0000 0000 0101,其中最前面的一位0是符号位,即MSB=0,最后面的1是数的最低有效位,即LSB=1.
如果以字节为一个排列基本单位,那么 LSB 表示最低有效字节,MSB 表示最高有效字节.现代计算机基本上都采用字节编址方式,即对存储空间的存储单元进行编号时,每个地址编号中存放一个字节。
在所有计算机中,多字节数据都被存放在连续的字节序列中。根据数据中各字节在连续字节序列中的排列顺序的不同,可有两种排列方式:大端和小端。
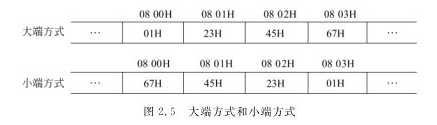
大端方式将数据的最高有效字节MSB存放在低地址单元中,将最低有效字节LSB存放在高地址单元中,即数据的地址就是MSB所在的地址。IBM 360/370、Motorola 68000、
MIPS、SPARC、HP PA等机器都采用大端方式。小端方式将数据的最高有效字节MSB存放在高地址中,将最低有效字节LSB存放在低地址中,即数据的地址就是LSB所在的地址。
数据在计算机内部进行计算、存取和传送过程中,由于元器件故障或噪音干扰等原因会出现差错。为了减少和避免这些错误,一方面要从计算机硬件本身的可靠性入手,在电路、
电源、布线等各方面采取必要的措施,提高计算机的抗干扰能力;另一方面要采取相应的数据检错和校正措施,自动地发现并纠正错误。
目前为止提出的数据校验方法大多采用一种冗余校验的思想,即除原数据信息外,还增加若干位编码,这些新增的代码称为校验位。
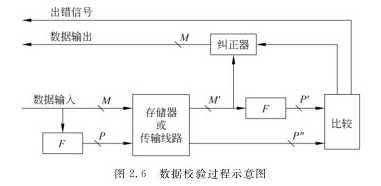
当数据被存入存储器或从源部件传输时,对数据M进行某种运算(用函数F来表示),以产生相应的代码P=F(M),这里P就是校验位。这样原数据信息M和相应的校验位
P一起被存储或传送。当数据被读出或传送到目标部件时,和数据信息一起被存储或传送的校验位也被得到,用于检错和纠错。假定读出后的数据为M‘,通过同样的运算F对M‘也
得到一个新的校验位P‘=F(M‘),假定原来被存储的校验位P取出后其值为P”,将校验位P"与新生成的校验位P‘进行某种比较,根据其比较结果确定是否发生了差错。比较的结果
为以下3种情况之一。
(1)没有检测到错误,得到的数据位直接传送出去。
(2)检测到差错,并可以纠错。数据位和比较结果一起送入纠错器,然后将产生的正确的数据位传送出去。
(3)检测到错误,但无法确认哪位出错,因而不能进行纠错处理,此时,报告出错情况。
为了判断一种码制的冗余程度,并评估它的查错和纠错能力,引入了码距的概念。由若干位代码组成的一个字叫码字,将两个码字逐位比较,具有不同代码的位的个数叫做这两个
码字间的距离,也称为海明距离。一种码制可能有若干个码字,各码字间的最小距离称为码距。例如8421码中,2(0010)和3(0011)之间距离为1,所以8421码制的码距为1,记作d=
1.在数据校验码中,一个码字是指数据位和校验位按照某种规律排列得到的代码。
当码距d≤4时,关系如下:
(1)如果码距d为奇数,则能发现d-1位错,或者能纠正(d-1)/2位错。
(2)如果码距d为偶数,则能发现d/2位错,并能纠正(d/2-1)位错。
最简单的数据校验方法是奇偶校验。实现原理如下:假设将数据B=bn-1bn-2...b1b0从源部件传送至目标部件。在目标部件接收到的数据为B‘=b‘n-1b‘n-2...b1b0.为了判断数据
B在传送中是否发生了错误,可以按照如下步骤来判断。

在奇偶校验码中,若两个数据中有奇数位不同,则它们相应的校验位就不同;若有偶数位不同,则虽校验位相同,但至少有两位数据位不同,因而任意两个码字之间至少有两位不
同,所以码距d=2.根据码距和检错/纠错能力的关系可知,它只能发现奇数位出错,不能发现偶数位出错,而且也不能确定发生错误的位置,不具有纠错能力。但奇偶校验法所用的
开销小,它常被用于存储器读写检查或按字节传输过程中的数据校验。因为一字节长的代码中一位出错的概率相对较大,两位以上出错则很少,所以奇偶校验码用于校验一字节长的
代码还是有效的。
海明校验码主要思想是:将数据按某种规律分成若干组,对每组进行相应的奇偶检测,以提供多位校验信息,从而可对错误位置进行定位,并将其纠正。海明校验码实质上就是一种多重奇偶校验码。
最终比较时按位进行异或操作,根据异或操作的结果,确定是否发生了差错。这种异或操作所得到的结果被称为故障字.显然,校验位和故障字的位数是相同的。
假定被校验数据的位数为n,校验位为k位,则故障字的位数也为k位。那么k位的故障字所能表示的状态最多是2*种,每种状态可用来说明一种出错情况。对于最多只有一位
错的情况,其结果可能是无错,或n位数据中某一位出错,或k位校验码中某一位出错。因此,共有1+n+k种情况,所以,要能对一位错的所有结果进行正确表示,则n和k必须满足
下列关系:2^k≥1+n+k,即 2^k -1≥n+k
数据位和校验位是一起被存储的,通过将它们中的各位按某种方式排列为一个n+k位的码字,将该码字中每一位的出错位置与故障字的数值建立关系,这样就可通过故障字的值
很快确定是该码字中的哪一位发生了错误,从而将其取反来进行纠正。根据上述基本思想,按以下规则来解释各故障字的值:
(1)如果故障字各位全部是0,则表示没有发生错误。
(2)如果故障字中有且仅有一位为1,则表示校验位中有一位出错,不需要纠正。
(3)如果故障字中多位为1,则表示有一个数据位出错,其在码字中的出错位置由故障字的数值来确定。纠正时只要将出错位取反即可。
分组完成后,就可对每组采用相应的奇(偶)校验,以得到相应的一个校验位。假定采用偶校验(即取校验位P1,使对应组中有偶数个1),则得到校验位与数据位之间存在如下关系:
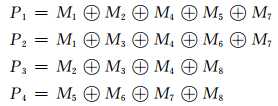
根据上面的公式,可以求出每一组对应的校验位Pi(i=1,2,3,4).数据M和校验位P一起被存储。读出后的数据M通过上述同样的公式得到新的校验位P‘,然后将读出后的校验位
P"与新生成的校验位P‘按位进行异或操作,得到故障字S=S4S3S2S1,根据S的值可以确定是否发生了错误,并且在发生错误时能确定是校验位发生错误还是哪个数据位发生了错误。
看不懂奇偶校验码和海明效验码是怎么操作的,希望可以讲慢点。
原文:https://www.cnblogs.com/2-2OvO/p/13693641.html