某正在实验室砸键盘,叮咚一声,插曲带着小步子来了。群里某位小婊贝问了这样一个问题:0 异或 1 = ? 1 异或 1 = ?某正要轻点键盘展现某花生米大小的智慧时,奈何另一个可耐的小婊贝抢在我前面回答了这个问题:0 异或 1 = 1 1 异或 1 = 0。正当某失望之际,一号小婊贝还举一反三,根据二号小婊贝的解答得到了关于异或的一个重要规律:相同数字异或等于0,不同数字异或等于1。某放下手机,心中未得逞的显摆之心正悄悄流泪。吧唧了一口老茶,摸了摸脑袋上摇摇欲坠的三千万烦恼丝,灵机一动,给大家出了一道题,以发泄被抢风头的”愤怒“:
已知一个数组A[],里面存了n个int类型的整数,但是在这些整数中,只有一个整数出现了一次,其他整数都各自出现了两次,请你设计一个尽量高效的算法,找出此出现一次的整数并返回。(10分)
某放下狠话,请同学们把这个题目看成考试算法题加以解答,并”要求“将答题过程以及代码发到群里,话语态度之绝情尤为可恨。就是要假借考场之名,让大家感受考试的威严,并屈服于这种紧张感之下,从而向某求助,以使某妄图炫耀的邪恶目的得逞。(邪恶^-^)。哪知道!不到一会,另一位小婊贝就把最优方法给出来了,我也只好支支吾吾虚晃一枪,借口一会也会给大家做详细解答,转移大家的注意力。然后,就愤愤然去吃午饭去了。
废话到此,那这个题目如果作为考试代码题,大家应该怎样作答呢?(虽然这样的题目不太可能作为考试代码题)
其实,聪明的小脑袋瓜们肯定立马可以想到一种方法,高呼:这么简单的题目也好意思出?不就是对数组中的每个数,从数组开头开始遍历,直到结尾,遍历结束了如果此数出现了2次那就不是我们想要的值;如果此数出现了1次,那这个数就是我们要求的数,那就返回就行了。二话不说,直接上代码:
1 int fun(int A[],int n){ 2 for(int i=0;i<n;i++){ 3 int count = 0; //定义count表示A[i]元素出现次数 4 for(int j=0;j<n;j++){ 5 if(A[j] == A[i])count++; //发现了和A[i]一样的数,count自增 6 } 7 if(count == 1)return A[i]; //一次循环结束,count的值就是A[i]出现的次数,如果次数为1,那就返回次数,算法结束。 8 } 9 return -1; //因为一定存在出现次数为1的数,所以这个return不会执行,写着只是为了通过编译(因为函数要求有一个返回值) 10 }
恭喜你,没想到你这么快就把这个题目做出来了,某真是佩服万分,并且毫不吝啬地在你的答卷上给了8分这样一个超级高分,再次祝贺。没想到,某的这一声祝贺,招来了百十个臭鸡蛋、AJ鞋底、杨树林口红盒以及诸多骂声:给10分,给10分,不给揍你!
既然大家伙做出了这个题,并且代码正确语法漂亮,那为什么不能给满分呢?其实呀,上面的这种解答被称为”暴力解答“,其特征就是很容易想,但是算法效率可能并不高。聪明的你们肯定立马可以得出此法的时间复杂度:O(n^2)。
那还又没有更快的方法呢?这些就轮到异或登场了,异或确实如开头两位小婊贝所说:相同数字异或等于0,不同数字异或等于1。这种异或被称为可以看成平常意义下的异或(比如十进制的异或)
在计算机中,一般的异或都是按位异或,举个例子:2 异或 1 怎么实现的呢,其实2 和 1 在计算机中都是二进制存储的,所以1在计算机中可能是0001(以4位计算机为例子),2在计算机中就是0010。那么最终的结果其实就是0001、0010对应位异或所得的二进制数:

所以呀,如果两个相同的数按位异或,结果一定是0,比如2 异或 2 如下(这就是小婊贝们的结论相同数字异或等于0。注意,小婊贝们第二个结论:不同数字异或等于0好像和上面 2 异或 1的例子相矛盾,上面的例子照理说应该等于0呀,为什么结果是0011,也就是3呢。不要着急,你回头看看文章开头,一号小婊贝问的问题:0 异或 1 = ? 1 异或 1 = ? 所以呀,这个小婊贝得出的结论不同数字异或等于0,只是针对于单个二进制而言的):
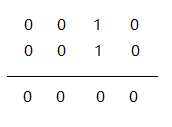
而且还很容易得到两个结论就是:① 0和任何数异或都是等于任何数 ② 异或满足结合律和交换律,即 (a 异或 b) 异或 c 等价于 a 异或 (b 异或 c) a 异或 b 等于 b 异或 a
所以,根据异或的性质,我们就可以立马得到最优解:就是初始化一个t = 0,然后拿着这个t和数组中各个数字异或,然后用异或的结果更新t。在这个过程中,出现两次的数字异或之后等于0,最后只剩下出现一次的数字,t最后的值就是这个数字,返回t即可。代码如下:
1 int fun(int A[],int n){ 2 int t = 0; 3 for(int i=0;i<n;i++){ 4 t ^= A[i]; //^就是按位异或的符号 5 } 6 return t; //最后t就是那个出现一次的数字,返回即可 7 }
你看看,这样一来,就遍历了一次,算法复杂度就是O(n)了,如果你写出了这样的方法,那么恭喜你呀,10分堂而皇之地被你收入囊中。
后记:
这个题其实考试不太可能考到,但是正如我之前所说,它不失为一种发散思维、了解数据结构算法题思考、解答以及给分点的好例子。考试的时候不要害怕,拿到题目立马开始想暴力解法,哪怕最后暴力得到的复杂度比较高,只要能实现功能,那么就可以拿到大部分分,对于大多数人来说,这个分其实完全足够了。如果你平时积累比较多,可以一眼发现最优解法,那么写出来当然很棒,而且也肯定会拿到全分,如果你觉得最优解法比较难想,那么建议老老实实地考虑暴力,暴力并不丢人,而且在时间紧迫的考场上,这反而是一种节省时间的办法。(一般来说,现如今的数据结构算法题,最优解法复杂度一般都不会高于O(n)哦)
但是,对于算法题,也千万不要掉以轻心,认为简单的题目心里会就行了。还必须要实际写到纸上。在写的过程中可以发现很多问题,包括书写啦、思考啦、语法啦等诸多问题,把这些问题都解决了,考试的算法题也就得心应手啦。
最后,祝大家复习顺利哈,拜拜啦
原文:https://www.cnblogs.com/coder-wu/p/13696235.html