1.3 详细代码https://github.com/cantplz/sum
|
PSP2.1 |
Personal Software Process Stages |
预估耗时(分钟) |
实际耗时(分钟) |
|
Planning |
计划 |
20 |
30 |
|
Estimate |
估计这个任务需要多少时间 |
20 |
20 |
|
Development |
开发 |
300 |
450 |
|
Analysis |
需求分析 (包括学习新技术) |
30 |
45 |
|
Design Spec |
生成设计文档 |
30 |
30 |
|
Design Review |
设计复审 (和同事审核设计文档) |
15 |
10 |
|
Coding Standard |
代码规范 (为目前的开发制定合适的规范) |
10 |
10 |
|
Design |
具体设计 |
30 |
35 |
|
Coding |
具体编码 |
60 |
180 |
|
Code Review |
代码复审 |
30 |
20 |
|
Test |
测试(自我测试,修改代码,提交修改) |
40 |
65 |
|
Reporting |
报告 |
85 |
60 |
|
Test Report |
测试报告 |
30 |
25 |
|
Size Measurement |
计算工作量 |
30 |
10 |
|
Postmortem & Process Improvement Plan |
事后总结, 并提出过程改进计划 |
25 |
25 |
|
合计 |
|
347 |
480 |
先由main程序确定要求的算式要求,再由formula程序得出算式
首先,使用随机数生成操作数与运算符,通过参数设置操作数与运算符的数量,再将其拼接为算式,如3×7+9÷3。
其次,在算式上插入括号,括号插在有乘除附近的加减子算式中,如3×(7+9)÷3。
最后,在算式的基础上将其中的数字替换为分数,如果不想使用分数则跳过此步骤。
使用OPT方法存储相关参数,如操作数数值上限、操作数个数、使用的运算符种类、是否包含分数。
使用GeneralFormular类生成算式的中缀表达式,其中包含8个方法。
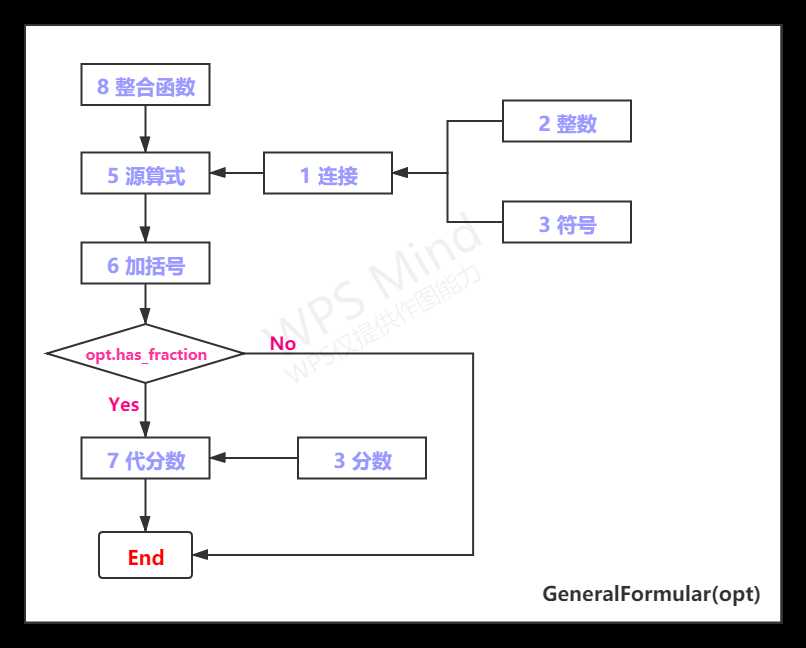
4.代码说明
from formula import OPT, GeneralFormular, ComputeFormular if __name__ == "__main__": print("{:^18} | {:^5} | {:^8}".format("参数", "数值范围", "请输入")) print("{0:-<21}+{0:-<11}+{0:-<12}".format(‘-‘)) n = input("{:>14} | {:9} | ".format("生成算式数量", "[>=1]")) up_limit = input("{:>16} | {:9} | ".format("数值上限", "[>=10]")) oper_num = input("{:>15} | {:9} | ".format("操作数个数", "[>=2]")) oper_variety = input("{:>15} | {:9} | ".format("运算符种数", "[1~4]")) has_fraction = int(input("{:>14} | {:9} | ".format("是否包含分数", "[0, 1]"))) print("{0:-<46}".format(‘-‘)) opt = OPT(up_limit, oper_num, oper_variety, has_fraction) gf = GeneralFormular(opt) cf = ComputeFormular() formulars = {} for i in range(int(n)): f = gf.solve() s = cf.solve(f) formulars[i+1] = f + " = " + s print(formulars[i+1])
5.测试运行

6.性能分析

原文:https://www.cnblogs.com/z2273533704/p/13704883.html