神经网络

神经网络的传播都是形如Y=WX+b的矩阵运算；

为了给矩阵运算加入非线性，需要在隐藏层中加入激活层Relu；

输出层结果需要经过Softmax层处理为概率值;

通过交叉熵损失（Cross Entropy Error）来量化当前网络的优劣。

1.简化的两层神经网络分析

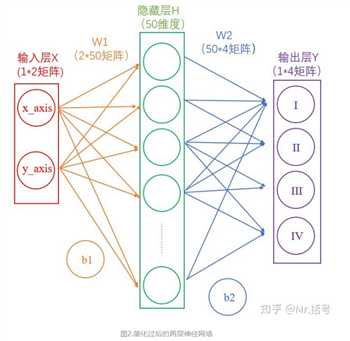
1.2.从输入层到隐藏层

连接输入层和隐藏层的是W1和b1。由X计算得到H十分简单，就是矩阵运算：

（1*50）=（1*2）*（2*50）+（1*50）

在设定隐藏层为50维（也可以理解成50个神经元）之后，矩阵H的大小为（1*50）的矩阵。

1.3.从隐藏层到输出层

连接隐藏层和输出层的是W2和b2。同样是通过矩阵运算进行的：

（1*4）=(1*50)*(50*4)+（1*4）

1.4.分析

一系列线性方程的运算最终都可以用一个线性方程表示。也就是说，上述两个式子联立后可以用一个线性方程表达。

2.激活层:Relu

激活层是为矩阵运算的结果添加非线性的。

常用的激活函数有三种，分别是阶跃函数、Sigmoid和ReLU。

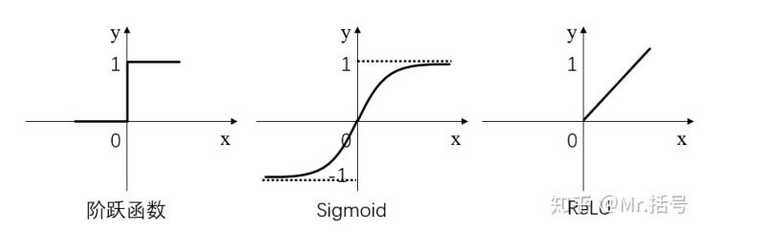
阶跃函数输出值是跳变的，且只有二值，较少使用；

Sigmoid函数在当x的绝对值较大时，曲线的斜率变化很小（梯度消失），并且计算较复杂；

ReLU是当前较为常用的激活函数。

假如经过公式H=X*W1+b1计算得到的H值为：(1,-2,3,-4,7...)，那么经过阶跃函数激活层后就会变为(1,0,1,0,1...)，经过ReLU激活层之后会变为(1,0,3,0,7...)。

每个隐藏层计算（矩阵线性运算）之后，都需要加一层激活层，要不然该层线性计算是没有意义的。

3.输出的正规化:Softmax

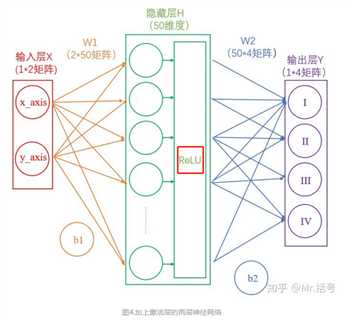
在图4中，输出Y的值可能会是(3,1,0.1,0.5)这样的矩阵，诚然我们可以找到里边的最大值“3”，从而找到对应的分类为I，但是这并不直观。

我们想让最终的输出为概率，也就是说可以生成像(90%,5%,2%,3%)这样的结果，这样做不仅可以找到最大概率的分类，而且可以知道各个分类计算的概率值。

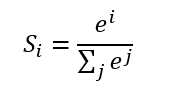
 我们将使用这个计算公式做输出结果正规化处理的层叫做“Softmax”层。此时的神经网络将变成如下图所示：

4.如何衡量输出的好坏:交叉熵损失

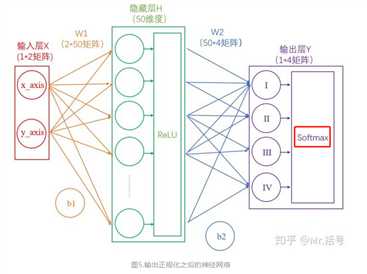
比如，Softmax输出的结果是(90%,5%,3%,2%)，真实的结果是(100%,0,0,0)。虽然输出的结果可以正确分类，但是与真实结果之间是有差距的，一个优秀的网络对结果的预测要无限接近于100%，为此，我们需要将Softmax输出结果的好坏程度做一个“量化”。

一种直观的解决方法，是用1减去Softmax输出的概率，比如1-90%=0.1。不过更为常用且巧妙的方法是，求对数的负数。

还是用90%举例，对数的负数就是：-log0.9=0.046

可以想见，概率越接近100%，该计算结果值越接近于0，说明结果越准确，该输出叫做“交叉熵损失（Cross Entropy Error）”。

我们训练神经网络的目的，就是尽可能地减少这个“交叉熵损失”。

5.反向传播与参数优化

6.迭代

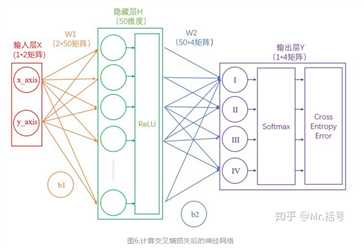
第一次计算得到的概率是90%，交叉熵损失值是0.046；将该损失值反向传播，使W1,b1,W2,b2做相应微调；

再做第二次运算，此时的概率可能就会提高到92%，相应地，损失值也会下降，然后再反向传播损失值，

微调参数W1,b1,W2,b2。依次类推，损失值越来越小，直到我们满意为止。

神经网络

原文：https://www.cnblogs.com/hapyygril/p/13705662.html