统计网站的UV (user view),区别PV (page view)
同一个用户的反复点击进入记为 1 次
解决方案
最简单的思路是记录集合A中所有不重复元素的集合S,当新来一个元素x,若S中不包含元素x,则将x加入S,否则不加入,集合A的基数就是集合S中元素的数量
数据量大时存在的问题
hashmap、set
内存占用大
假设定义
HashMap中Key为string类型,value为boolean。key表示用户的Id,value表示是否点击进入。当百万不同用户访问的时候。此HashMap的内存占用空间为:
100万 * (string + boolean)
B 树
Bitmap 位图
HyperLogLog (HLL)
Redis new data structure: the HyperLogLog(redis 作者博客中所说)
也有说不是一种数据结构,只是一种算法
用来统计一个集合中不重复元素的个数,在不追求绝对准确的情况下,广泛用于大数据场景计算基数
数据集 {1, 3, 5, 7, 5, 7, 8}, 那么这个数据集的基数集为 {1, 3, 5 ,7, 8}, 基数(不重复元素)为5
是一种概率算法,不直接存储数据集合本身,通过一定的概率统计方法预估整体基数值,可以大大节省内存,同时保证误差控制在一定范围内
每个HLL类型的对象只占12KB内存,可以统计2^64个数据的基数。
时间复杂度为O(1)
计数存在一定的误差,误差率整体较低。官方给出的误差率为 0.81%
误差可以被设置辅助计算因子进行降低
是在同样条件下重复地、相互独立地进行的一种随机试验,其特点是该随机试验只有两种可能结果:发生或者不发生。 我们假设该项试验独立重复地进行了n次,那么就称这一系列重复独立的随机试验为n重伯努利试验
二项分布
出现正反面的概率都是1/2,一直抛硬币直到出现正面,记录投掷次数k,这种多次抛硬币直到出现正面的过程就是一次伯努利试验
对于n次伯努利过程,我们会得到n个出现正面的投掷次数值k1,k2……kn,其中最大值记为kmax,那么可以得到下面结论:
对于第一个结论,n次伯努利过程的抛掷次数都不大于kmax的概率用数学公式表示为:
一次过程大于kmax的概率为1/2^kmax,即kmax次都是反面的概率。不大于kmax的概率即1-1/2^kmax
第二个结论,至少有一次等于kmax的概率用数学公式表示为:
一次过程大于kmax-1的概率为1/2^(kmax-1),即kmax-1次都是反面的概率。不大于kmax-1的概率即1-1/2^(kmax-1),大于的概率即1-(1-1/2^(kmax-1))
结合极大似然估算,一顿数学推导,得出在n和k_max中存在估算关系:n = 2^(k_max)
即n次抛硬币试验,记录首次抛到正面的次数k,则可以用2^kmax 估算n的大小
利用已知的样本结果信息,反推最具有可能(最大概率)导致这些样本结果出现的模型参数值
假如有一个罐子,里面有黑白两种颜色的球,数目多少不知,两种颜色的比例也不知。我们想知道罐中白球和黑球的比例,但我们不能把罐中的球全部拿出来数。现在我们可以每次任意从已经摇匀的罐中拿一个球出来,记录球的颜色,然后把拿出来的球再放回罐中。重复这个过程,用记录的球的颜色来估计罐中黑白球的比例。
假如在前面的一百次重复记录中,有七十次是白球,请问罐中白球所占的比例最有可能是多少?(70%)
假设罐中白球的比例是p,那么黑球的比例就是1-p。因为每抽一个球出来,在记录颜色之后,我们把抽出的球放回了罐中并摇匀,所以每次抽出来的球的颜色服从同一独立分布。则题目所描述的事件出现的概率为
P=p^70(1-p)^30。该模型中的参数p最有可能是多少?
随机过程中,任何时刻的取值都为随机变量
例如随机变量X1和X2独立,是指X1的取值不影响X2的取值,X2的取值也不影响X1的取值且随机变量X1和X2服从同一分布,意味着X1和X2具有相同的分布形状和相同的分布参数,对离散随机变量具有相同的分布律,对连续随机变量具有相同的概率密度函数,有着相同的分布函数,相同的期望、方差。
如实验条件保持不变,一系列的抛硬币的正反面结果是独立同分布
我们把一次抽出来球的颜色称为一次抽样。题目中在一百次抽样中,七十次是白球的,三十次为黑球事件的概率为
求出该模型中的参数值p
p可以有很多种取值(分布),不同的取值P的值也不同
p=50% => P=7.88*10^(-31)
p=60% => P=3.40*10^(-28)
p=70% => P=2.95*10^(-27) 最大
p=80% => P=1.76*10^(-28)
p=90% => P=6.26*10^(-34)
极大似然估计按照让这个样本结果出现的可能性最大的原则去选取分布
即 p^70(1-p)^30 最大,导数为0,可得p=70%
p取值范围[0,100]
闭区间[a,b]上连续的函数f(x)在[a,b]上必有最大值与最小值
初等函数(基本函数)是由常函数、幂函数、指数函数、对数函数、三角函数和反三角函数经过有限次的有理运算(加、减、乘、除、有限次乘方、有限次开方)及有限次函数复合所产生、并且在定义域上能用一个方程式表示的函数
初等函数在其定义域内是连续的
统计一组数据中不重复元素的个数,HLL在添加元素时会通过内部的一个hash函数,将其转换为一个长度为64的比特串,这些比特串就类似一次抛硬币的过程(0表示反面,1表示正面)。统计比特串中首次出现1的位置,并以此预估整体基数
如果只有一组试验,恰好第一次过程首次出现正面的次数就是10,,则以此估算试验次数误差很大2^10
如果同时进行100组试验,用每组试验估算出来的值求平均数,则会消减因偶然性带来的误差,提高预估的准确性
HLL 使用了分桶的概念,内部维护了一个长度为2^14(16384)的数组S,每个下标代表一个桶,每个桶占用6bit。
数据经过hash计算得出的64比特串,低14位用来计算桶的位置即数组S中的下标x(从0开始),高50位从右向左计算首次出现1的位置k(从1开始),将k与桶中旧值比较,大于则替换旧值,否则丢弃。在计算基数时,分别计算每个桶中的值,再带入HLL公式中,得出最终估算的基数
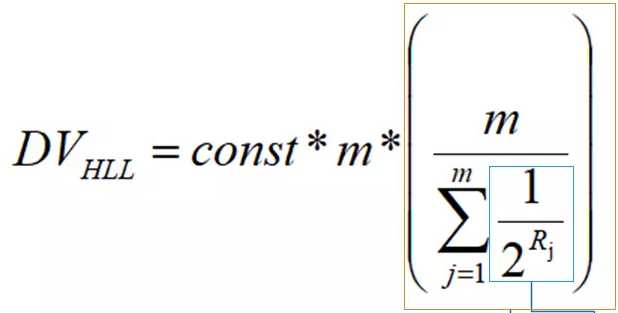
DV(Distinct Value) :基数
m:伯努利试验次数,即桶个数
Rj:表示每个桶的计数值
黄色框中的式子:表示 根据每个桶中的计数值 估算出的整体基数的 调和平均数
调和平均数(harmonic mean)又称倒数平均数,是总体各统计变量倒数的算术平均数的倒数
不容易受极大值的影响,给予较小值更高的权重,强调了较小值的重要性
例如
- 并联电阻
- 一艘轮船从A码头顺流而下到C码头然后原路返回,顺流而下去时速度30千米/时,逆流而上返回20千米/时。求往返平均速度。容易错成(30+20)÷2=25(千米/时),因为往返使用的时间是不同的。事实上结果应该是30和20的调和平均数。2/(1/20+1/30)=2×20×30/(20+30)=24(千米/时)
const(constant): 修正因子,用于校正,具体数值跟桶数目有关
HLL使用一种分阶段修正算法。当HLL算法开始统计数据时,统计数组中大部分位置都是空数据,并且需要一段时间才能填满数组,这种阶段引入一种小范围修正方法;当HLL算法中统计数组已满的时候,需要统计的数据基数很大,这时候hash空间会出现很多碰撞情况,这种阶段引入一种大范围修正方法
m = 2^b #with b in [4...16]
if m == 16:
alpha = 0.673
elif m == 32:
alpha = 0.697
elif m == 64:
alpha = 0.709
else:
alpha = 0.7213/(1 + 1.079/m)
alpha = constant
######
HLL是LL的优化
LL的估算公式

m:伯努利试验次数,即桶个数
const(constant): 修正因子,用于校正,具体数值跟桶数目有关
头上有一横的R是所有桶中数值的算数平均数(k_max_1 + ... + k_max_m)/m。
当统计数据量较小时误差较大
If M(j) is the (random) value of parameter R on bucket number j, then the
arithmetic mean
大端模式,是指数据的高字节保存在内存的低地址中,而数据的低字节保存在内存的高地址中
小端模式,是指数据的高字节保存在内存的高地址中,而数据的低字节保存在内存的低地址中
Intel X86结构是小端模式
0x12345678
0x 16进制,1位16进制对应4位二进制数据,2位16进制占用1字节
内存地址用字节数组buf表示,每个元素代表1字节
大端模式表示为
高地址 -- buf[3] (0x78) -- 低位
buf[2] (0x56)
buf[1] (0x34)
低地址 -- buf[0] (0x12) -- 高位
小端模式表示为
高地址 -- buf[3] (0x12) -- 高位
buf[2] (0x34)
buf[1] (0x56)
低地址 -- buf[0] (0x78) -- 低位
在计算机存储系统以字节为单位,每个地址单元都对应着一个字节,一个字节为 8bit。
编程语言中不同类型的数据占用字节数不同,例如C语言中除了8bit的char之外,还有16bit的short型,32bit的long型(要看具体的编译器)。因此存在对多字节的安排问题,导致了大小端两种不同的存储模式
例如一个16bit的short型x,在内存中的地址为0x0010,x的值为0x1122,那么0x11为高字节,0x22为低字节。对于 大端模式,就将0x11放在低地址中,即0x0010中,0x22放在高地址中,即0x0011中。小端模式,刚好相反
Redis 内部是使用字符串位图来存储 HyperLogLog 所有桶的计数值
使用连续的 16384个桶,组成字符串位图

通过64比特串的后14位计算得出十进制桶编号为idx,如果根据桶编号获取其存储的计数值?
因为一个字节8bit,一个桶6bit,某个桶所占用的地址可能在一个字节内,也可能跨字节
假设桶的编号为idx,其占用地址的起始字节位置偏移用 offset_bytes表示,它在这个字节的起始比特位置偏移用 offset_bits 表示。我们有
offset_bytes = (idx * 6) / 8 取商
offset_bits = (idx * 6) % 8 取余
比如 bucket 2 的字节偏移是 1,也就是第 2 个字节。它的位偏移是4,也就是第 2 个字节的第 5 个位开始是 bucket 2 的计数值。
需要注意的是字节位序是左边低位右边高位(小端模式),而通常我们书写二进制都是左边高位右边低位,因此这里需要倒置
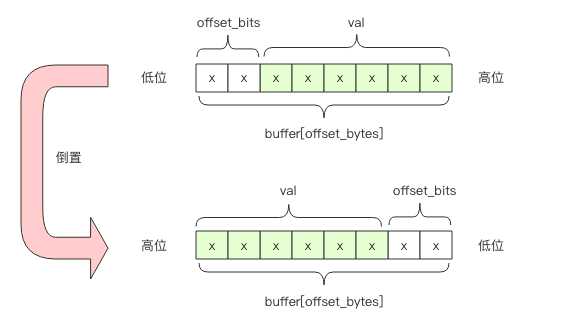
此时,该桶表示的6bit在一个字节内,则表示的计数值为
val = buffer[offset_bytes] >> offset_bits # 向右移位
右移运算符 >>
按二进制形式把所有的数字向右移动对应位移位数,低位移出(舍弃),高位的空位补符号位,即正数补零,负数补1
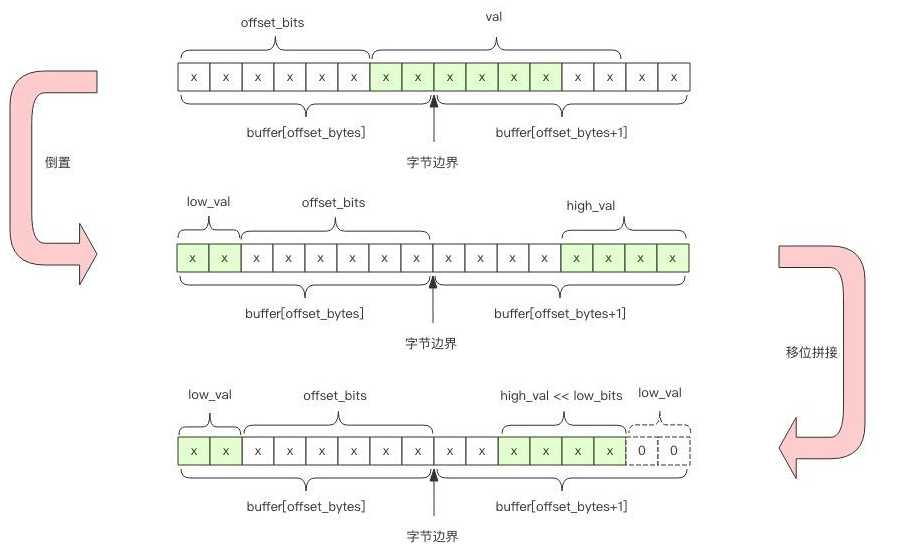
此时该桶表示的6bit跨字节,需要拼接两个字节的位片段
# 低位值
low_val = buffer[offset_bytes] >> offset_bits
# 低位个数
low_bits = 8 - offset_bits
# 拼接,保留低6位
val = (high_val << low_bits | low_val) & 0b111111
按位或 |
0|0=0; 0|1=1; 1|0=1; 1|1=1
按位与 &
0&0=0; 0&1=0; 1&0=0; 1&1=1
#define HLL_DENSE_GET_REGISTER(target,p,regnum) do { uint8_t *_p = (uint8_t*) p; unsigned long _byte = regnum*HLL_BITS/8; \ unsigned long _fb = regnum*HLL_BITS&7; \ # %8 = &7 unsigned long _fb8 = 8 - _fb; unsigned long b0 = _p[_byte]; unsigned long b1 = _p[_byte+1]; target = ((b0 >> _fb) | (b1 << _fb8)) & HLL_REGISTER_MAX; } while(0)
适用于很多计数值都是零的情况

HLL最开始是稀疏存储
当多个连续桶的计数值都是零时,Redis使用一个字节来表示多少个桶的计数值都是零即00xxxxxx,前缀两个零表示接下来的6bit整数值加1就是零值计数器的数量,比如 00010101表示连续 22 个零值计数器;6bit最多能表示连续64个零值计数器,如果大于64个,采用两个个字节表示即01xxxxxx yyyyyyyy,后面的 14bit 可以表示最多连续 16384 个零值计数器。
如果连续几个桶的计数值非零,那就使用形如 1vvvvvxx 这样的一个字节来表示。中间 5bit 表示计数值(最大能表示32),尾部 2bit 表示连续几个桶。它的意思是连续 (xx +1) 个桶的计数值都是 (vvvvv + 1)。比如 10101011 表示连续 4 个计数值都是 11。
注意这两个值都需要加 1,因为任意一个是零都意味着这个计数值为零,那就应该使用零计数值的形式来表示。注意计数值最大只能表示到32,而密集存储单个计数值用 6bit 表示,最大可以表示到 63。当稀疏存储的某个计数值需要调整到大于 32 时,Redis 就会立即转换 HyperLogLog 的存储结构,将稀疏存储转换成密集存储
当某个桶的计数值满足以下条件
稀疏存储将不可逆一次性转换成密集型存储
pfadd
pfadd key value [value...]
127.0.0.1:6379> pfadd pfkey u1 u2
(integer) 1
pfcount
pfcount key [key...]
计算一个或多个 HyperLogLog 的独立总数
如果是多个 HyperLogLog 则返回所有独立总数中的最大值
127.0.0.1:6379> pfadd pfkey u1 u2
(integer) 1
127.0.0.1:6379> pfcount pfkey
(integer) 2127.0.0.1:6379> pfadd pfkey u1 u3
(integer) 1
127.0.0.1:6379> pfcount pfkey
(integer) 3//
127.0.0.1:6379> pfadd pfkey2 u1 u2
(integer) 1127.0.0.1:6379> pfcount pfkey2
(integer) 2127.0.0.1:6379> pfcount pfkey pfkey2
(integer) 3 // 返回3
pfmerge
pfmerge destKey sourceKey [sourceKey...]
求多个HyperLogLog的并集并赋值给 destKey
返回多个HyperLogLog的并集
127.0.0.1:6379> pfadd pfkey2 u1 u2
(integer) 1127.0.0.1:6379> pfadd pfkey3 u1 u2 u3 u3 u4
(integer) 1
127.0.0.1:6379> pfmerge pfkey0 pfkey2 pfkey3
OK127.0.0.1:6379> pfcount pfkey0
(integer) 4
所用命令以pf开头,致敬HLL算法的发明者 Philippe Flajolet
统计某个网站的UV
用户搜索网站的关键词数量
数据分析
网络监控
数据库优化
HLL 中用2^14(16384)个桶,每个桶占6bit,占用内存为
java中long 类型占用8个字节64bit,最大值为 2^63-1,那么 2^63-1 个long类型的数据,占用内存为
long 64 位、有符号整数,数值范围 (-2^63~2^63-1)
//用HyperLogLog类型测试
插入之前
used_memory:604488 byte
used_memory_human:590.32K(604488 / 1024)
插入之后
used_memory:618872
used_memory_human:604.37K 增加 14KB
//用set类型测试
插入之前
used_memory:618872
used_memory_human:604.37K
插入之后
used_memory:3929664
used_memory_human:3.75M(3837.56K) 增加 3.16M
127.0.0.1:6379> pfcount test2
(integer) 49650 // 误差率 50000-49650=350 350/50000=0.007 => 0.7%
127.0.0.1:6379> scard test3
(integer) 50000
//用HyperLogLog类型测试
插入之前
used_memory:3143640
used_memory_human:3.00M
插入之后
used_memory:3158024 增加14384 byte
used_memory_human:3.01M 增加 14KB
127.0.0.1:6379> pfcount pf1
(integer) 1000110 // 误差率 110/1000000=0.00011 => 0.011%
//set 类型测试
插入之前
used_memory:3158024
used_memory_human:3.01M
插入之后
used_memory:51546704
used_memory_human:49.16M 增加 46.15M
127.0.0.1:6379> scard pf2
(integer) 1000000
原文:https://www.cnblogs.com/usmile/p/13709293.html