①.记忆
②.钱包-储物柜
③.代码模块
一个经典的链表应用场景,那就是 LRU 缓存淘汰算法。
缓存是一种提高数据读取性能的技术,在硬件设计、软件开发中都有着非常广泛的应用,比如常见的 CPU 缓存、数据库缓存、浏览器缓存等等。
缓存的大小有限,当缓存被用满时,哪些数据应该被清理出去,哪些数据应该被保留?这就需要缓存淘汰策略来决定。
常见的策略有三种:
打个比方说,你买了很多本技术书,但发现这些书太多,太占书房空间,需要个大扫除,扔掉一些书籍。你会选择扔掉哪些书呢?对应一下,你的选择标准是不是和上面的三种策略神似。
Understanding the Meltdown exploit – in my own simple words
上图为四核CPU,三级缓存(L1 Cache,L2 Cache ,L3 Cache);
每一个核里边就有L1 D-Cache,L1 l-Cache,L2 Cache,L3 Cache;最常用的数据马上要给CPU的计算模块进行计算处理的就放在L1里边,次之不常用的就放在L1 l-Cache里边,再次之放在L2Cache里边,最后放在L3 Cache里边。外边即内存。他们的速度 L1 D-Cache > L1 l-Cache > L2-Cache > L3-Cache
体积(能存的数据多少)即 L1 D-Cache < L1 l-Cache < L2-Cache < L3-Cache
两个要素:
大小
替换策略(least recent use -- 最近最少使用)
实现机制:
HashTable+DoubleLinkedList
复杂度分析:
O(1)查询
O(1)修改、 更新
LRU Cache工作示例:
更新原则 least recent use
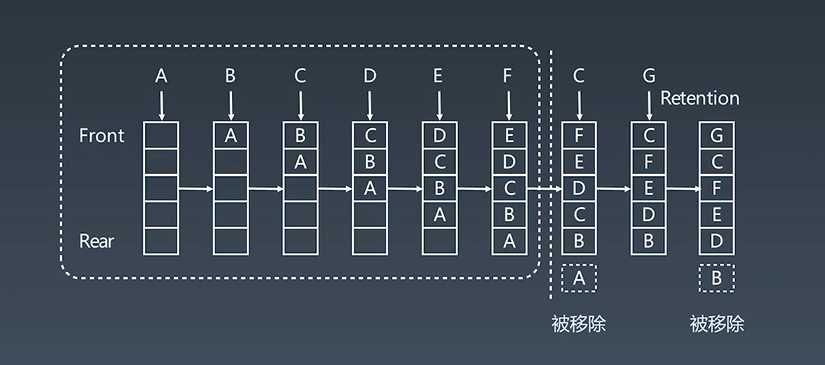
替换策略:
LFU - least frequently used
LRU - least recently used
如何基于链表实现 LRU 缓存淘汰算法?
维护一个有序单链表,越靠近链表尾部的结点是越早之前访问的。当有一个新的数据被访问时,从链表头开始顺序遍历链表。
①. 如果此数据之前已经被缓存在链表中了,遍历得到这个数据对应的结点,并将其从原来的位置删除,然后再插入到链表的头部。
②. 如果此数据没有在缓存链表中,又可以分为两种情况:
这样我们就用链表实现了一个 LRU 缓存。
m 缓存访问的时间复杂度是多少。因为不管缓存有没有满,都需要遍历一遍链表,所以这种基于链表的实现思路,缓存访问的时间复杂度为 O(n)。
可以继续优化这个实现思路,比如引入散列表(Hash table)来记录每个数据的位置,将缓存访问的时间复杂度降到 O(1)。
LRUCache Python
class LRUCache(object):
def __init__(self, capacity):
self.dic = collections.OrderedDict()
self.remain = capacity
def get(self, key):
if key not in self.dic:
return -1
v = self.dic.pop(key)
self.dic[key] = v # key as the newest one
return v
def put(self, key, value):
if key in
self.dic: self.dic.pop(key)
else:
if self.remain > 0:
self.remain -= 1
else: # self.dic is full
self.dic.popitem(last=False)
self.dic[key] = value
LRUCache Java
private Map<Integer, Integer> map;
public LRUCache(int capacity) {
map = new LinkedCappedHashMap<>(capacity);
}
public int get(int key) {
if (!map.containsKey(key)) {
return -1;
}
return map.get(key);
}
public void put(int key, int value) {
map.put(key, value);
}
private static class LinkedCappedHashMap<K, V> extends LinkedHashMap<K, V> {
int maximumCapacity;
LinkedCappedHashMap(int maximumCapacity) {
// initialCapacity代表map的容量, loadFactor代表加载因子, accessOrder默认false,如果要按读取顺序排序需要将其设为true
super(16, 0.75f, true);//default initial capacity (16) and load factor (0.75) and accessOrder (false)
this.maximumCapacity = maximumCapacity;
}
/* 重写 removeEldestEntry()函数,就能拥有我们自己的缓存策略 */
protected boolean removeEldestEntry(Map.Entry eldest) {
return size() > maximumCapacity;
}
}
借助散列表,我们可以把 LRU 缓存淘汰算法的时间复杂度降低为 O(1)
如何通过链表实现 LRU 缓存淘汰算法的。
我们需要维护一个按照访问时间从大到小有序排列的链表结构。因为缓存大小有限,当缓存空间 不够,需要淘汰一个数据的时候,我们就直接将链表头部的结点删除。
当要缓存某个数据的时候,先在链表中查找这个数据。如果没有找到,则直接将数据放到链表的 尾部;如果找到了,我们就把它移动到链表的尾部。因为查找数据需要遍历链表,所以单纯用链 表实现的 LRU 缓
存淘汰算法的时间复杂很高,是 O(n)。
实际上,我总结一下,一个缓存(cache)系统主要包含下面这几个操作:
这三个操作都要涉及“查找”操作,如果单纯地采用链表的话,时间复杂度只能是 O(n)。如果将散列表和链表两种数据结构组合使用,可以将这三个操作的时间复杂度都降低到 O(1)。
具体结构如下:
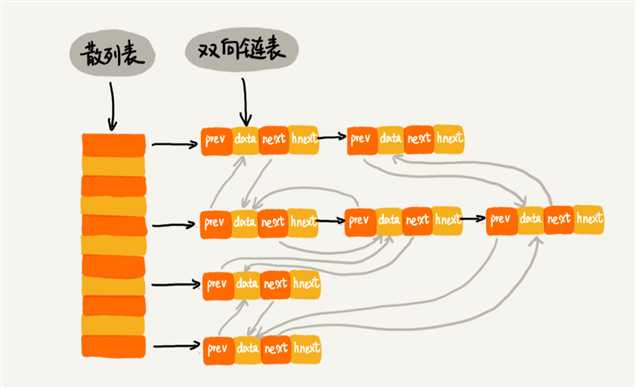
使用双向链表存储数据,链表中的每个结点处理存储数据(data)、前驱指针(prev)、 后继指针(next)之外,还新增了一个特殊的字段 hnext。这个 hnext 有什么作用呢?
因为我们的散列表是通过链表法解决散列冲突的,所以每个结点会在两条链中。一个链是刚刚我 们提到的双向链表,另一个链是散列表中的拉链。前驱和后继指针是为了将结点串在双向链表 中,hnext 指针是
为了将结点串在散列表的拉链中。
原文:https://www.cnblogs.com/shengyang17/p/13644143.html