今天在做2019中级软考题的时候,遇到一个N皇后问题;
搜索了一下,先了解了一下它的基本原理。在一个n*n的棋盘上,要求n个皇后所在行,列,以及对角线不能出现其他的皇后。
首先来说一下他的判断原理:用x[i]来描述i行的皇后所处的位置
不同行的皇后不在同一列:x[i]!=x[k]
不同行的皇后不在同一对角线 abs(x[i]-x[k])!=abs(i-k)
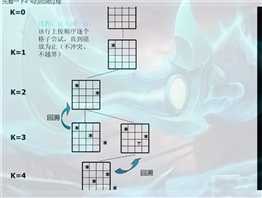
N皇后的判断方法用的是回溯法:!!!
回溯法(探索与回溯法)是一种选优搜索法,又称为试探法,按选优条件向前搜索,以达到目标。但当探索到某一步时,发现原先选择并不优或达不到目标,就退回一步重新选择,这种走不通就退回再走的技术为回溯法,而满足回溯条件的某个状态的点称为“回溯点”。
package com.javaTest.cn.nqueen; import java.util.Scanner; public class Nqueen { //皇后的个数 int n; //第几行的皇后放在哪一列 int[] x=new int[100]; //记录有多少种方案 int sum=0; public void output(int n){ System.out.println("第"+sum+"种方案为:"); for (int i = 1; i <= n; i++) { System.out.println("("+i+","+x[i]+")"); } } public boolean place(int k) { for (int j = 1; j < k; j++) { //判断给皇后使得否在同一列或者对角线上; if (x[j]==x[k]||Math.abs(x[j]-x[k])==Math.abs(j-k)) { return false; } } return true; } public void BackTrace(int t,int n) {//递归 if (t>n) {//如果t>n说明已经完成一次放置 sum++; output( n); }else { for (int i = 1; i <=n; i++) { x[t]=i; if (place(t)) {//可以放在i位置处,则继续搜索 BackTrace(t+1, n); } } } } public void BackTrace1(int n) {//非递归 int k; x[1]=0; k=1; while(k>=1) { x[k]+=1;//先放在第一个位置 while (x[k]<=n&&!(place(k))) {//当不能放时; x[k]++; } if (x[k]<=n) { if (k==n) { sum++; output(n); }else { //没有处理完,让k自加,处理下一个皇后 k++; x[k]=0; } }else {// 当前无法完成放置,则进行剪枝,回溯回去,回到第k-1步 k--; } } } public static void main(String[] args) { System.out.println("您需要测试的是多少个皇后?请输入!"); Scanner sc=new Scanner(System.in); int count=Integer.parseInt(sc.nextLine()); System.out.println(count+"皇后的放置方法为:"); Nqueen nqueen=new Nqueen(); //nqueen.BackTrace(count); nqueen.BackTrace(1, count); } }
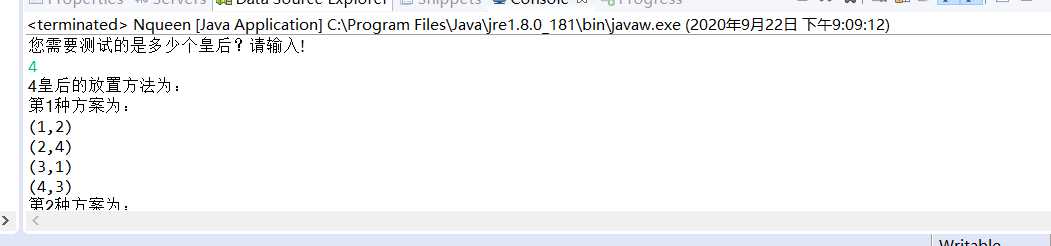
参考博客:链接
原文:https://www.cnblogs.com/moxihuishou/p/13714995.html